Educational Codeforces Round 139 (Rated for Div. 2)
Problem - 1766E - Codeforces
显然我们可以把0序列的贡献单独算: i*(n-i+1)
考虑只存在1,2,3的情况.
首先通过,观察到一个重要性质:
最多只有三种序列.
- 含有3或纯1或纯2型.
- 纯1或纯2型
- 纯2或纯1型
我们每次添加元素的操作,只跟上一个位置序列的最后一个元素有关
每个位置最多有3种类型的序列,所以每个位置的状态数是很有限的,这个很重要!
设 dp[i][j][k][l] 表示 以i为右端点的且当前序列状态为 (j,k,l) 的区间数量.
转移:
当前位置为 b[i], 枚举上一个位置的状态(j,k,l)
转移方程为:
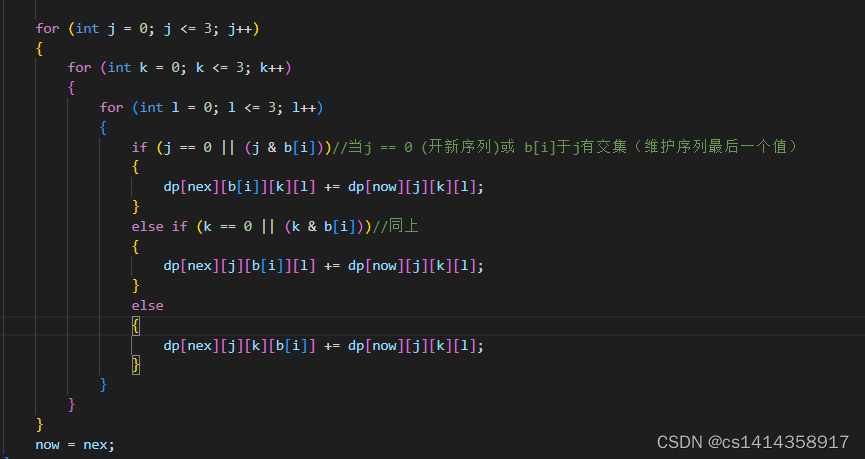
AC代码:
#include <bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
#define int long long
#define endl '\n'
#define bit(x) (1ll << x)
using namespace std;
const int N = 3 * 1e3 + 5;
const int inf = 1e16;
int dp[7][7][7][7];
void solve()
{
int n;
cin >> n;
vector<int> a(n + 1), b(n + 1);
int ans = 0;
for (int i = 1; i <= n; i++)
{
cin >> b[i];
}
int now = 0;
int nex = 0;
for (int i = 1; i <= n; i++)
{
dp[now][0][0][0]++;
if (b[i] == 0)
{
ans += i * (n - i + 1);//单独统计0序列的贡献,其他状态由上一个转移,没变
}
else
{
nex = now^1;
for (int j = 0; j <= 3; j++)
for (int k = 0; k <= 3; k++)
for (int l = 0; l <= 3; l++)
{
dp[nex][j][k][l] = 0;
}
for (int j = 0; j <= 3; j++)
{
for (int k = 0; k <= 3; k++)
{
for (int l = 0; l <= 3; l++)
{
if (j == 0 || (j & b[i]))//当j == 0 (开新序列)或 b[i]于j有交集(维护序列最后一个值)
{
dp[nex][b[i]][k][l] += dp[now][j][k][l];
}
else if (k == 0 || (k & b[i]))//同上
{
dp[nex][j][b[i]][l] += dp[now][j][k][l];
}
else
{
dp[nex][j][k][b[i]] += dp[now][j][k][l];
}
}
}
}
now = nex;
}
for (int j = 0; j <= 3; j++)
{
for (int k = 0; k <= 3; k++)
{
for (int l = 0; l <= 3; l++)
{
ans += dp[now][j][k][l] * ((j > 0 ? 1 : 0) + (k > 0 ? 1 : 0) + (l > 0 ? 1 : 0));
}
}
}
}
cout << ans << endl;
}
q
signed main()qq
{
/*ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);*/
int t = 1;
// cin >> t;
while (t--)
{
solve();
}
return 0;
}q