1. 题目描述

给你一个整数数组nums，请计算数组的中心位置，数组的中心位置是数组的一个下标，其左侧所有元素相乘的积等于右侧所有元素相乘的积。数组第一个元素的左侧积为1，最后一个元素的右侧积为1。如果数组有多个中心位置，应该返回最靠近左边的那一个，如果数组不存在中心位置，返回-1。

2. 输入描述

输入只有一行，给出N个正整数用空格分隔，nums = 2 5 3 6 5 6

1 <= nums.length <= 1024

1 <= nums[i] <= 10

3. 输出描述

3

4. Java算法源码

/**
 * 计算数组的中心位置，数组的中心位置是数组的一个下标，其左侧所有元素相乘的积等于右侧所有元素相乘的积。
 */
public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int[] nums = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();

    int n = nums.length;
    // 中间坐标
    int middle = n / 2;
    boolean leftFlag = true;
    boolean rightFlag = false;
    List<Integer> list = new ArrayList<Integer>();
    while (true) {
        // 左边数的乘积
        int left_multi = 1;
        for (int i = 0; i < middle; i++) {
            left_multi = left_multi * nums[i];
        }
        
        // 右边数的乘积
        int right_multi = 1;
        for (int i = middle + 1; i < nums.length; i++) {
            right_multi = right_multi * nums[i];
        }

        //若左右两边乘积相同，则保存
        if (left_multi == right_multi) {
            list.add(middle);
        }

        if (leftFlag) {
            if (middle > 1) {
                middle--;
                continue;
            } else {
                // 左边完成，将右边开关打开，并重置初始中心下标，准备往右边移动
                leftFlag = false;
                rightFlag = true;
                middle = n / 2;
            }
        }

        if (rightFlag) {
            if (middle < nums.length - 2) {
                middle++;
            } else {
                //右边也已完成，工作完成，跳出循环
                break;
            }
        }
    }

    // 如果数组有多个中心位置，应该返回最靠近左边的那一个，如果数组不存在中心位置，返回-1。
    if(list.size() == 0){
        System.out.println(-1);
    }else{
        Collections.sort(list);
        System.out.println(list.get(0));
    }
}

5. 测试

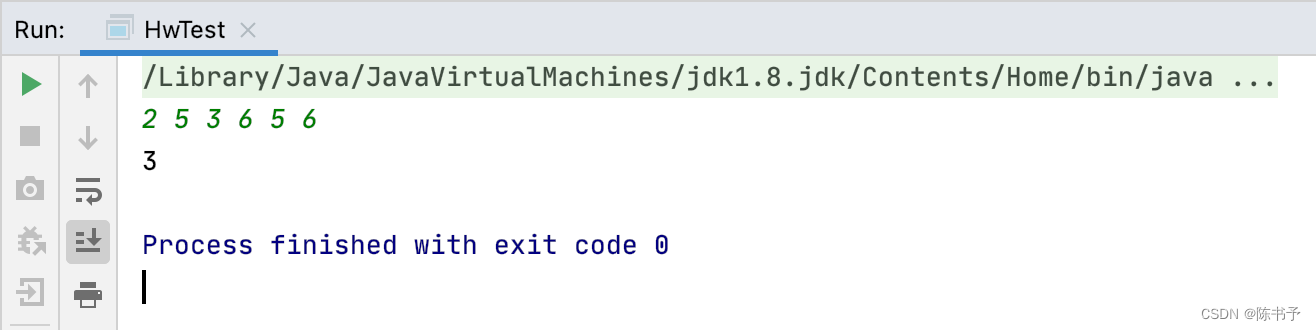
在这里插入图片描述

6.解题思路

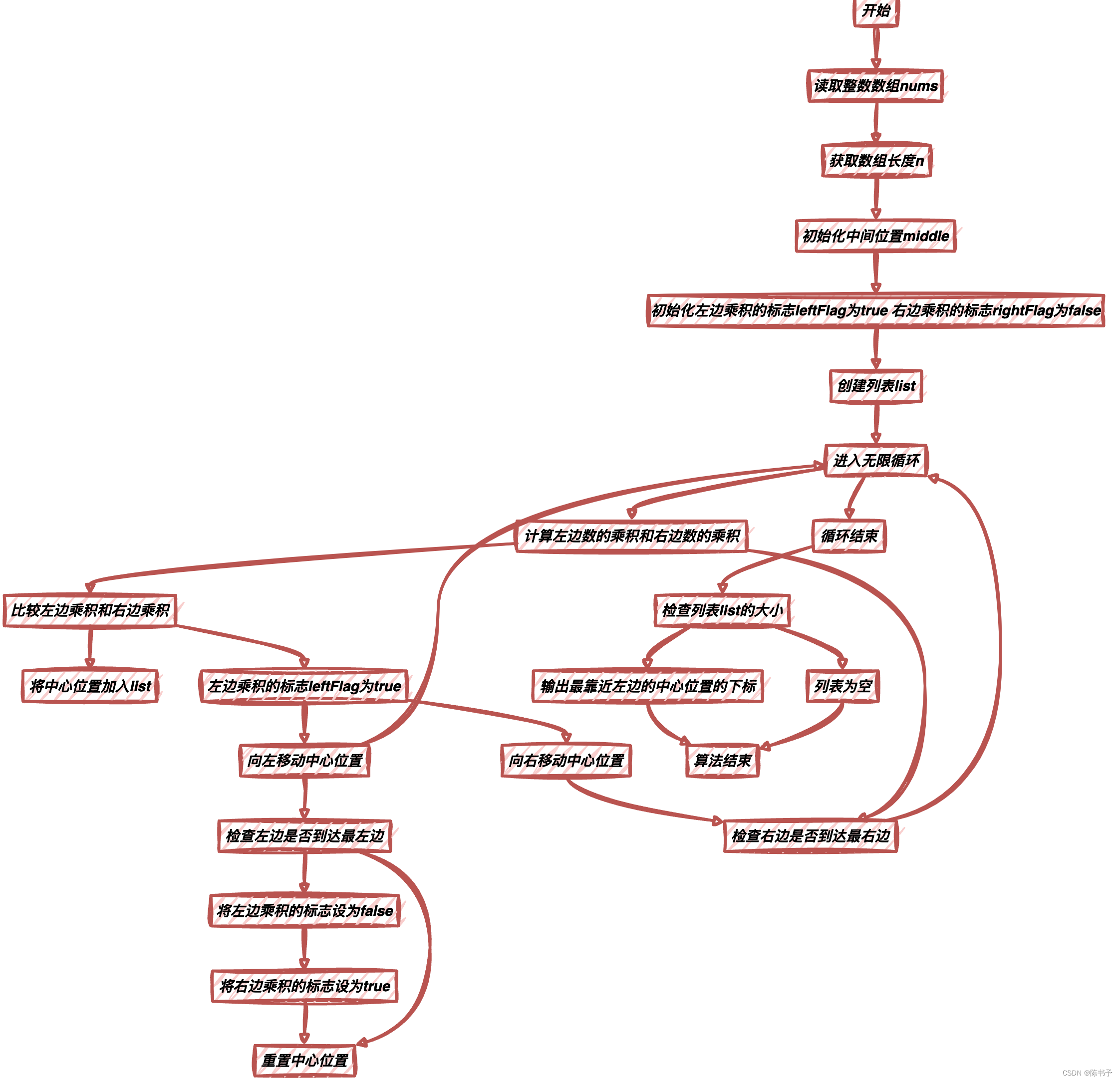
在这里插入图片描述

读取输入的整数数组nums。
获取数组的长度n。
初始化中间位置middle为n / 2。
初始化左边乘积的标志leftFlag为true，右边乘积的标志rightFlag为false。
创建一个列表list，用于存储中心位置的下标。
进入一个无限循环，直到找到中心位置或完成搜索。
在循环中，计算左边数的乘积和右边数的乘积，并将它们进行比较。
如果左边乘积等于右边乘积，将当前中心位置加入到list中。
如果左边乘积的标志leftFlag为true，将中心位置向左移动一位，如果已经到达数组的最左边，则将左边乘积的标志设为false，右边乘积的标志设为true，并将中心位置重置为n / 2。
如果右边乘积的标志rightFlag为true，将中心位置向右移动一位，如果已经到达数组的最右边，则退出循环。
循环结束后，检查列表list的大小。
如果列表为空，表示数组不存在中心位置，输出-1。
否则，将列表list排序，并输出最靠近左边的中心位置的下标。