图

图的基本概念

图的定义

种类

图的抽象数据类型

图的基本术语

1. 端点和邻接点

2. 顶点的度、入度和出度

公式

3. 完全图

4. 稠密图、稀疏图

5. 子图

6. 路径和路径长度

7. 回路或环

8. 连通、连通图和连通分量

练习

9. 强连通图和强连通分量

在一个图中找强连通分量的方法

例题

10. 权和网

图的存储结构和基本运算算法

图的存储表示

邻接矩阵存储方法

//定义最大顶点数为100
#define MaxVertexNum 100
typedef struct {
    char Vex[MaxVertexNum];   //顶点数组，存储顶点名称
    int Edge[MaxVertexNum][MaxVertexNum];   //邻接矩阵，存储顶点之间的边
    int vexNum,arcNum;    //顶点个数和边数
} MGraph;

演示

特点

邻接表存储方法

图的邻接表存储方法是一种顺序分配与链式分配相结合的存储方法

//定义最大顶点数为100
#define MaxVertexNum 100
//邻接表存储结构中的边结点
typedef struct ArcNode{
    int adjVex;   //记录该边依附的顶点在顶点数组中的下标
    struct ArcNode *next;   //指向下一个边结点
} ArcNode;
//邻接表存储结构中的顶点结点
typedef struct VNode{
    char data;   //顶点数据
    ArcNode *first;   //指向第一条依附该顶点的边结点
} VNode, AdjList[MaxVertexNum];
//邻接表存储结构
typedef struct {
    AdjList vertices;   //邻接表
    int vexNum,arcNum;   //存储顶点个数和边数
} ALGraph;

演示

特点

十字链表存储有向图

邻接多重表存储无向图

图的遍历

概念

方法

图的遍历有两种基本方法：深度优先搜索（Depth First Search，简称DFS）和广度优先搜索（Breadth First Search，简称BFS）。

深度优先遍历算法

过程

演示

广度优先遍历算法

过程

演示

DFS和BFS的差别

生成树和最小生成树

生成树

概念

如果在一棵生成树上添加一条边，必定构成一个环。

深度优先生成树

广度优先生成树

一个连通图的生成树不一定是唯一的。

最小生成树

概念

例

非连通图和生成树

【数据结构算法】图解prime算法和Kruskal算法（最短路径问题）

最小生成树算法——Prime算法、kruskal算法

普里姆算法

克鲁斯卡尔算法

最短路径

路径的概念

从一个顶点到其余各顶点的最短路径（Dijkstra算法）

求解思路

过程

算法设计

算法演示

Dijkstra算法不适合负权值的情况

每对顶点之间的最短路径（Floyd算法）

算法：迭代（递推）思路

算法设计

算法演示

有向无环图及其应用

第七章-图（6）有向无环图及其应用-拓扑排序

第七章-图（6）有向无环图及其应用-关键路径

有向无环图的定义

• 有向无环图（DAG，Directed Acyclic Graph）是图论中的一种特殊的有向图，它没有任何从某个顶点出发经过若干条边回到该顶点的路径，也就是说，它没有环。
• 有向无环图可以用来表示一些具有优先关系或依赖关系的问题，例如工程项目的进度安排、表达式的计算、编译器的优化等。
• 有向无环图可以用邻接表或邻接矩阵来存储，其中每个顶点可以用一个入度（指向该顶点的边的数量）和一个出度（从该顶点出发的边的数量）来描述。

例

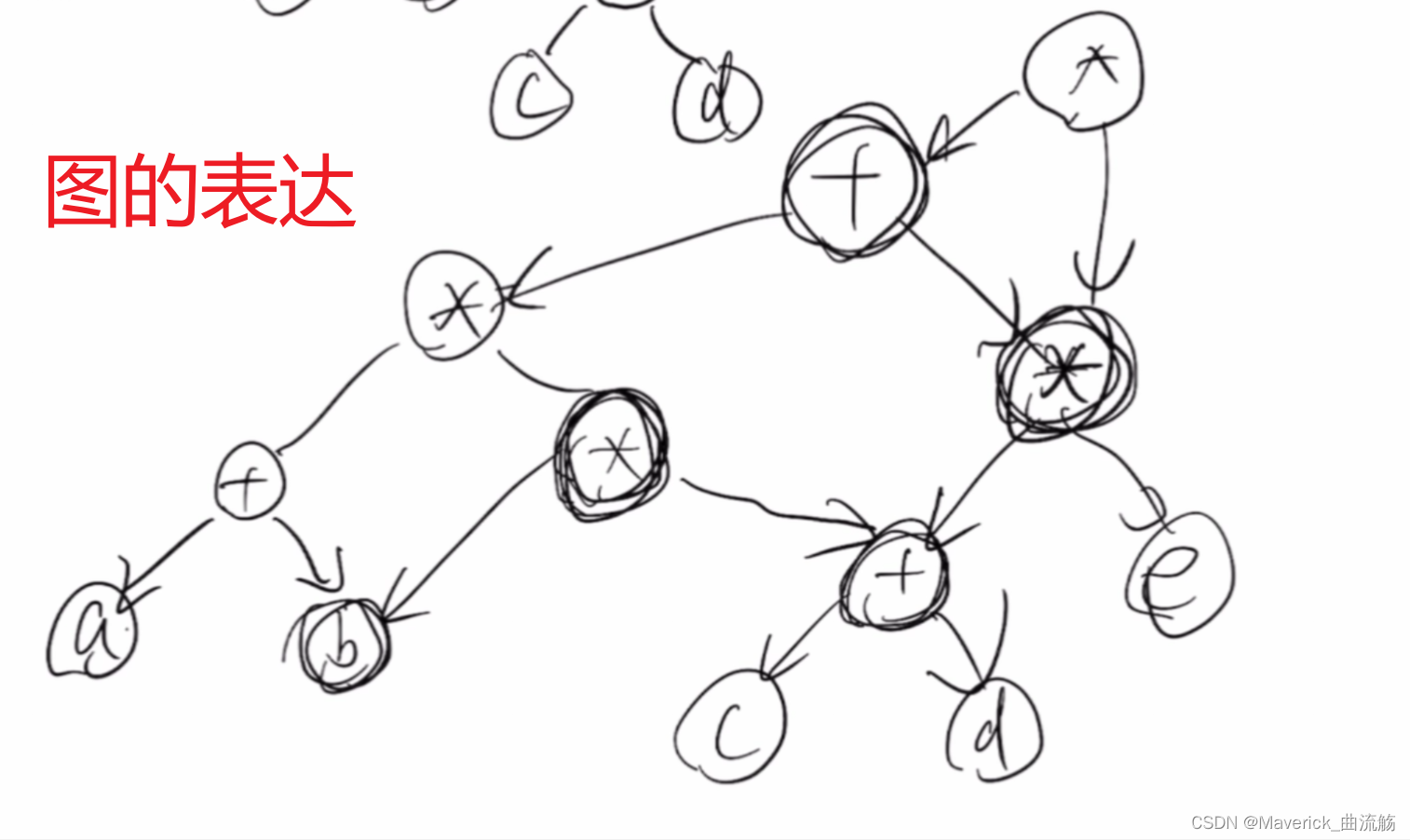
AOV网

AOV网（边是有向边，应用：拓扑排序）、AOE网（边是带权有向边，应用：关键路径）：最早和最晚时刻一致的活动（有向边）是关键路径中的活动

AOV和AOE之间的区别和联系

• AOV网（Activity On Vertex Network）是一种用顶点表示活动，用弧表示活动之间的优先关系的有向图，它可以用来表示一些具有偏序关系或依赖关系的问题，例如工程项目的进度安排、课程的选修顺序等。
• AOV网中的顶点表示一个活动，它可以是一个具体的任务或一个抽象的概念，它有一个开始时间和一个结束时间，以及一个持续时间。
• AOV网中的弧表示一个活动之间的优先关系，它指示了哪些活动必须在另一些活动之前完成，它可以有一个权值，表示两个活动之间的间隔时间。
• AOV网中没有环路，即不存在从某个顶点出发经过若干条弧回到该顶点的路径，否则就会出现矛盾或死锁。

有向无环图的拓扑排序

【数据结构】AOV网——拓扑排序

1. 从图中选择一个没有前驱的顶点输出。
2. 从图中删除该顶点和所有以他为顶点的边。
3. 重复第一，二步，直到图为空，或者不存在没有前驱的顶点。

AOE网

AOV网(拓扑排序)和AOE网

[关键路径（AOE）网 通俗易懂](关键路径（AOE）网 通俗易懂 - 知乎 (zhihu.com))

• AOE网（Activity On Edge Network）是一种用边表示活动，用顶点表示事件，用边上的权值表示活动持续的时间的有向图，它可以用来表示一些具有时间限制或工期要求的问题，例如工程项目的进度安排、任务的优先级等。
• AOE网中的边表示一个活动，它可以是一个具体的任务或一个抽象的概念，它有一个开始事件和一个结束事件，以及一个持续时间。
• AOE网中的顶点表示一个事件，它是所有指向它的边所代表的活动均已完成的状态，它有一个最早发生时间和一个最迟发生时间，以及一个时差。
• AOE网中没有环路，即不存在从某个顶点出发经过若干条边回到该顶点的路径，否则就会出现矛盾或死锁。
• AOE网中有一个入度为0的顶点称为源点或始点，表示一个工程的开始；有一个出度为0的顶点称为汇点或终点，表示一个工程的结束。
• AOE网可以用邻接表或邻接矩阵来存储，其中每个顶点可以用一个入度（指向该顶点的边的数量）和一个出度（从该顶点出发的边的数量）来描述。

AOE网的关键路径

【数据结构】AOE网——关键路径

• 关键路径（Critical Path）是一种对AOE网中所有边进行排序的方法，使得对于网中任意一条有向边<u,v>，边u在排序中都出现在边v之前。
• 关键路径可以用来检查一个有向图是否有环，也可以用来确定一个工程项目的最早开始时间和最晚开始时间。
• 关键路径是指在AOE网中从源点到汇点路径最长的路径。这里的路径长度是指路径上各个活动持续时间之和。
• 关键路径上的活动是关键活动，它们是决定整个工程工期的关键因素，即通过加快关键活动来缩短整个工程的工期。
• 关键路径上的事件是关键事件，它们是决定整个工程进度安排的关键节点，即通过调整关键事件来优化整个工程的进度安排。
• 关键路径并不唯一，即关键路径可能有多条。且对于有几条关键路径的网，只提高一条关键路径上的关键活动并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。

关键路径算法

• 关键路径算法（Critical Path Method）是一种求解AOE网中关键路径和关键活动的算法，它主要利用了以下几个参数：
  • 事件vk 的最早发生时间ve(k) —— 它是从源点v1到某个顶点vk 的最长路径长度。它决定了之后的活动能够开工的最早时间。
  • 事件vk 的最迟发生时间vl(k) —— 它是指在不推迟整个工期的前提下，该事件最迟必须发生的时间。
  • 活动ai 的最早开始时间e(i) —— 它是该活动的起点表示的事件的最早发生时间。
  • 活动ai 的最迟开始时间l(i) —— 它是该活动的终点表示的事件的最迟发生时间减去该活动所需时间之差。
  • 活动ai 的总时差t(i) —— 它是该活动最迟开始时间与最早开始时间之差。如果总时差为0，则该活动为关键活动。
• 关键路径算法主要分为以下几个步骤：
  • 计算每个事件（顶点）最早发生时间ve(k) 和最迟发生时间vl(k)：
    • ve(源点) = 0
    • ve(k) = max {ve(j) + cost(j,k)}
    • vl(汇点) = ve(汇点)
    • vl(k) = min {vl(j) - cost(k,j)}
  • 计算每个活动（边）最早开始时间e(i) 和最迟开始时间l(i)：
    • e(i) = ve(起点)
    • l(i) = vl(终点) - cost(起点,终点)
  • 确定关键路径和关键活动：
    • 如果某条路径上所有活动总时差都为0，则该路径为关键路径；如果某个活动总时差为0，则该活动为关键活动。
    • 关键路径和关键活动可能不止一条或一项。