目录
1. 概念
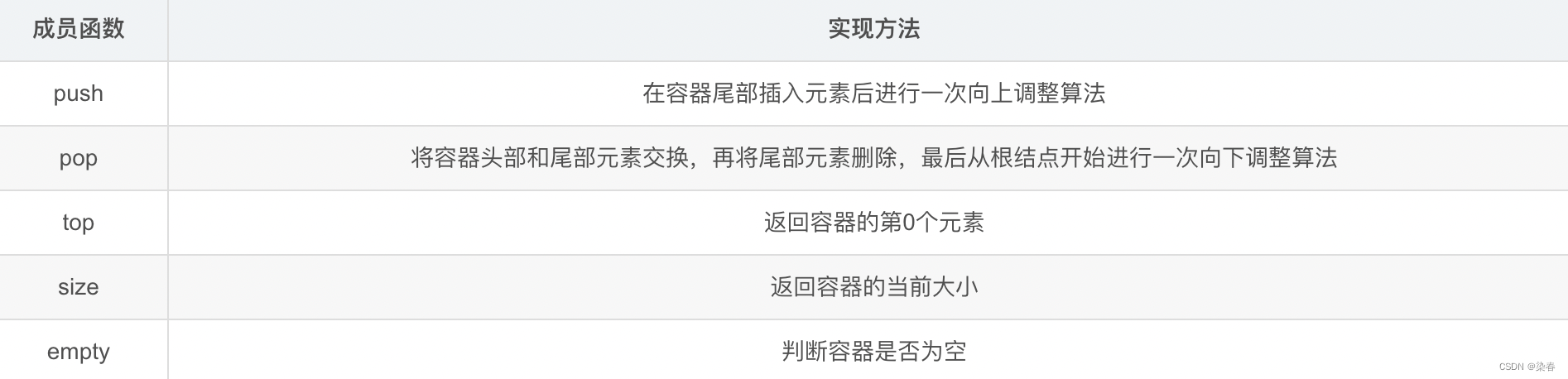
2. 常用的栈的方法
2.1 方法
2.2 代码
3. 自己实现栈
3.1 构造MyStack
3.2 push()
3.3 ensureCapacity()
3.4 pop()
3.5 peek()
3.6 empty()
3.7 szie()
4. 栈的应用
1. 概念
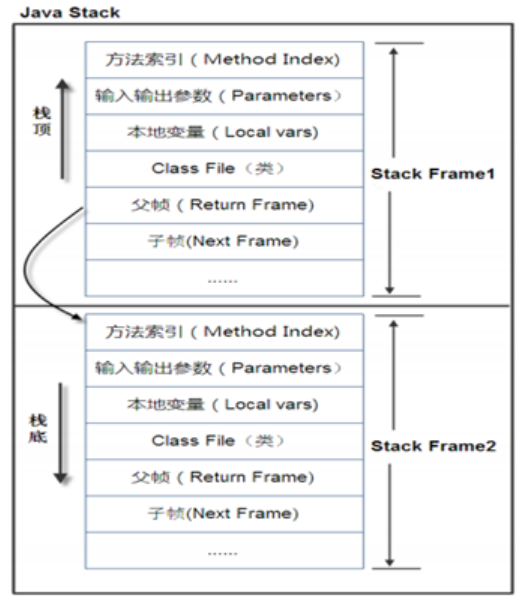
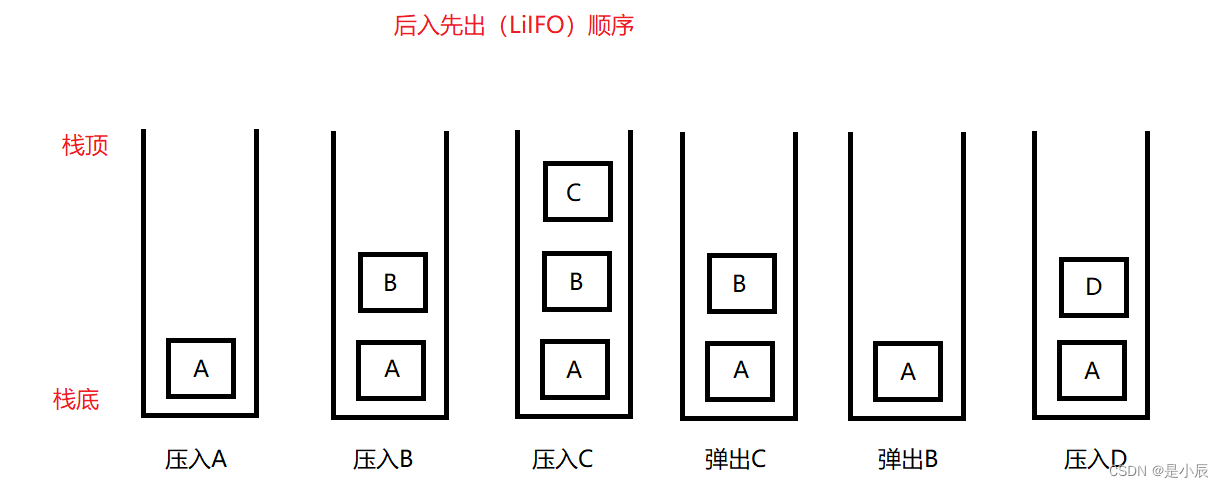
栈(Stack)是一种数据结构,是一种特殊的线性表,它是按照后进先出(Last-In-First-Out, LIFO)原则工作的线性数据结构。栈中的插入和删除元素的操作只能在栈顶进行,因此栈也被称为“后进先出表”。栈可以用数组或链表实现。
栈最基本的操作是:入栈(Push)、出栈(Pop)和获取栈顶元素(Top)。其中,入栈操作将元素放到栈顶,出栈操作将栈顶元素移除并返回其值,获取栈顶元素则是获取栈顶元素的值但是不移除栈顶元素。
另外,栈还有一些其他的常用操作,如:判断栈是否为空(IsEmpty)、获取栈中元素的个数(Size)、清空栈中的所有元素(Clear)等。
2. 常用的栈的方法
2.1 方法
| 方法 | 功能 |
|---|---|
| push() | 在栈顶插入元素 |
| pop() | 删除栈顶元素,并返回该元素的值。如果栈为空,则抛出EmptyStackException异常 |
| peek() | 返回该元素的值。如果栈为空,则抛出EmptyStackException异常 |
| empty() | 如果栈为空返回true,或者返回false |
| size() | 返回栈内元素个数 |
2.2 代码
public static void main(String[] args) {
Stack<Character> stack = new Stack<>();
//插入A B C
stack.push('A');
stack.push('B');
stack.push('C');
System.out.println(stack.size());//获得栈中元素个数,打印 3
System.out.println(stack.pop());//删除并获得栈顶元素 C
System.out.println(stack.pop());//删除并获得栈顶元素 B
stack.push('D');//栈顶插入D
System.out.println(stack.empty());
}
注意:
- 方法push(),pop(),peek()都是在栈顶执行插入,删除以及检索操作。isEmpty()和size()是标准的集合方法。
- 栈顶操作的pop(),peek()的执行条件是栈不为空。
3. 自己实现栈
3.1 构造MyStack
Stack是动态顺序表,可以使用数组来实现,则我们需要创建一个数组,还可以用一个创建一个变量记录栈内元素大小。
public class MyStack {
public int[] elem;
public int size = 0;
public MyStack(){
elem = new int[10];
}
//...
}3.2 push()
先进行判断栈的容量大小是否足够,不够进行栈的扩容,在进行压栈,反之,直接压栈,并将记录栈的大小的size加1;
//入栈、压栈
public void push(int val){
if(size == elem.length){
ensureCapacity();
}
elem[size] = val;
size++;
}3.3 ensureCapacity()
栈中的元素个数不小于容量时,要对容量进行扩容,就是将栈中的元素克隆到更大的数组中。
private void ensureCapacity() {
elem = Arrays.copyOf(elem,2 * elem.length);
}
3.4 pop()
出栈的时候要进行判断栈是否为空,如果栈为空,抛出EmptyStackException异常,反之,将栈顶元素删除并抛出,记录栈元素大小的size 减1;
public int pop(){
if(size == 0 ){
throw new EmptyStackException();
}
return elem[--size];
}3.5 peek()
只需要把栈顶元素返回,要进行判断栈是否为空,如果栈为空,抛出EmptyStackException异常。
//获得栈顶
public int peek(){
if(size == 0){
throw new EmptyStackException();
}
int key = size - 1;
return elem[key];
}3.6 empty()
判断size大小,szie = 0; 则返回true,反之false;
//检查栈是否为空
public boolean empty(){
return size == 0;
}3.7 szie()
直接返回size大小;
//栈内元素的个数
public int size(){
return size;
}4. 栈的应用
- 改变元素的序列
- 将递归转化为循环
- 括号匹配
- 逆波兰表达式求值
- 最小栈
这些都是较重要的应用,篇幅较大,我就放在了下篇博客,喜欢的可以点我主页查看。