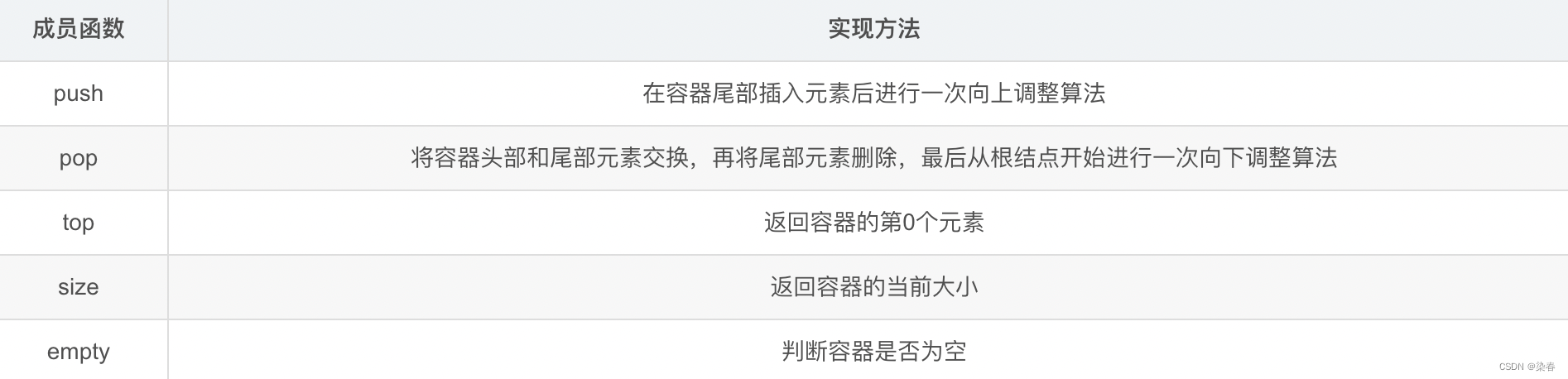
priority_queue的使用
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中的元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。
注意: 默认情况下priority_queue是大堆。
priority_queue的定义方式
方式一: 使用vector作为底层容器,内部构造大堆结构。
priority_queue<int, vector<int>, less<int>> q;
方式二: 使用vector作为底层容器,内部构造小堆结构。
priority_queue<int, vector<int>, greater<int>> q;
方式三: 不指定底层容器和内部需要构造的堆结构。
priority_queue<int> q;
注意: 此时默认使用vector作为底层容器,内部默认构造大堆结构。
priority_queue各个接口的使用
priority_queue的各个成员函数及其功能如下:
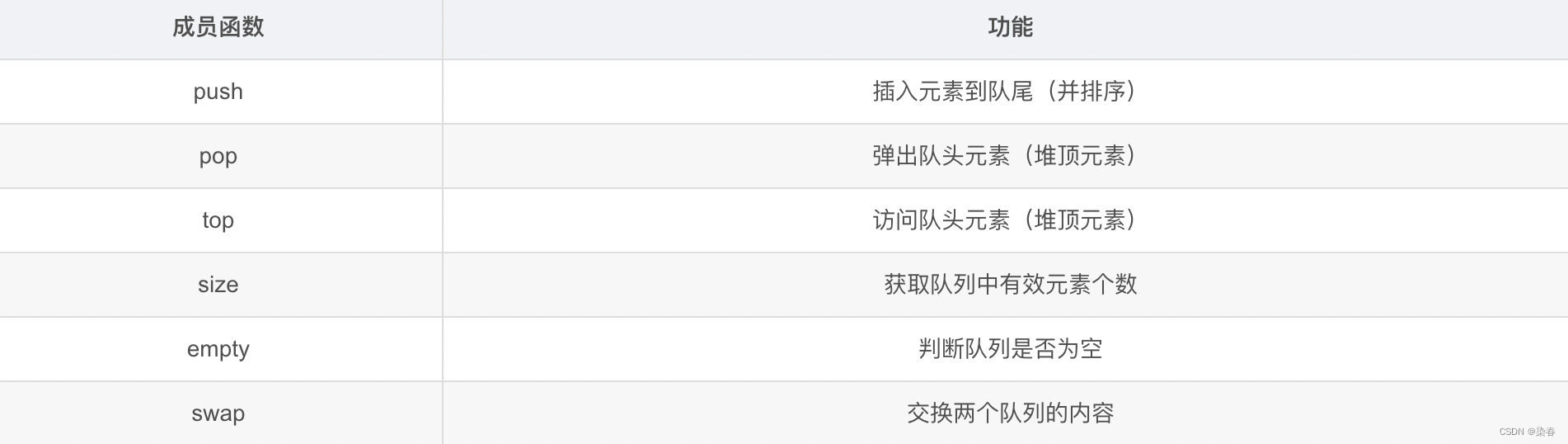
示例:
#include <iostream> #include <functional> #include <queue> using namespace std; int main() { priority_queue<int> q; q.push(4); q.push(6); q.push(5); q.push(2); q.push(3); q.push(1); while (!q.empty()) { cout << q.top() << " "; q.pop(); } cout << endl; //6 5 4 3 2 1 return 0; }
priority_queue的模拟实现
priority_queue的底层实际上就是堆结构,实现priority_queue之前,我们先认识两个重要的堆算法。(下面这两种算法我们均以大堆为例)
堆的向上调整算法
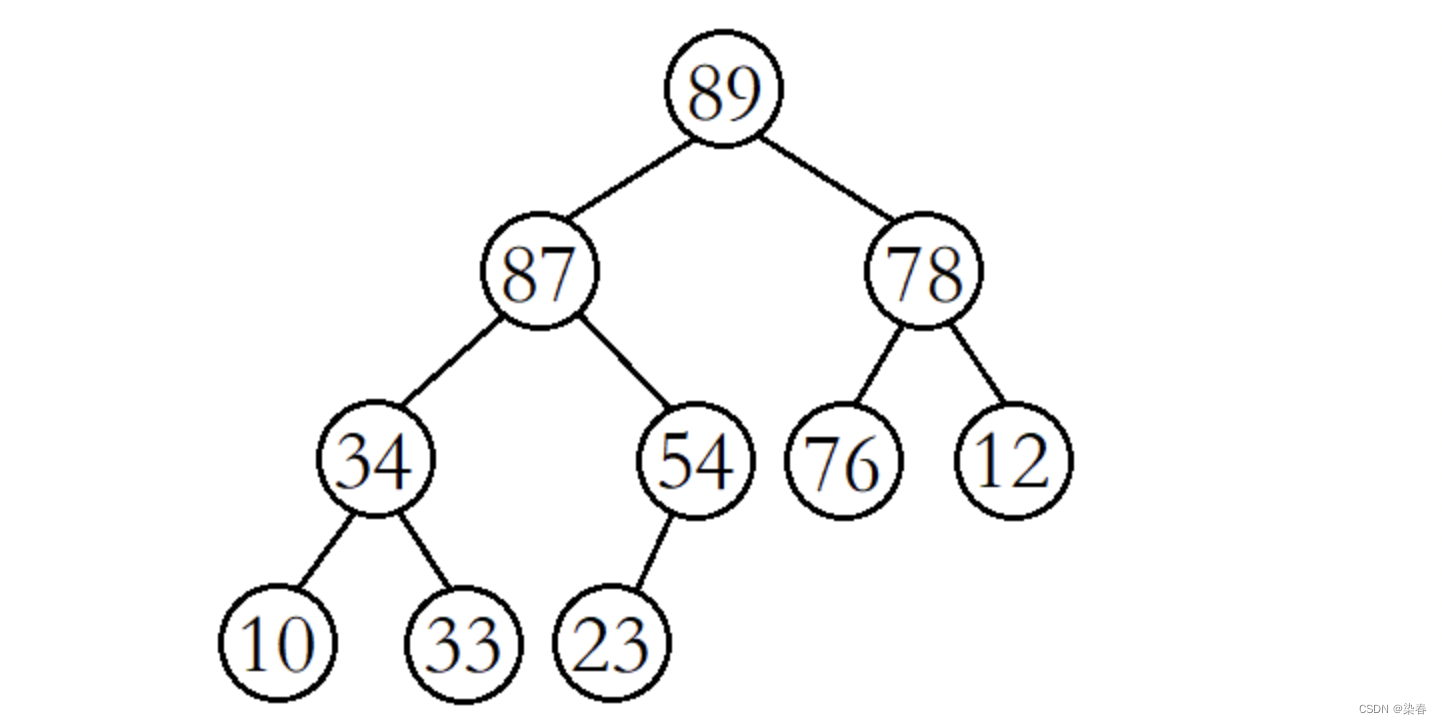
以大堆为例,堆的向上调整算法就是在大堆的末尾插入一个数据后,经过一系列的调整,使其仍然是一个大堆。
调整的基本思想如下:
1、将目标结点与其父结点进行比较。
2、若目标结点的值比父结点的值大,则交换目标结点与其父结点的位置,并将原目标结点的父结点当作新的目标结点继续进行向上调整;若目标结点的值比其父结点的值小,则停止向上调整,此时该树已经是大堆了。
例如,现在我们在该大堆的末尾插入数据88。
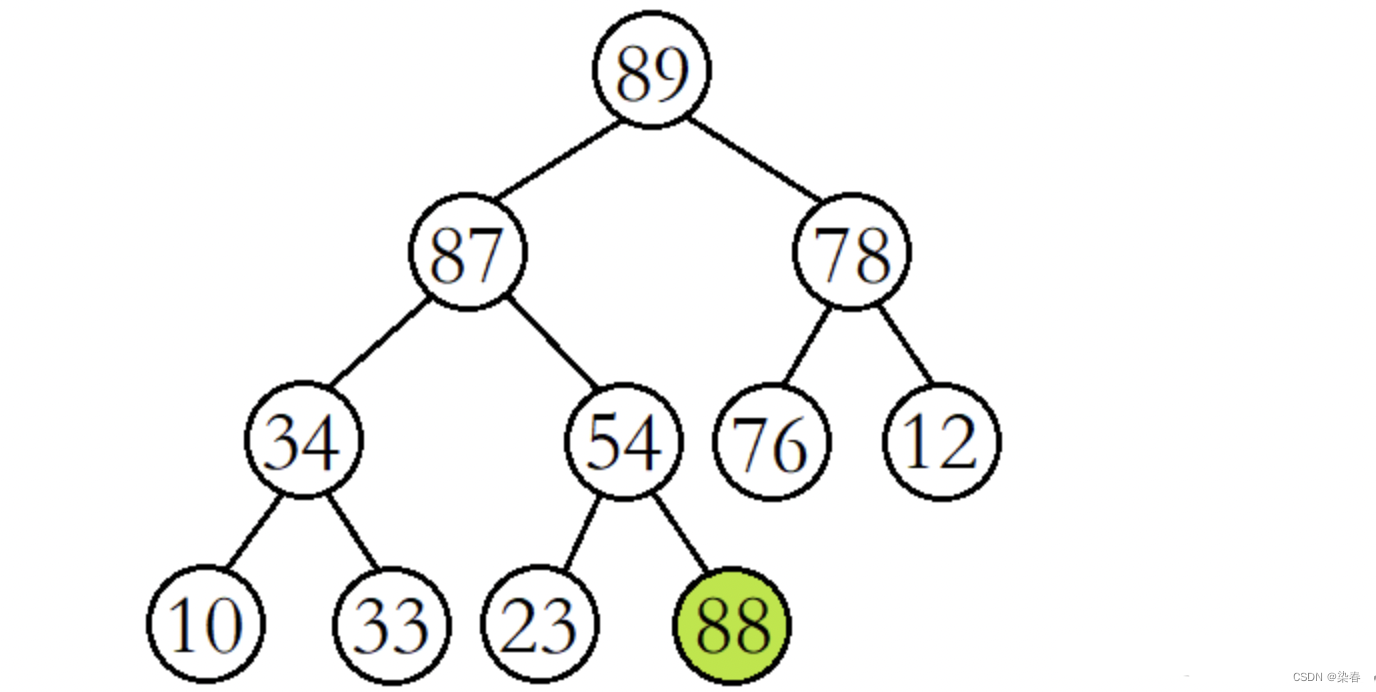
我们先将88与其父结点54进行比较,发现88比其父结点大,则交换父子结点的数据,并继续进行向上调整。
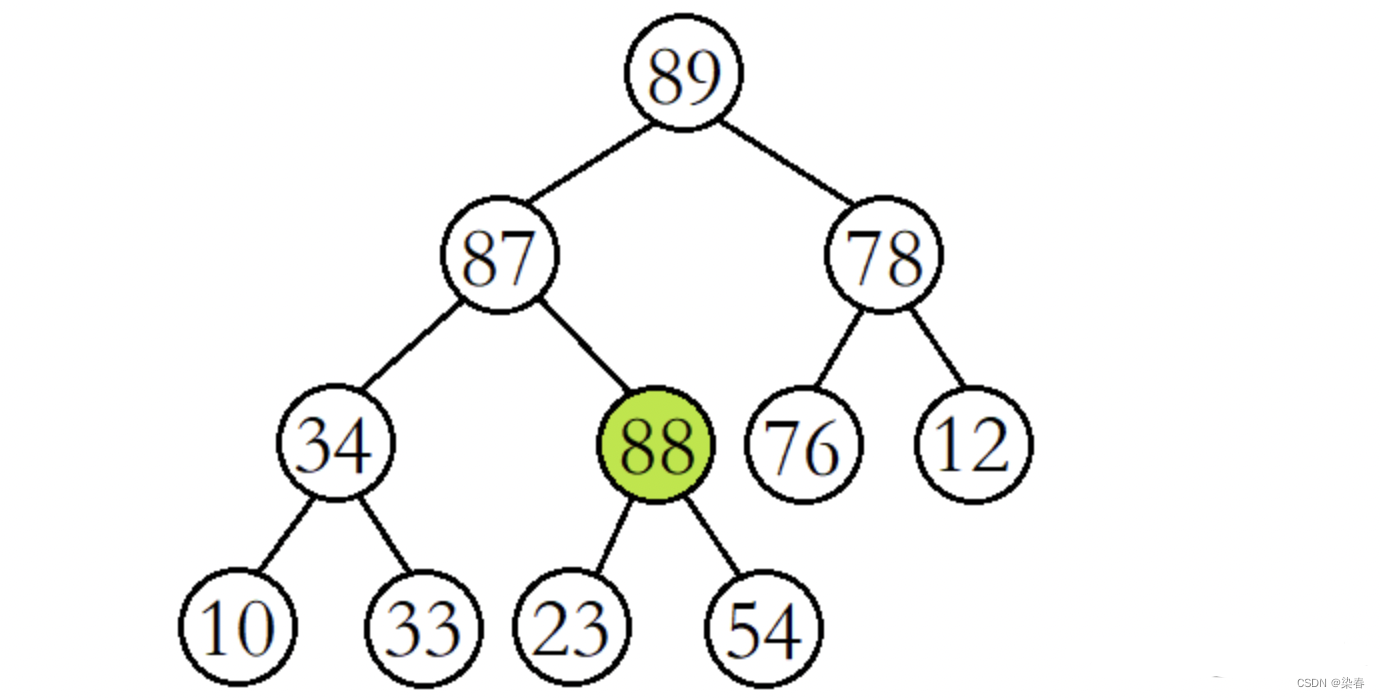
此时将88与其父结点87进行比较,发现88还是比其父结点大,则继续交换父子结点的数据,并继续进行向上调整。

这时再将88与其父结点89进行比较,发现88比其父结点小,则停止向上调整,此时该树已经就是大堆了。

堆的向上调整算法代码:
//堆的向上调整(大堆) void AdjustUp(vector<int>& v, int child) { int parent = (child - 1) / 2; //通过child计算parent的下标 while (child > 0)//调整到根结点的位置截止 { if (v[parent] < v[child])//孩子结点的值大于父结点的值 { //将父结点与孩子结点交换 swap(v[child], v[parent]); //继续向上进行调整 child = parent; parent = (child - 1) / 2; } else//已成堆 { break; } } }
堆的向下调整算法
以大堆为例,使用堆的向下调整算法有一个前提,就是待向下调整的结点的左子树和右子树必须都为大堆。
调整的基本思想如下:
1、将目标结点与其较大的子结点进行比较。
2、若目标结点的值比其较大的子结点的值小,则交换目标结点与其较大的子结点的位置,并将原目标结点的较大子结点当作新的目标结点继续进行向下调整;若目标结点的值比其较大子结点的值大,则停止向下调整,此时该树已经是大堆了。
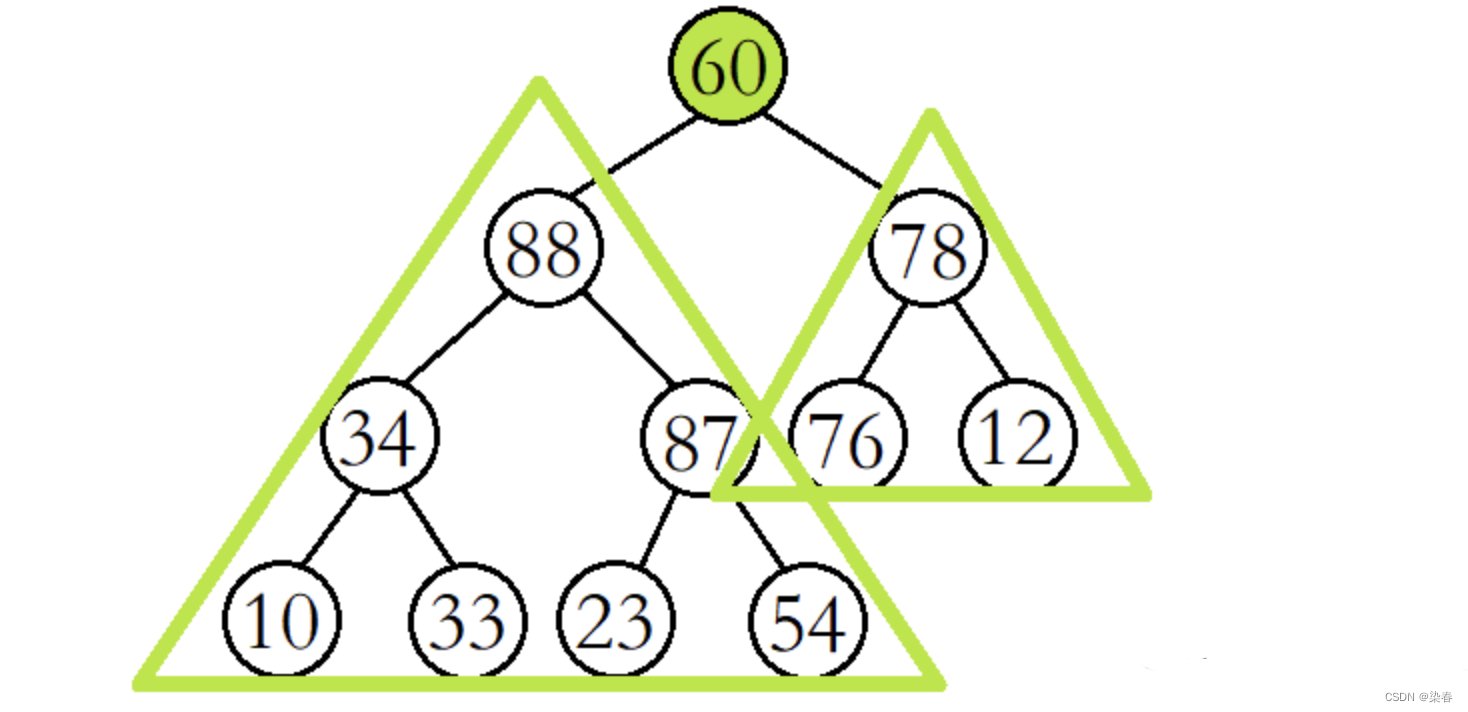
例如,将该二叉树从根结点开始进行向下调整。(此时根结点的左右子树已经是大堆)
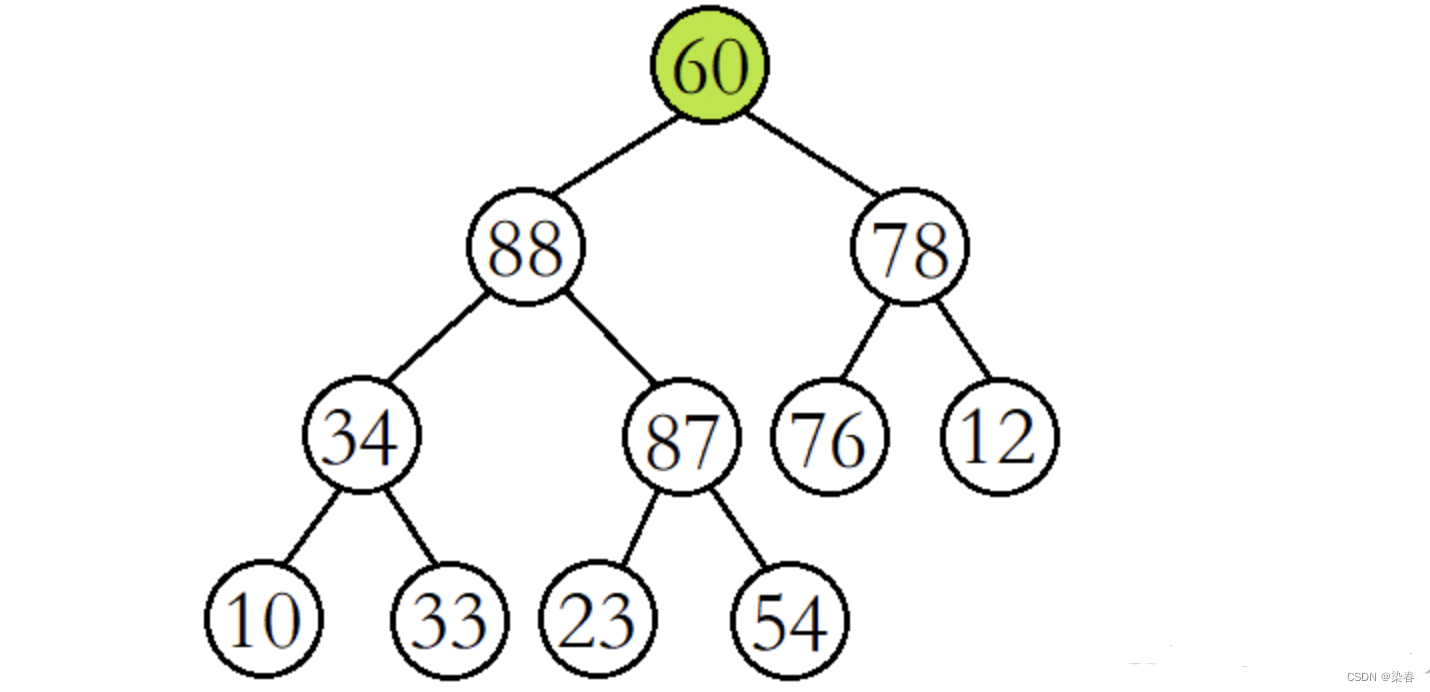
将60与其较大的子结点88进行比较,发现60比其较大的子结点小,则交换这两个结点的数据,并继续进行向下调整。
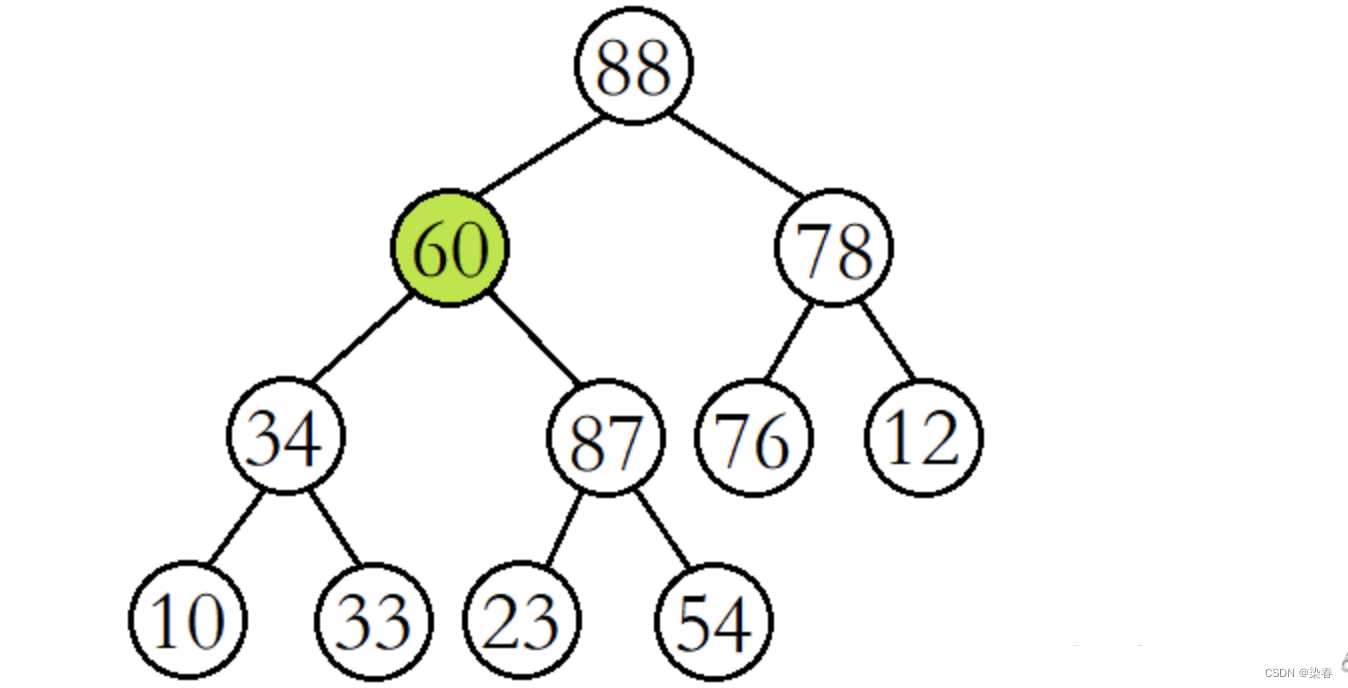
此时再将60与其较大的子结点87进行比较,发现60比其较大的子结点小,则再交换这两个结点的数据,并继续进行向下调整。

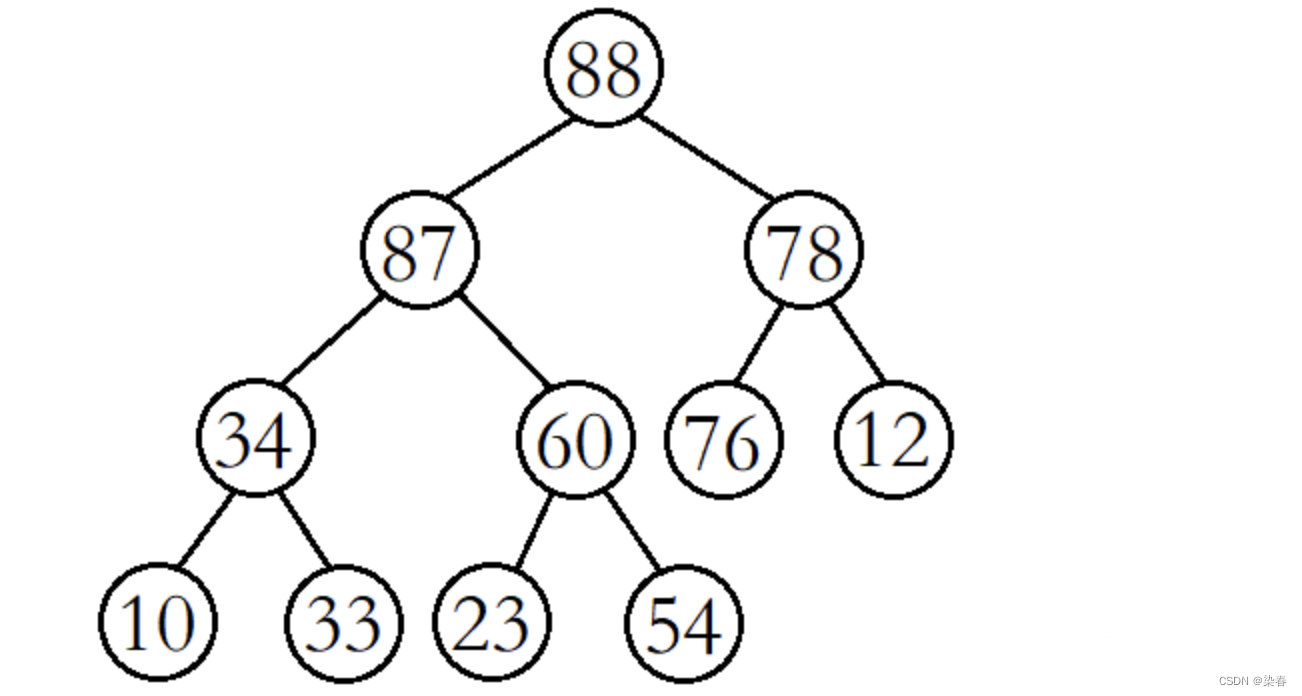
这时再将60与其较大的子结点54进行比较,发现60比其较大的子结点大,则停止向下调整,此时该树已经就是大堆了。
堆的向下调整算法代码:
//堆的向下调整(大堆) void AdjustDown(vector<int>& v, int n, int parent) { //child记录左右孩子中值较大的孩子的下标 int child = 2 * parent + 1;//先默认其左孩子的值较大 while (child < n) { if (child + 1 < n&&v[child] < v[child + 1])//右孩子存在并且右孩子比左孩子还大 { child++;//较大的孩子改为右孩子 } if (v[parent] < v[child])//左右孩子中较大孩子的值比父结点还大 { //将父结点与较小的子结点交换 swap(v[child], v[parent]); //继续向下进行调整 parent = child; child = 2 * parent + 1; } else//已成堆 { break; } } }
priority_queue的模拟实现
只要知道了堆的向上调整算法和堆的向下调整算法,priority_queue的模拟实现就没什么困难了。
priority_queue的模拟实现代码:
namespace zhc //防止命名冲突 { //比较方式(使内部结构为大堆) template<class T> struct less { bool operator()(const T& x, const T& y) { return x < y; } }; //比较方式(使内部结构为小堆) template<class T> struct greater { bool operator()(const T& x, const T& y) { return x > y; } }; //优先级队列的模拟实现 template<class T, class Container = vector<T>, class Compare = less<T>> class priority_queue { public: //堆的向上调整 void AdjustUp(int child) { int parent = (child - 1) / 2; //通过child计算parent的下标 while (child > 0)//调整到根结点的位置截止 { if (_comp(_con[parent], _con[child]))//通过所给比较方式确定是否需要交换结点位置 { //将父结点与孩子结点交换 swap(_con[child], _con[parent]); //继续向上进行调整 child = parent; parent = (child - 1) / 2; } else//已成堆 { break; } } } //插入元素到队尾(并排序) void push(const T& x) { _con.push_back(x); AdjustUp(_con.size() - 1); //将最后一个元素进行一次向上调整 } //堆的向下调整 void AdjustDown(int n, int parent) { int child = 2 * parent + 1; while (child < n) { if (child + 1 < n&&_comp(_con[child], _con[child + 1])) { child++; } if (_comp(_con[parent], _con[child]))//通过所给比较方式确定是否需要交换结点位置 { //将父结点与孩子结点交换 swap(_con[child], _con[parent]); //继续向下进行调整 parent = child; child = 2 * parent + 1; } else//已成堆 { break; } } } //弹出队头元素(堆顶元素) void pop() { swap(_con[0], _con[_con.size() - 1]); _con.pop_back(); AdjustDown(_con.size(), 0); //将第0个元素进行一次向下调整 } //访问队头元素(堆顶元素) T& top() { return _con[0]; } const T& top() const { return _con[0]; } //获取队列中有效元素个数 size_t size() const { return _con.size(); } //判断队列是否为空 bool empty() const { return _con.empty(); } private: Container _con; //底层容器 Compare _comp; //比较方式 }; }
C++STL— priority_queue的使用与模拟实现内容到此介绍结束了,感谢您的阅读!!!
如果内容对你有帮助的话,记得给我点个赞——做个手有余香的人。感谢大家的支持!!!