在这里插入图片描述

系列文章目录

作者：i阿极

作者简介：Python领域新星作者、多项比赛获奖者：博主个人首页

😊😊😊如果觉得文章不错或能帮助到你学习，可以点赞👍收藏📁评论📒+关注哦！👍👍👍

📜📜📜如果有小伙伴需要数据集和学习交流，文章下方有交流学习区！一起学习进步！💪

大家好，我i阿极。喜欢本专栏的小伙伴，请多多支持

专栏案例：机器学习案例
机器学习(一)：线性回归之最小二乘法
机器学习(二)：线性回归之梯度下降法
机器学习(三)：基于线性回归对波士顿房价预测
机器学习(四)：基于KNN算法对鸢尾花类别进行分类预测
机器学习(五)：基于KNN模型对高炉发电量进行回归预测分析
机器学习(六)：基于高斯贝叶斯对面部皮肤进行预测分析
机器学习(七)：基于多项式贝叶斯对蘑菇毒性分类预测分析
机器学习(八)：基于PCA对人脸识别数据降维并建立KNN模型检验
机器学习(十四)：基于逻辑回归对超市销售活动预测分析
机器学习(十五)：基于神经网络对用户评论情感分析预测
机器学习(十六)：基于Kmeans聚类算法对银行客户进行分类
机器学习(十七)：基于支持向量机（SVM）进行人脸识别预测
机器学习(十八)：基于逻辑回归对优惠券使用情况预测分析
机器学习(十九）：基于逻辑回归对某银行客户违约预测分析
机器学习(二十)：LightGBM算法原理（附案例实战）
机器学习(二十一)：基于朴素贝叶斯对花瓣花萼的宽度和长度分类预测
机器学习(二十二)：基于逻辑回归（Logistic Regression）对股票客户流失预测分析

文章目录

系列文章目录
1、Apriori算法模型原理
2、实验环境
3、Apriori算法模型案例理解
4、Apriori算法模型综合案例
- 4.1案例背景
- 4.2数据读取与预处理
- 4.3 apyori库实现关联
- 4.4mlxtend库实现关联
总结

1、Apriori算法模型原理

Apriori算法是一种经典的关联规则挖掘算法，用于发现数据集中频繁出现的项集和关联规则。该算法基于一种称为"先验原理"的观念，即如果一个项集是频繁的，那么它的所有子集也必须是频繁的。通过利用这个原理，Apriori算法逐步构建频繁项集，并生成关联规则。

下面是Apriori算法的详细步骤：

确定最小支持度阈值：用户需要指定一个最小支持度阈值，用于筛选出频繁项集。支持度定义为某个项集在数据集中出现的频率。
生成候选项集：初始时，算法将每个项作为单独的候选项集。然后，通过扫描数据集，计算每个候选项集的支持度，并筛选出满足最小支持度阈值的频繁一项集。
组合生成更高阶的候选项集：对于频繁一项集，算法使用连接操作生成候选项集。连接操作是指将两个频繁项集合并为一个更高阶的候选项集。具体来说，对于每个频繁k-1项集，算法将其按字典序排序，并两两组合生成候选k项集。
剪枝步骤：在生成候选项集后，需要进行剪枝操作以减少计算量。剪枝操作通过检查候选项集的所有(k-1)项子集是否都是频繁项集来实现。如果存在某个(k-1)项子集不是频繁项集，则将候选项集删除。
计算候选项集的支持度：对剪枝后的候选项集，再次扫描数据集，计算它们的支持度，并筛选出满足最小支持度阈值的频繁项集。
重复步骤3至步骤5：重复进行组合生成候选项集、剪枝和计算支持度的步骤，直到无法生成更高阶的候选项集为止。
生成关联规则：在获得频繁项集后，可以生成关联规则。对于每个频繁项集，算法产生其所有非空子集作为候选规则。然后，通过计算置信度筛选出满足最小置信度阈值的关联规则。

2、实验环境

Python 3.9

Jupyter Notebook

Anaconda

3、Apriori算法模型案例理解

当我们使用Apriori算法来分析市场购物篮数据时，假设有以下几个项集和关联规则：

项集（物品组合）：

{牛奶}
{面包}
{啤酒}
{牛奶, 面包}
{牛奶, 啤酒}
{面包, 啤酒}
{牛奶, 面包, 啤酒}

关联规则：

{牛奶} => {面包}
{面包} => {牛奶}
{啤酒} => {牛奶}
{牛奶, 面包} => {啤酒}
{面包, 啤酒} => {牛奶}
{牛奶, 啤酒} => {面包}

假设我们设置最小支持度阈值为3，即项集的出现次数至少为3次才被认为是频繁项集。

首先，我们生成频繁一项集。根据市场购物篮数据统计，我们得到以下频繁一项集：

{牛奶} (出现次数：4)
{面包} (出现次数：4)
{啤酒} (出现次数：3)

接下来，我们通过组合生成更高阶的候选项集。由于只有3个频繁一项集，我们可以直接生成候选二项集：

{牛奶, 面包}
{牛奶, 啤酒}
{面包, 啤酒}

然后，进行剪枝操作。根据先验原理，我们检查候选二项集的所有一项子集是否都是频繁一项集。由于{牛奶, 面包}、{牛奶, 啤酒}和{面包, 啤酒}的所有一项子集都是频繁一项集，它们都被保留。

接着，计算候选二项集的支持度。我们再次扫描市场购物篮数据，计算候选二项集的出现次数：

{牛奶, 面包} (出现次数：3)
{牛奶, 啤酒} (出现次数：2)
{面包, 啤酒} (出现次数：3)

根据最小支持度阈值为3，我们筛选出频繁二项集：

{牛奶, 面包} (出现次数：3)
{面包, 啤酒} (出现次数：3)

现在，我们已经得到了频繁二项集。我们可以继续进行组合生成候选三项集，然后进行剪枝和计算支持度的操作，直到无法生成更高阶的候选项集为止。

最后，通过频繁项集可以生成关联规则。关联规则是由频繁项集中的子集生成的。我们可以使用支持度和置信度来评估关联规则的强度和可靠性。在上述的案例中，我们已经给出了几个关联规则示例。

通过以上的案例，我们可以看到Apriori算法是通过迭代的方式从频繁一项集开始，不断生成候选项集并进行剪枝和计算支持度的操作，最终得到频繁项集和关联规则。这样，我们就可以发现市场购物篮中的常见组合和关联关系，为市场营销和推荐系统等提供支持和指导。

4、Apriori算法模型综合案例

4.1案例背景

在中医领域往往强调相生相克的辩证关系，即我们的五脏六腑不仅仅是一个个独立的个体，而是一个个具有相互联系的存在，有的时候某一个脏器出了问题，可能不仅仅是由于该脏器本身导致的，而是其关联的脏器一起导致的现象，举例来说，有的人经常感觉到心悸，按理说，这个是心脏的问题，但是在中医的角度，很可能是和心脏相关的脏器：肝出现了问题导致了心悸这一病症。

在中医理论中，常把五脏和中国的五行学说结合到一起，配合五行相生相克的关联规则去分析五脏之间的关联规则，如下表所示：
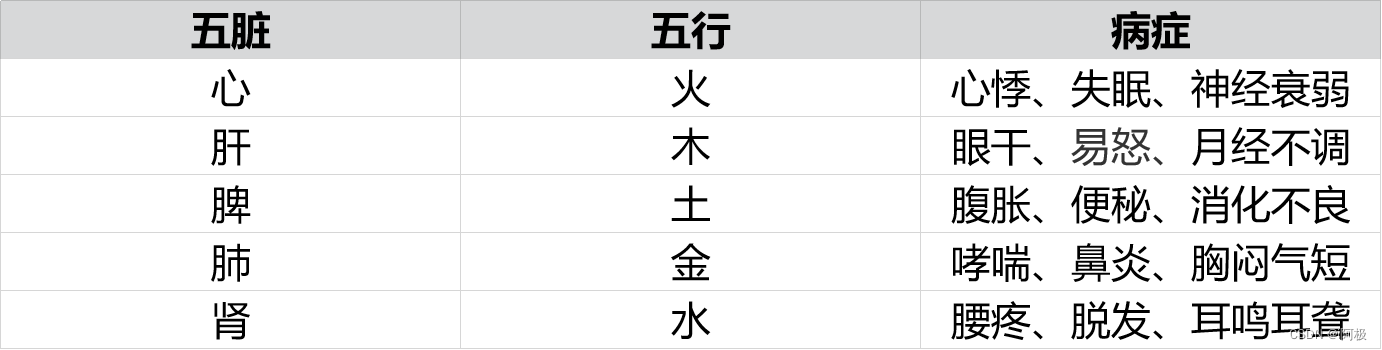
在这里插入图片描述

4.2数据读取与预处理

导入数据

import pandas as pd
df = pd.read_excel('中医辨证.xlsx')
df.head()

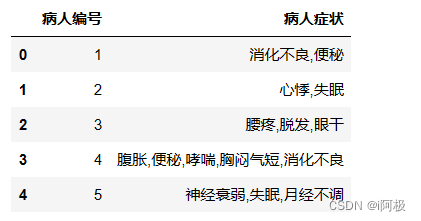
在这里插入图片描述

将”病人症状“列的值转为列表存储

df['病人症状'].tolist()

在这里插入图片描述

转换为双重列表结构

symptoms = []
for i in df['病人症状'].tolist():
    symptoms.append(i.split(','))
print(symptoms)

在这里插入图片描述

4.3 apyori库实现关联

调用apyori库中的apriori()函数来进行关联关系分析

from apyori import apriori
rules = apriori(symptoms, min_support=0.1, min_confidence=0.7)
results = list(rules)

for i in results:  # 遍历results中的每一个频繁项集
    for j in i.ordered_statistics:  # 获取频繁项集中的关联规则
        X = j.items_base  # 关联规则的前件
        Y = j.items_add  # 关联规则的后件
        x = ', '.join([item for item in X])  # 连接前件中的元素
        y = ', '.join([item for item in Y])  # 连接后件中的元素
        if x != '':  # 防止出现关联规则前件为空的情况
            print(x + ' → ' + y)  # 通过字符串拼接的方式更好呈现结果

在这里插入图片描述

4.4mlxtend库实现关联

from mlxtend.preprocessing import TransactionEncoder
TE = TransactionEncoder()  # 构造转换模型
data = TE.fit_transform(symptoms)  # 将原始数据转化为bool值
data

在这里插入图片描述

用DataFrame存储bool数据

import pandas as pd
df = pd.DataFrame(data, columns=TE.columns_) 
df.head()

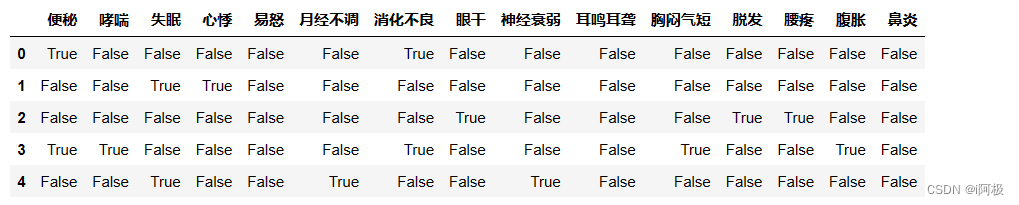
在这里插入图片描述

from mlxtend.frequent_patterns import apriori
items = apriori(df, min_support=0.1, use_colnames=True)
items.head()

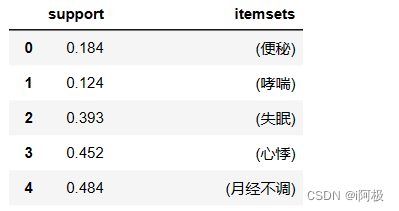
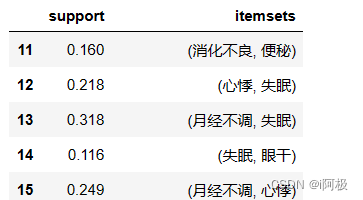
在这里插入图片描述

items[items['itemsets'].apply(lambda x: len(x)) >= 2]

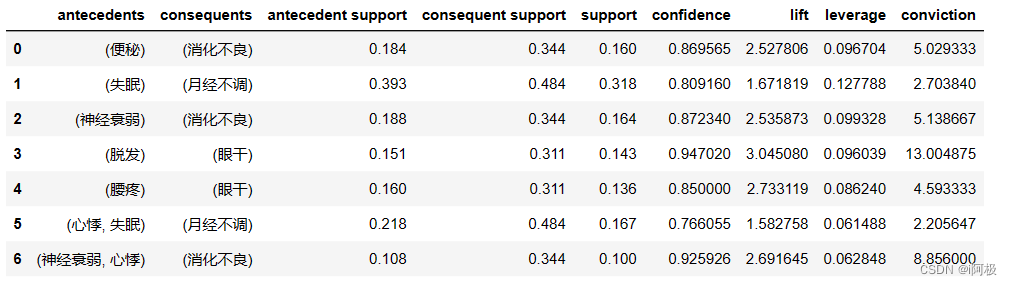
在这里插入图片描述

from mlxtend.frequent_patterns import association_rules
rules = association_rules(items, min_threshold=0.7)
rules

在这里插入图片描述

for i, j in rules.iterrows():  # 遍历DataFrame二维表格的每一行
    X = j['antecedents']  # 关联规则的前件
    Y = j['consequents']  # 关联规则的后件
    x = ', '.join([item for item in X])  # 连接前件中的元素
    y = ', '.join([item for item in Y])  # 连接后件中的元素
    print(x + ' → ' + y)  # 通过字符串拼接打印关联规则

在这里插入图片描述

总结

Apriori算法的优点是简单易懂，容易实现，而且可以发现数据集中的频繁项集和关联规则。然而，对于大规模数据集，Apriori算法需要生成大量的候选项集，计算支持度的开销较大，效率较低。为了解决这个问题，后续还提出了改进的Apriori算法，如FP-Growth算法，利用了数据集的频繁模式树结构，加速了频繁项集的挖掘过程。