给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格(即,(0, 0))到 右下角 单元格(即,(n - 1, n - 1))的路径,该路径同时满足下述要求:
路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通(即,相邻两单元之间彼此不同且共享一条边或者一个角)。
畅通路径的长度 是该路径途经的单元格总数。
示例 1:
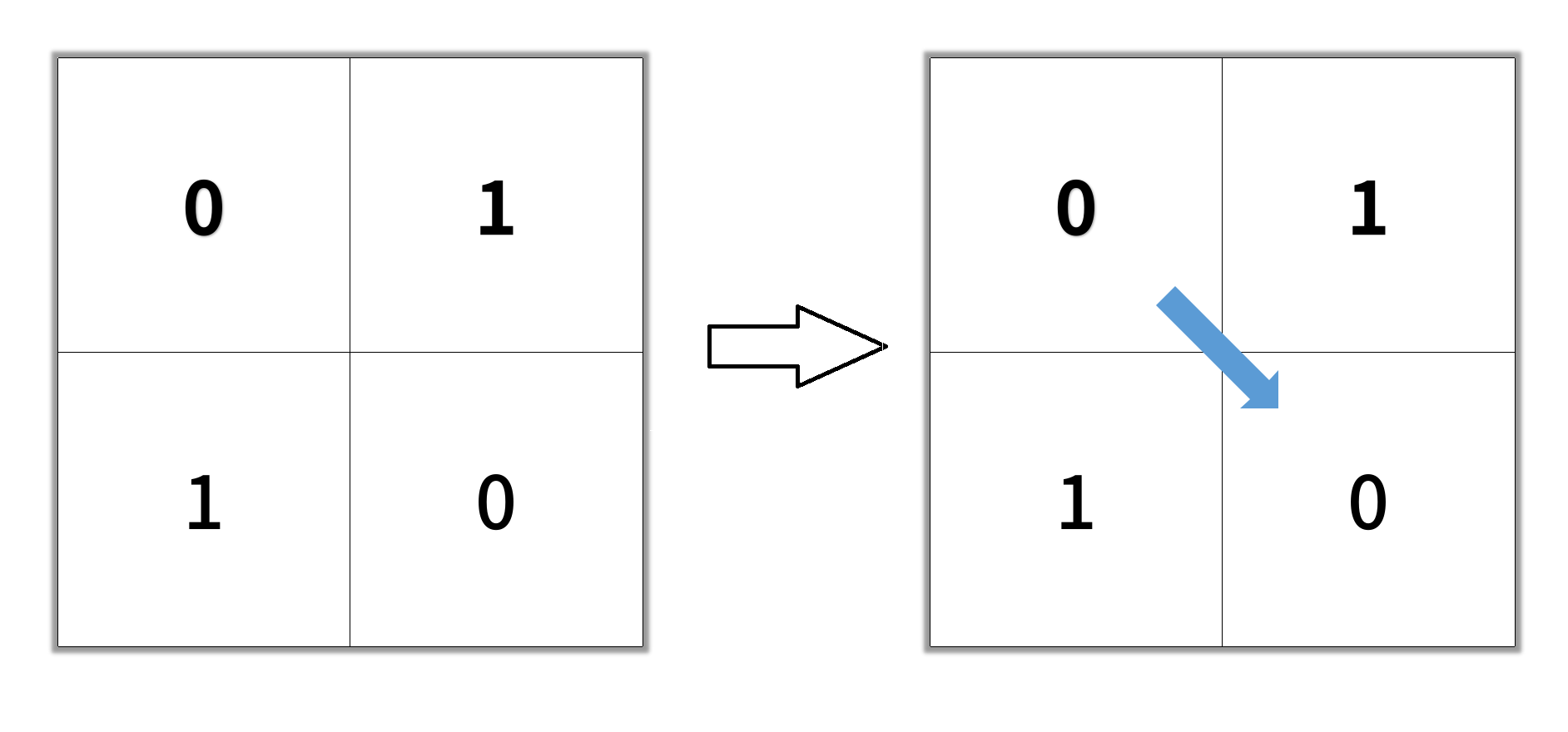
输入:grid = [[0,1],[1,0]]
输出:2
示例 2:
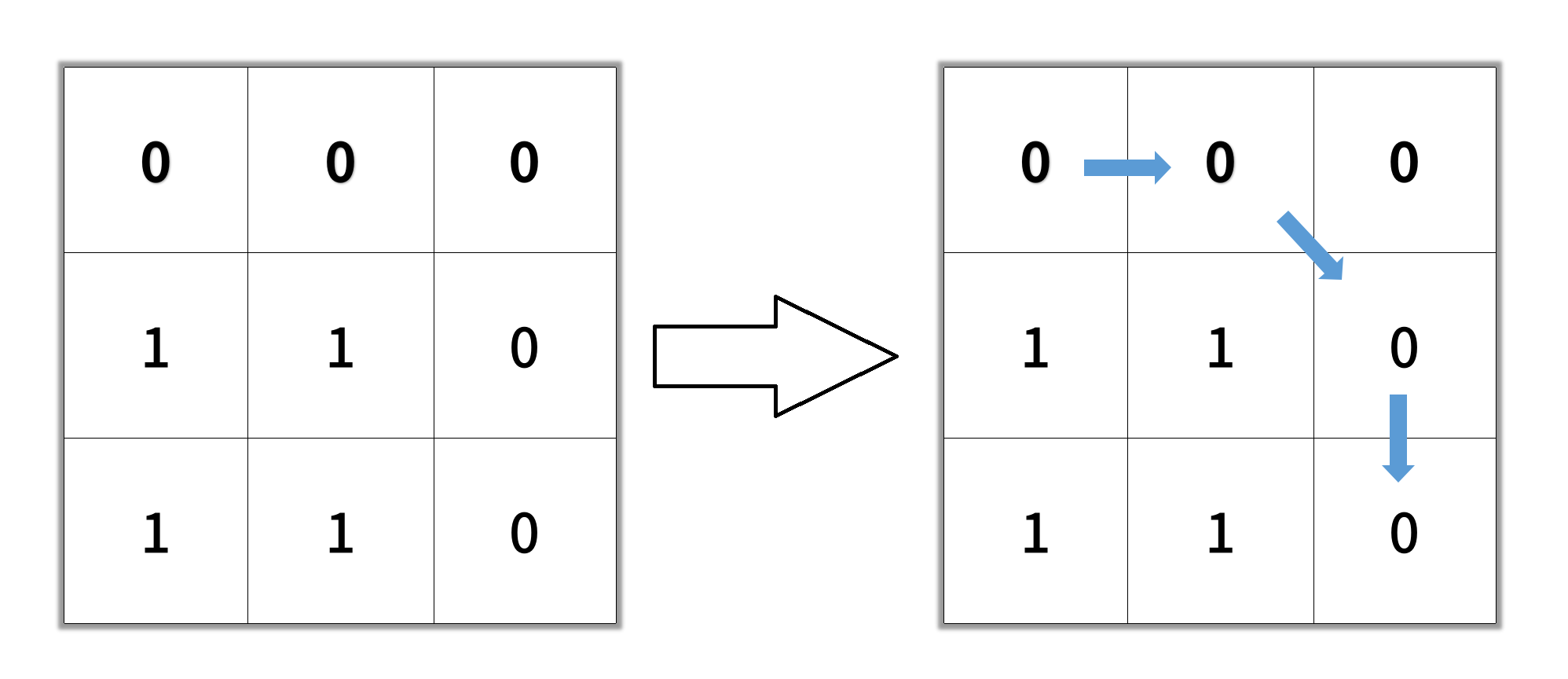
输入:grid = [[0,0,0],[1,1,0],[1,1,0]]
输出:4
示例 3:
输入:grid = [[1,0,0],[1,1,0],[1,1,0]]
输出:-1
提示:
n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] 为 0 或 1
可以说是广搜剪枝的超级典型的题目了,看题目要求是地图上寻找路径,下意识反应过来是搜索,再看题目要求,寻找所有路径中最短的,找一个用深搜找全部用广搜,所以直接套用八方向广搜的模板,题目的时间要求给的很宽松,不剪枝也能过。
class Solution {
public:
int dir[8][2] = {0,1,0,-1,1,0,-1,0,1,1,1,-1,-1,1,-1,-1};
bool flag[105][105];
int n, ans = 99999;
int shortestPathBinaryMatrix(vector<vector<int> >& grid){
n = grid[0].size();
int sx, sy, ex, ey;
sx = 0;
sy = 0;
ex = n - 1;
ey = n - 1;
if(grid[sx][sy]==1)
return -1;
queue<pair<pair<int, int>, int> > q;
q.push(make_pair(make_pair(sx, sy), 1));
while(!q.empty()){
pair<pair<int, int>, int> temp = q.front();
q.pop();
int nx = temp.first.first;
int ny = temp.first.second;
int cost = temp.second;
if(nx==ex&&ny==ey){
ans = min(ans, cost);
}
for(int i=0; i<8; i++){
int tx = nx + dir[i][0];
int ty = ny + dir[i][1];
if(tx<0||ty<0||tx>=n||ty>=n)
continue;
if(flag[tx][ty]==true)
continue;
if(grid[tx][ty]==1)
continue;
flag[tx][ty] = 1;
q.push(make_pair(make_pair(tx, ty), cost+1));
}
}
if(ans!=99999)
return ans;
else
return -1;
}
};
在此基础上在加入剪枝的内容,也就是在遍历过程中,如果当前节点的路径长度已经超过了目前最优值,那么就没有沿这个节点继续搜索下去的必要,对这个节点就不需要继续处理。剪枝后时间复杂度能够有提升。
class Solution {
public:
int dir[8][2] = {0,1,0,-1,1,0,-1,0,1,1,1,-1,-1,1,-1,-1};
bool flag[105][105];
int n, ans = 99999;
int shortestPathBinaryMatrix(vector<vector<int> >& grid){
n = grid[0].size();
int sx, sy, ex, ey;
sx = 0;
sy = 0;
ex = n - 1;
ey = n - 1;
if(grid[sx][sy]==1)
return -1;
queue<pair<pair<int, int>, int> > q;
q.push(make_pair(make_pair(sx, sy), 1));
while(!q.empty()){
pair<pair<int, int>, int> temp = q.front();
q.pop();
int nx = temp.first.first;
int ny = temp.first.second;
int cost = temp.second;
if(cost>ans)
continue;
if(nx==ex&&ny==ey){
ans = min(ans, cost);
}
for(int i=0; i<8; i++){
int tx = nx + dir[i][0];
int ty = ny + dir[i][1];
if(tx<0||ty<0||tx>=n||ty>=n)
continue;
if(flag[tx][ty]==true)
continue;
if(grid[tx][ty]==1)
continue;
flag[tx][ty] = 1;
q.push(make_pair(make_pair(tx, ty), cost+1));
}
}
if(ans!=99999)
return ans;
else
return -1;
}
};
关于空间复杂度,也可以优化pair的写法,用单独一个变量来存储到当前节点的距离,这样就不需要在pair中额外添加存储量,按道理空间复杂度还可以提升。