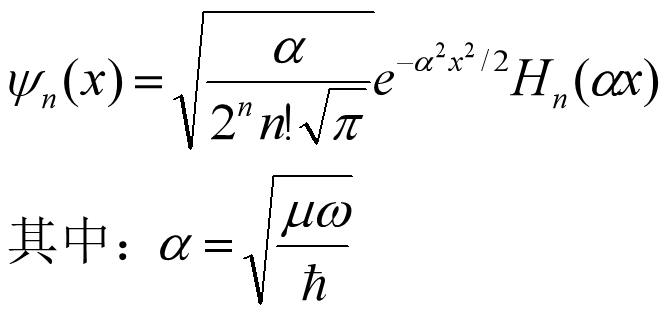• 任何体系在平衡位置附近的小振动，例如 分子振动、晶格振动、原子核表面振动以及辐射场的振动等往往都可以分解成 若干彼此独立的一维简谐振动
• 简谐振动往往还作为复杂运动的初步近似 见理论力学专题（小振动）
  • 双原子分子，两原子间的势V是二者相对距离x的函数
    • 在 x = a 处，V 有一极小值V_0
    • 在 x = a 附近势可以展开成泰勒级数

 

 

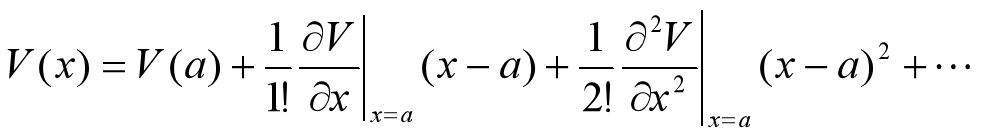
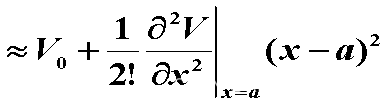
• 取新坐标原点为(a, V0)，则势可表示为标准谐振子势的形式：

线性谐振子

线性谐振子的 Hamilton量:

 

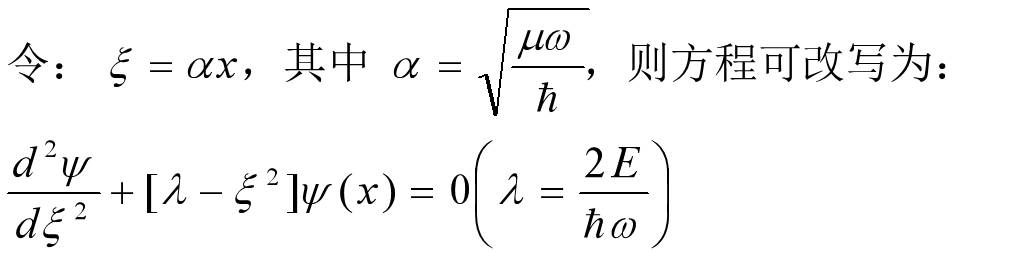
求解

渐近解(λ<< ξ2)

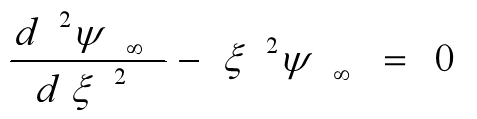
解析解

•  其中 H(ξ) 必须满足波函数的单值、有限、连续的标准条件。即：
  • 当ξ有限时，H(ξ)有限
  • 当ξ→∞时，H(ξ)的行为要保证ψ(ξ)→ 0

级数

令:

 

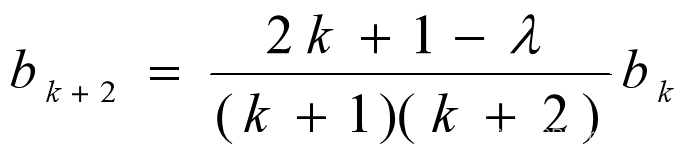
• b0   决定所有角标k为偶数的系数；  
• b1   决定所有角标k为奇数的系数。

有限性条件

• H(ξ)是一个幂级数，故应考虑他的收敛性。考虑一些特殊点， 即势场有跳跃的地方以及x=0, x → ±∞或ξ=0, ξ→±∞

•  当ξ→±∞时， H(ξ)的渐近 行为与exp[ξ^2]相同

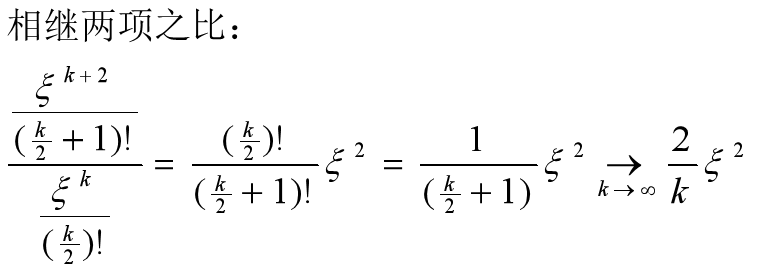
•  所以总波函数有如下发散行为：

•  为了满足波函数有限性要求，幂级数 H(ξ) 必须从某一项截断变成一个多项式。

• 基于波函数在无穷远处的有限性条件导致了能量必须取分立值。

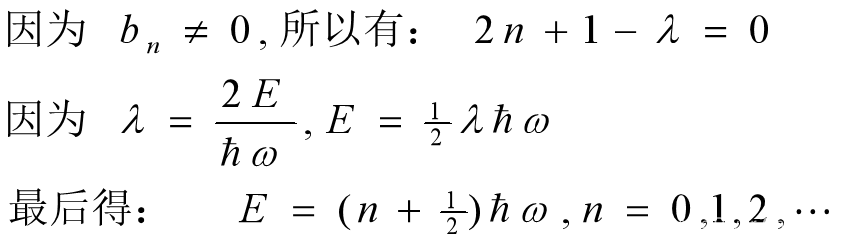
厄密多项式

 

• 厄密多项式和谐振子波函数的递推关系