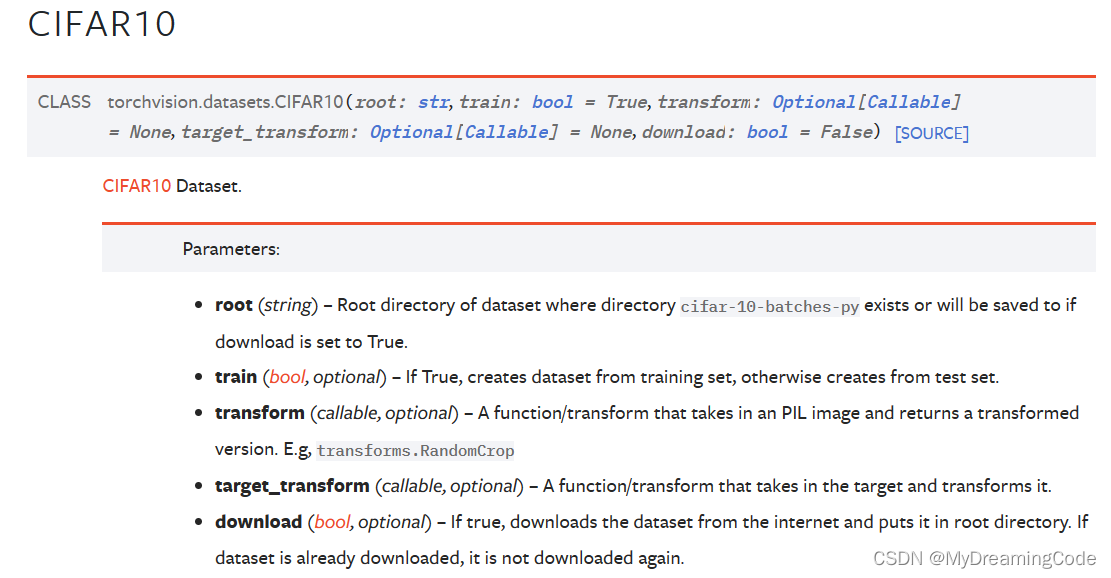
1. 以Torchvision中的CIFAR10为例

dataset.py

Ps：如果是从其他地方下载的gz文件，直接建立一个dataset文件夹然后将gz文件放进去，再运行。 

import torchvision

train_set = torchvision.datasets.CIFAR10(root="./dataset", train=True, download=True)
test_set = torchvision.datasets.CIFAR10(root='./dataset', train=False, download=True)
img, target = test_set[0]
print(img, target)
print(test_set.classes[target])
img.show()

result:

<PIL.Image.Image image mode=RGB size=32x32 at 0x1F9FA5D3E50> 3
cat

2. 加入transforms

dataset.py

import torchvision
from torch.utils.tensorboard import SummaryWriter

dataset_transform = torchvision.transforms.Compose([
    torchvision.transforms.ToTensor()
])
train_set = torchvision.datasets.CIFAR10(root="./dataset", train=True, transform=dataset_transform, download=True)
test_set = torchvision.datasets.CIFAR10(root='./dataset', train=False, transform=dataset_transform, download=True)
print(test_set[0])
writer = SummaryWriter('cifa10')
for i in range(10):
    img, target = test_set[i]
    writer.add_image('test_set', img, i)
writer.close()

result:

(tensor([[[0.6196, 0.6235, 0.6471,  ..., 0.5373, 0.4941, 0.4549],
         [0.5961, 0.5922, 0.6235,  ..., 0.5333, 0.4902, 0.4667],
         [0.5922, 0.5922, 0.6196,  ..., 0.5451, 0.5098, 0.4706],
         ...,
         [0.2667, 0.1647, 0.1216,  ..., 0.1490, 0.0510, 0.1569],
         [0.2392, 0.1922, 0.1373,  ..., 0.1020, 0.1137, 0.0784],
         [0.2118, 0.2196, 0.1765,  ..., 0.0941, 0.1333, 0.0824]],

        [[0.4392, 0.4353, 0.4549,  ..., 0.3725, 0.3569, 0.3333],
         [0.4392, 0.4314, 0.4471,  ..., 0.3725, 0.3569, 0.3451],
         [0.4314, 0.4275, 0.4353,  ..., 0.3843, 0.3725, 0.3490],
         ...,
         [0.4863, 0.3922, 0.3451,  ..., 0.3804, 0.2510, 0.3333],
         [0.4549, 0.4000, 0.3333,  ..., 0.3216, 0.3216, 0.2510],
         [0.4196, 0.4118, 0.3490,  ..., 0.3020, 0.3294, 0.2627]],

        [[0.1922, 0.1843, 0.2000,  ..., 0.1412, 0.1412, 0.1294],
         [0.2000, 0.1569, 0.1765,  ..., 0.1216, 0.1255, 0.1333],
         [0.1843, 0.1294, 0.1412,  ..., 0.1333, 0.1333, 0.1294],
         ...,
         [0.6941, 0.5804, 0.5373,  ..., 0.5725, 0.4235, 0.4980],
         [0.6588, 0.5804, 0.5176,  ..., 0.5098, 0.4941, 0.4196],
         [0.6275, 0.5843, 0.5176,  ..., 0.4863, 0.5059, 0.4314]]]), 3)

Process finished with exit code 0