1. 定义
给定欧氏空间中的两点集
A
=
{
a
1
,
a
2
,
.
.
.
}
\rm A=\left \{a_1, a_2,... \right\}
A={a1,a2,...} 和
B
=
{
b
1
,
b
2
,
.
.
.
}
\rm B=\left \{b_1, b_2,... \right\}
B={b1,b2,...} ,
H
a
u
s
d
o
r
f
f
{\rm Hausdorff}
Hausdorff 距离就是用来衡量这两个集合间的距离,定义其公式为:
H
(
A
,
B
)
=
m
a
x
[
h
(
A
,
B
)
,
h
(
B
,
A
)
]
{\rm H\left (A,B\right)}={\rm max}\left [\:h(A,B), h(B,A)\: \right]
H(A,B)=max[h(A,B),h(B,A)]
其中,
h
(
A
,
B
)
=
m
a
x
a
∈
A
m
i
n
b
∈
B
∥
a
−
b
∥
\rm h\left(A,B\right)=\underset{a\in A}{max} \: \underset{b\in B}{min} \left \|a-b \right \|
h(A,B)=a∈Amaxb∈Bmin∥a−b∥
h
(
B
,
A
)
=
m
a
x
b
∈
B
m
i
n
a
∈
A
∥
b
−
a
∥
\rm h\left(B,A\right)=\rm\underset{b\in B}{max} \: \underset{a\in A}{min} \left \|b-a \right \|
h(B,A)=b∈Bmaxa∈Amin∥b−a∥
H
(
A
,
B
)
\rm H \left(A,B\right)
H(A,B) 称为双向
H
a
u
s
d
o
r
f
f
{\rm Hausdorff}
Hausdorff距离,
h
(
A
,
B
)
\rm h \left(A,B\right)
h(A,B)称为从集合
A
\rm A
A到集合
B
\rm B
B的单向
H
a
u
s
d
o
r
f
f
{\rm Hausdorff}
Hausdorff距离,同理,
h
(
B
,
A
)
{\rm h \left(B,A\right)}
h(B,A)称为从集合
B
{\rm B}
B到集合
A
{\rm A}
A的单向
H
a
u
s
d
o
r
f
f
{\rm Hausdorff}
Hausdorff距离。
2. 通过例子理解该定义
详见该篇blog中的例子:
https://blog.csdn.net/maizousidemao/article/details/105030333?ydreferer=aHR0cHM6Ly9ibG9nLnNjaWVuY2VuZXQuY24v
理解
H
a
u
s
d
o
r
f
f
{\rm Hausdorff}
Hausdorff衡量距离的计算逻辑后,在使用时,可以直接用Python包👇🏻
(看完例子还不懂怎么计算的,看下面的解释)
3. 用Python计算 H a u s d o r f f {\rm Hausdorff} Hausdorff距离
- 导入第三方包👇🏻
from scipy.spatial.distance import directed_hausdorff
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics.pairwise import euclidean_distances
- 官方给出的算例,给定两个集合 u \rm u u和 v \rm v v👇🏻
u = np.array([(1.0, 0.0),
(0.0, 1.0),
(-1.0, 0.0),
(0.0, -1.0)])
v = np.array([(2.0, 0.0),
(0.0, 2.0),
(-2.0, 0.0),
(0.0, -4.0)])
- 调用函数
directed_hausdorff(u,v),求得单向 H a u s d o r f f {\rm Hausdorff} Hausdorff距离,并计算双向 H a u s d o r f f {\rm Hausdorff} Hausdorff距离👇🏻
directed_hausdorff(u,v) # 计算u到v的单向Hausdorff距离
--->输出为:(2.23606797749979, 3, 0)
directed_hausdorff(v,u) # 计算v到u的单向Hausdorff距离
--->输出为:(3.0, 3, 3)
hausdorff_distance = max(directed_hausdorff(u,v)[0],directed_hausdorff(v,u)[0]) # 计算u与v之间的双向Hausdorff距离
print(hausdorff_distance)
--->输出为:(3.0)
4. 结果解释与理解
(1) 关于directed_hausdorff(u,v)输出值的解释。
- \;\;\; 结果 ( 2.236 , 3 , 0 ) (2.236, 3, 0) (2.236,3,0)中,第1个值指 u \rm u u到 v \rm v v的单向 H a u s d o r f f \rm Hausdorff Hausdorff距离为2.236,第2和3个值指的是,产生距离为2.236的两个数据点分别在集合 u \rm u u和集合 v \rm v v中的位置,如 ( 3 , 0 ) (3,0) (3,0)指的是 u 3 = [ 0 , − 1 ] \rm u_3=[0,-1] u3=[0,−1]和 v 0 = [ 2 , 0 ] \rm v_0=[2,0] v0=[2,0]。
- \;\;\; 结果 ( 3.0 , 3 , 3 ) (3.0, 3, 3) (3.0,3,3)同理,第1个值指 v \rm v v到 u \rm u u的单向 H a u s d o r f f \rm Hausdorff Hausdorff距离为3,第2和3个值指的是,产生距离为3的两个数据点分别在集合 u \rm u u和集合 v \rm v v中的位置,如 ( 3 , 0 ) (3,0) (3,0)指的是 v 3 = [ 0 , − 4 ] \rm v_3=[0,-4] v3=[0,−4]和 u 3 = [ 0 , − 1 ] \rm u_3=[0,-1] u3=[0,−1]。
(2)手算该过程,直观地解释。
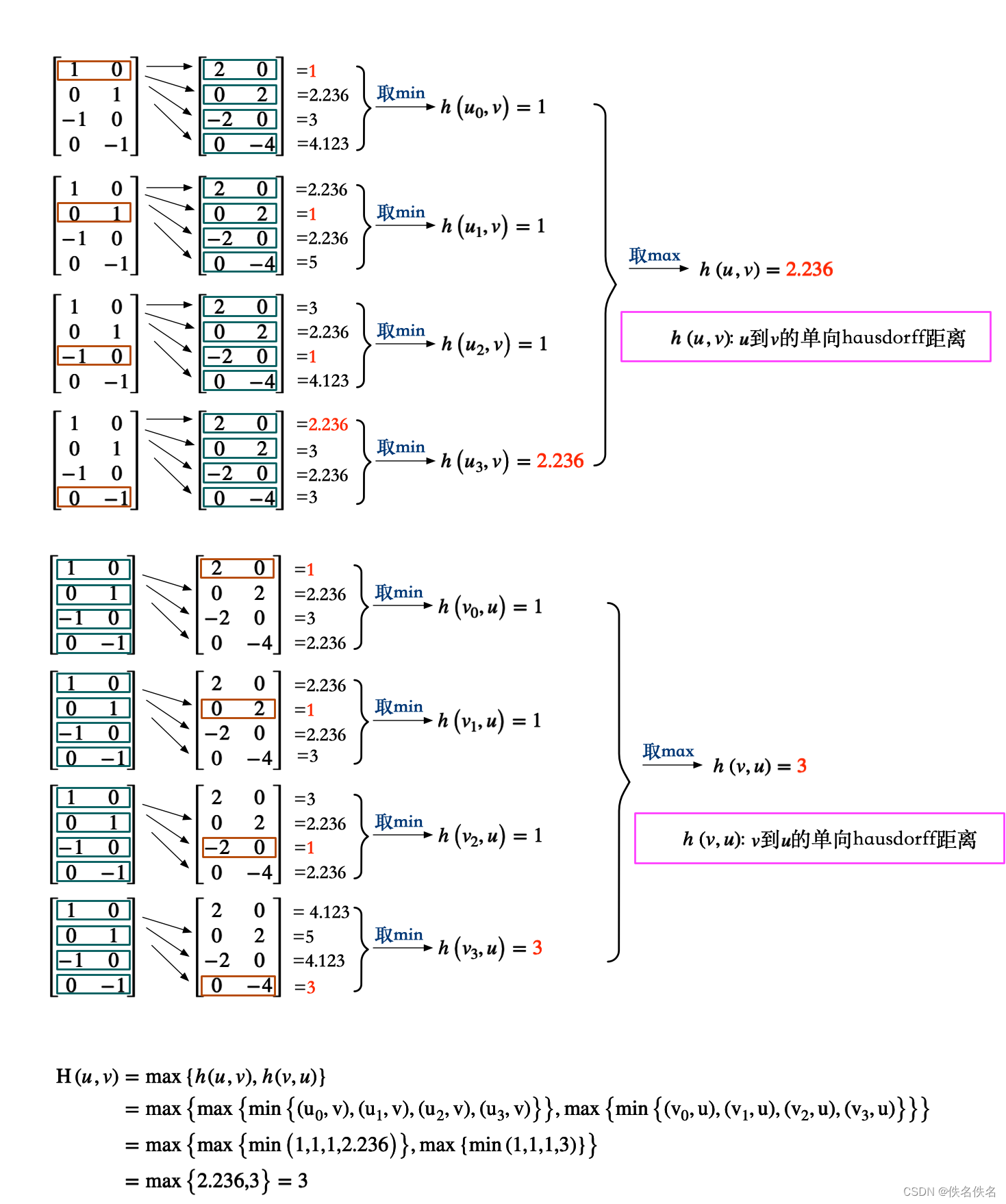
(3) 辅助理解。计算
u
\rm u
u与
v
\rm v
v、
v
\rm v
v和
u
\rm u
u之间的欧氏距离,更容易了解该过程。下述结果👇🏻一一对应上图中的手算结果。
euclidean_distances(u,v) #
---->输出为:
array([[1. , 2.23606798, 3. , 4.12310563],
[2.23606798, 1. , 2.23606798, 5. ],
[3. , 2.23606798, 1. , 4.12310563],
[2.23606798, 3. , 2.23606798, 3. ]])
euclidean_distances(v,u)
--->输出为:
array([[1. , 2.23606798, 3. , 2.23606798],
[2.23606798, 1. , 2.23606798, 3. ],
[3. , 2.23606798, 1. , 2.23606798],
[4.12310563, 5. , 4.12310563, 3. ]])