目录
- 摘要
- 1. 引言
- 2. DeepfilterNet
- 2.1. 信号模型
- 2.2. Deep Filtering
- 2.3. 框架概述
- 2.4. DNN模型
- 2.5. 数据处理
- 2.6. 损失函数
- 3. 实验
- 3.1. 训练步骤
- 3.2. 结果
- 4. 结论
- 5. 参考文献
论文题目:DeepFilterNet: A Low Complexity Speech Enhancement Framework for Full-Band Audio based on Deep Filtering
题目译文:DeepFilterNet:基于深度滤波器的全频带音频低复杂度语音增强框架
论文地址:https://arxiv.org/abs/2110.05588
论文代码:https://github.com/Rikorose/DeepFilterNet
引用:Schröter H, Rosenkranz T, Maier A. DeepFilterNet: A Low Complexity Speech Enhancement Framework for Full-Band Audio based on Deep Filtering[J]. arXiv preprint arXiv:2110.05588, 2021.
摘要
复数处理将基于深度学习的语音增强和信号提取提升到一个新的水平。通常,将时频 (TF) 掩膜应用于噪声频谱,而复数掩模(CM)通常比实值掩模更受青睐,因为它们能够修改相位。最近的工作提出用一个复数滤波器代替掩码的逐点乘法。这允许利用每个频带内的局部相关性,将以前和将来的时间步长的信息合并到一起。
在这项工作中,我们提出了DeepFilterNet,一个利用深度滤波器的两阶段语音增强框架。首先,我们使用模拟人类频率感知的 ERB-scale gain来增强频谱包络。第二阶段采用Deep filtering 增强语音的周期性成分。除了利用语音的感知特性之外,我们还通过深度分离卷积、分组线性网络、分组循环网络 来强制网络稀疏性,以设计一个低复杂度的架构。
我们进一步表明,我们的两阶段深度滤波方法在各种频率分辨率和延迟上都优于复数掩码,并且与其他最先进的模型相比,表现出令人信服的性能。
关键词:deep filtering、语音增强
1. 引言
单声道语音增强是许多系统的重要组成部分,如自动语音识别、视频会议系统以及辅助听设备。大多数最先进的方法都是在短时傅里叶变换(STFT)表示中工作,并使用深度神经网络估计TF mask,其中许多是实值掩模[1,2,3]或复数掩模[4,5,6,7]。为了提高网络训练的稳定性,估计的掩码通常是定义良好的,并受一个上界的限制(0~1)。然而,通常情况下,这两种方法都会降低频率分辨率,以消除语音谐波之间的噪声。上述方法在至少20 ms的窗口上工作,导致最低频率为50 Hz。
在本文中,我们提出了一个基于深度滤波器(DF)的开源语音增强框架[8,9]。我们使用实值增益和深度滤波器组合,而不是在每个TF-bin上应用复数掩模。第一阶段,因为噪声和语音通常有一个平滑的频谱包络。我们使用一个等效的矩形带宽(Equivalent Rectangular Bandwidth,ERB)滤波器组将输入和输出size降低到只有32个频带,并设计一个计算量小的编码器/解码器网络。由于最终得到的100 Hz到250 Hz的最小带宽(取决于FFT size)通常不足以增强周期分量。因此在第二阶段,我们使用深度滤波器网络估计频率区间的系数,直到频率上限
f
D
F
f_{DF}
fDF。将得到的线性复数滤波器应用于它们相应的频率区间。 DF 增强仅适用于较低频率,因为周期性语音分量在较低频率中包含大部分能量。
深度滤波器首先由Mack et al.[8]和Schr oter et al.[9]提出。由于滤波器应用于多个T-F bin,DF能够恢复信号退化,如缺口滤波器(notch-filters)或时间帧归零(time-frame zeroing)。Schroter等人[9]将这种方法作为复杂线性编码(Complex Linear Coding,CLC)引入到低延迟助听器的应用中。CLC的动机是它能够模拟语音的准静态特性。也就是说,即使在500 Hz的频率带宽下,CLC也能够在一个频带内降低噪声,同时保留语音成分。当一个频率库中有多个语音谐波或用于过滤周期性噪声时,这特别有用。最近的工作表明,[7]使用深度滤波器在深度噪声抑制挑战[10]中表现良好。然而,与他们之前使用复杂比率掩码(CRM)的工作[11]相比,他们的改进主要是通过网络架构的改变,如复数 LSTM或卷积。
在这项工作中,我们证明了从4 ms到30 ms的多种FFT大小的CRMs深度滤波器的优越性能。我们进一步表明,即使对于低延迟要求,例如5毫秒,从而产生250 Hz的频率分辨率(
Δ
f
=
f
s
N
=
1
t
\Delta{f}=\frac{f_s}{N}=\frac{1}{t}
Δf=Nfs=t1,其中采样频率为
f
s
f_s
fs,采样时间间隔为t,采样点数为N),DF仍然可以增强周期性语音成分。
2. DeepfilterNet
2.1. 信号模型
设
x
(
t
)
x(t)
x(t)为在嘈杂房间中录制的混合信号。
x
(
t
)
=
s
(
t
)
∗
h
(
t
)
+
z
(
t
)
x(t)=s(t)*h(t)+z(t)
x(t)=s(t)∗h(t)+z(t)
式中,
s
(
t
)
s(t)
s(t)为纯净语音信号,
h
(
t
)
h(t)
h(t)为扬声器对麦克风的室内脉冲响应,
z
(
t
)
z(t)
z(t)为已包含混响环境的加性噪声信号。通常,降噪是在频域进行的:
X
(
k
,
f
)
=
S
(
k
,
f
)
⋅
H
(
k
,
f
)
+
Z
(
k
,
f
)
X(k,f)=S(k,f)·H(k,f)+Z(k,f)
X(k,f)=S(k,f)⋅H(k,f)+Z(k,f)
其中X(k,f)是时域信号
x
(
t
)
x(t)
x(t)的STFT结果,
k
k
k和
f
f
f分别是时间和频率bin 索引。
2.2. Deep Filtering
Deep Filtering被定义为 TF域的 复数滤波器:
Y
(
k
,
f
)
=
∑
i
=
0
N
C
(
k
,
i
,
f
)
⋅
X
(
k
−
i
+
l
,
f
)
Y(k,f)=\sum_{i=0}^{N}C(k,i,f)·X(k-i+l,f)
Y(k,f)=i=0∑NC(k,i,f)⋅X(k−i+l,f)
其中
G
G
G是滤波器阶数为
N
N
N的复数系数,滤波器应用于输入频谱
X
X
X,
Y
Y
Y为增强频谱。在我们的框架中,Deep Filtering应用于 gain-enhanced spectrogram
Y
G
Y^G
YG。
l
l
l是一个可选的look-ahead(前瞻),如果
l
≥
1
l \geq1
l≥1,它允许将非因果抽头合并到线性组合中。此外,还可以在频率轴上进行过滤,允许合并相关性,例如重叠频带。
为了进一步保证Deep Filtering只影响周期部分,我们引入了一个学习到的加权因子
α
\alpha
α来生成最终输出频谱。
Y
D
F
(
k
,
f
)
=
α
(
k
)
⋅
Y
D
F
′
(
k
,
f
)
+
(
1
−
α
(
k
)
)
⋅
Y
G
(
k
,
f
)
Y^{DF}(k,f)=\alpha(k)·Y^{DF^{'}}(k,f)+(1-\alpha(k))·Y^{G}(k,f)
YDF(k,f)=α(k)⋅YDF′(k,f)+(1−α(k))⋅YG(k,f)
2.3. 框架概述
DeepFilterNet 算法的概述如图 1 所示。给定一个嘈杂(noisy)的音频信号 x ( t ) x(t) x(t),我们使用短时傅立叶变换 (STFT) 将信号转换到频域。 该框架处理 48 kHz 采样率的音频,以支持高分辨率 VoIP 应用程序和介于 4 ms 和 30 ms 之间的 STFT 窗口大小 N F F T N_{FFT} NFFT。 默认情况下,我们使用 N o v = 50 N_{ov}=50% Nov=50的重叠,但也支持低延迟场景的更高重叠。 我们为深度神经网络 (DNN) 使用两种输入特征。
- 对于 ERB 编码器/解码器特征 X E R B ( k , b ) , b ∈ [ 0 , N E R B ] X_{ERB}(k,b),b\in[0,N_{ERB}] XERB(k,b),b∈[0,NERB],我们计算对数功率谱,使用衰减为 1 s 的指数均值归一化(exponential mean normalization) [12],并应用具有可配置频段数目 N E R B N_{ERB} NERB的矩形 ERB 滤波器组 (FB)。
- 对于深度滤波器网络特征
Y
D
F
(
k
,
f
′
)
,
f
′
∈
[
0
,
f
D
F
]
Y^{DF}(k,f^{'}),f^{'}\in[0,f_{DF}]
YDF(k,f′),f′∈[0,fDF],我们使用复数谱作为输入,并使用具有相同衰减的指数单位归一化(Exponential Unit Normalization) [9] 对其进行归一化。

编码器/解码器体系结构用于预测ERB gain。利用逆ERB滤波器组将gain变换回频域维度,然后与噪声谱进行点乘。为了进一步增强周期分量,DeepFilterNet预测每频带滤波器系数
C
N
C^N
CN的阶数。我们只使用深度滤波器到频率
f
D
F
f_{DF}
fDF,假设周期成分包含大部分能量在较低的频率。
再加上卷积层的look-ahead和deep filter的look-ahead,得到整体延迟为
l
N
F
F
T
+
m
a
x
(
l
D
N
N
,
l
D
F
)
l_{N_{FFT}}+max(l_{DNN},l_{DF})
lNFFT+max(lDNN,lDF),结果在
N
F
F
T
=
240
N_{FFT}=240
NFFT=240时,最小延迟为
5
+
m
a
x
(
0
,
0
)
=
5
m
s
5 + max(0,0) = 5 ms
5+max(0,0)=5ms。
2.4. DNN模型
我们专注于设计一个只使用标准DNN(如卷积、批处理归一化、ReLU等)的高效神经网络,这样我们就可以利用层融合以及推理框架的良好支持。我们采用类似于[13,7]的UNet架构,如图2所示。我们的卷积块包含一个深度可分离卷积,核大小为(3x2), 通道C为64,然后是批归一化和ReLU激活。卷积层在时间上对齐,这样第一层可以引入一个整体的look-ahead
l
D
N
N
l_{DNN}
lDNN。我们在线性和GRU层中大量使用分组(grouping)[14,13]。分组输出被shuffle以恢复组间相关性,并再次concatenated(串联)到完全隐藏的大小。带有add skip connection的卷积pathways [13,7]用于保持频率分辨率。我们为DF Net使用了一个全局路径跳过连接,以在输出层提供原始噪声相位的良好表示。

2.5. 数据处理
DeepFilterNet框架利用大量的实时增强功能。我们在信噪比(SNR)为{-5,0,5,10,20,40}dB的情况下,将一个纯净的语音信号与多达5个噪声信号混合。为了进一步增加变量,我们使用二阶滤波器[1]、EQs和{-6,0,6}dB的随机增益来增强语音信号和噪声信号。随机重采样增加了音高的多样性,室内脉冲响应(RIR)用于模拟混响环境。如果语音信号的采样率低于当前模型的采样率,则在混合前对噪声信号应用低通滤波器。例如,这也允许在全频带音频(48 kHz)上训练的模型在低采样率的输入信号上同样表现良好。我们进一步支持训练衰减有限模型。因此,我们生成一个噪声目标信号 s s s,它的信噪比比噪声信号 x x x高6到20 dB。在训练期间,我们对预测增益 G G G进行clamp,并设定一个有噪声的目标 s s s,DFNet将学习不去除超过规定的噪声。这在可穿戴设备上很有用,因为我们想让用户保持一些环境意识。
2.6. 损失函数
提供理想的DF系数 C N C^N CN并非易事,因为有无限多的可能性[8]。相反,我们使用compressed(压缩)频谱损失来隐式学习ERB增益 G G G和滤波器系数 C N C^N CN[15,13]。
L s p e c = ∑ k , f ∥ ∣ Y ∣ c − ∣ S ∣ c ∥ 2 + ∑ k , f ∥ ∣ Y ∣ c e j φ Y − ∣ S ∣ c e j φ S ∥ 2 \mathcal{L}_{s p e c}=\sum_{k, f}\left\||Y|^{c}-|S|^{c}\right\|^{2}+\sum_{k, f}\left\||Y|^{c} e^{j \varphi_{Y}}-|S|^{c} e^{j \varphi_{S}}\right\|^{2} Lspec=k,f∑∥∣Y∣c−∣S∣c∥2+k,f∑ ∣Y∣cejφY−∣S∣cejφS 2
其中,
c
=
0.6
c=0.6
c=0.6是建模感知响度的压缩因子[16]。由于具有幅值和相位感知项,使得该损失既适用于建模实值增益,也适用于复数DF系数预测。为了使幅值接近于零的TF bin的梯度变硬(例如,对于采样率较低的输入信号),我们计算
φ
X
\varphi_X
φX的向后角度方法,如下所示:
δ
φ
δ
X
=
δ
X
⋅
(
−
ℑ
{
X
}
∣
X
h
∣
2
,
ℜ
{
X
}
∣
X
h
∣
2
)
\frac{\delta \varphi}{\delta X}=\delta X \cdot\left(\frac{-\Im\{X\}}{\left|X_{h}\right|^{2}}, \frac{\Re\{X\}}{\left|X_{h}\right|^{2}}\right)
δXδφ=δX⋅(∣Xh∣2−ℑ{X},∣Xh∣2ℜ{X})
式中
ℜ
{
X
}
\Re\{X\}
ℜ{X}和
ℑ
{
X
}
\Im\{X\}
ℑ{X}表示频谱X的实部和虚部,
∣
X
h
∣
2
=
m
a
x
(
ℜ
{
X
}
2
+
ℑ
{
X
}
2
,
1
e
−
12
)
|X_h|^2=max(\Re\{X\}^2+\Im\{X\}^2,1e^{-12})
∣Xh∣2=max(ℜ{X}2+ℑ{X}2,1e−12)平方数量级以避免被0除。
作为额外的损失项,我们强制DF分量只增强信号的周期性部分。动机如下。对于只有噪音的部分,DF不提供任何优于ERB增益的好处。DF甚至可能通过对周期性噪声(如发动机噪声或巴布噪声)进行建模而产生伪影,这在衰减受限模型中最为明显。此外,对于只有随机成分的语音,如摩擦音或爆破音,DF没有任何好处。假设,这些部分包含大部分的高频率能量,我们计算低于
f
D
F
f_{DF}
fDF频率的局部SNR。因此,
L
α
L_{\alpha}
Lα由下式给出:
L
α
=
∑
k
∥
α
⋅
1
L
S
N
R
<
−
10
d
B
∥
2
+
∑
k
∥
(
1
−
α
)
⋅
1
L
S
N
R
>
−
5
d
B
∥
2
,
\mathcal{L}_{\alpha}=\sum_{k}\left\|\alpha \cdot \mathbb{1}_{\mathrm{LSNR}<-10 \mathrm{~dB}}\right\|^{2}+\sum_{k}\left\|(1-\alpha) \cdot \mathbb{1}_{\mathrm{LSNR}>-5 \mathrm{~dB}}\right\|^{2},
Lα=k∑∥α⋅1LSNR<−10 dB∥2+k∑∥(1−α)⋅1LSNR>−5 dB∥2,
其中,当局部信噪比(LSNR)小于10 dB时,
I
LSNR
<
−
10
d
B
\mathbb{I}_{\text {LSNR }}<-10 \mathrm{~dB}
ILSNR <−10 dB为值为1的特征函数;当局部信噪比大于-5 dB时,
I
LSNR
>
−
5
d
B
\mathbb{I}_{\text {LSNR }}>-5 \mathrm{~dB}
ILSNR >−5 dB为1。在20ms窗口范围内,在频域中计算LSNR。综合损失由
L
=
λ
spec
⋅
L
spec
(
Y
,
S
)
+
λ
α
⋅
L
α
\mathcal{L}=\lambda_{\text {spec }} \cdot \mathcal{L}_{\text {spec }}(Y, S)+\lambda_{\alpha} \cdot \mathcal{L}_{\alpha}
L=λspec ⋅Lspec (Y,S)+λα⋅Lα
3. 实验
3.1. 训练步骤
我们基于深度噪声抑制(DNS)挑战数据集[10]训练我们的模型,该数据集包含超过750小时的全频带纯净语音和180小时的各种噪声类型。除了提供的在16 kHz采样的RIR外,我们使用image source模型[17]模拟了另外10 000个在48 kHz采样的RIR。我们将数据集分为train/validation/test(70/15/15%)。根据验证损失应用早期停止,结果在测试集中报告。Voice Bank/DEMAND测试集[18]用于比较DeepFilterNet与相关工作,如DCCRN(+)[11,7]和PercepNet[2]。
所有实验都使用采样率为48khz的全频带信号。我们取
N
N
R
B
N_{NRB}
NNRB= 32,
f
D
F
f_{DF}
fDF = 5 kHz,DF阶数N = 5,对DF和DNN卷积都取
l
=
1
l=1
l=1帧。我们用一个初始学习率为
1
∗
1
0
−
3
1*10^{-3}
1∗10−3的adam优化器,训练我们的模型在3 s样本和32个batch的30个epoch。学习率每3个epoch衰减0.9。损耗参数为
λ
s
p
e
c
=
1
\lambda_{spec} = 1
λspec=1和
λ
α
=
0.05
\lambda_\alpha = 0.05
λα=0.05。框架的源代码可以在 https://github.com/Rikorose/DeepFilterNet 获得。
3.2. 结果
我们评估了我们的框架在多种FFT大小上的性能,并基于尺度不变的信号失真率(SI-SDR)比较了DF和CRM的性能[19]。CRM是DF的特例,阶数
N
=
1
N=1
N=1,look-ahead
l
=
0
l=0
l=0。DNN前瞻对于CRM模型保持不变。
图3显示,在5 ms到30 ms的所有FFT大小中,DF都优于CRM。由于受到频率分辨率的限制,当FFT窗口大小为20 ms时,CRMs的性能会下降。另一方面,由于相邻帧间的相关性较小,DF相对恒定的性能下降了约30 ms。对于低延迟场景,将FFT重叠提高到75%会使DF和CRM的性能略有提高(输入SNR为0时,性能为+0.6 dB SI-SNR)。这种性能的提高可以解释为更高的帧内相关性,以及DNN更新RNN隐藏状态的步骤增加了一倍,但计算复杂度增加了一倍。图4给出了一个定性的例子,说明了DF重构噪声谱图中难以区分的语音谐波的能力。


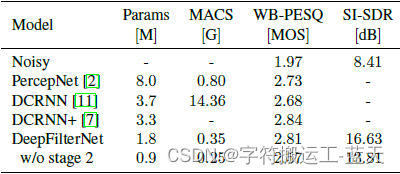
我们比较了使用NFFT=960 (20 ms)的DeepFilterNet和相关的工作,如PercepNet[2],它使用类似的感知方法,以及DCRNN+[7],它也使用深度滤波器。我们使用WB-PESSQ[20]评估语音增强的质量,并比较每秒乘法和累积(MACS)的计算复杂度。表1显示,DeepFilterNet优于PercepNet,性能与DCRNN+相当,同时具有更低的计算复杂度,使DeepFilterNet能够用于实时使用。
4. 结论
在这项工作中,我们提出了DeepFilterNet,一个低复杂度的语音增强框架。我们证明了深度过滤网的性能与其他算法相当,而计算量要求要低得多。我们进一步提供了深度过滤优于CRM的证据,特别是在较小的STF窗口大小的情况下。
5. 参考文献
[1] Jean-Marc Valin, A hybrid DSP/deep learning approach to real-time full-band speech enhancement, in 2018 IEEE 20th International Workshop on Multimedia Signal Processing (MMSP). IEEE, 2018, pp. 1 5.
[2] Jean-Marc Valin, Umut Isik, Neerad Phansalkar, Ritwik Giri, Karim Helwani, and Arvindh Krishnaswamy, A Perceptually-Motivated Approach for Low-Complexity, Real-Time Enhancement of Fullband Speech, in INTERSPEECH 2020, 2020.
[3] Xu Zhang, Xinlei Ren, Xiguang Zheng, Lianwu Chen, Chen Zhang, Liang Guo, and Bing Yu, Low-Delay Speech Enhancement Using Perceptually Motivated Target and Loss, in Proc. Interspeech 2021, 2021, pp. 2826 2830.
[4] Donald S Williamson, Monaural speech separation using a phase-aware deep denoising auto encoder, in 2018 IEEE 28th International Workshop on Machine Learning for Signal Processing (MLSP). IEEE, 2018, pp. 1 6.
[5] Ke Tan and DeLiang Wang, Complex spectral mapping with a convolutional recurrent network for monaural speech enhancement, in ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019, pp. 6865 6869.
[6] Jonathan Le Roux, Gordon Wichern, Shinji Watanabe, Andy Sarroff, and John R Hershey, Phasebook and friends: Leveraging discrete representations for source separation, IEEE Journal of Selected Topics in Signal Processing, vol. 13, no. 2, pp. 370 382, 2019.
[7] Shubo Lv, Yanxin Hu, Shimin Zhang, and Lei Xie, DCCRN+: Channel-wise Subband DCCRN with SNR Estimation for Speech Enhancement, in INTERSPEECH, 2021.
[8] Wolfgang Mack and Emanu el AP Habets, Deep Filtering: Signal Extraction and Reconstruction Using Complex Time-Frequency Filters, IEEE Signal Processing Letters, vol. 27, pp. 61 65, 2020.
[9] Hendrik Schr oter, Tobias Rosenkranz, Alberto Escalante Banuelos, Marc Aubreville, and Andreas Maier, CLCNet: Deep learning-based noise reduction for hearing aids using complex linear coding, in ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2020.
[10] Chandan KA Reddy, Harishchandra Dubey, Kazuhito Koishida, Arun Nair, Vishak Gopal, Ross Cutler, Sebastian Braun, Hannes Gamper, Robert Aichner, and Sriram Srinivasan, INTERSPEECH 2021 Deep Noise Suppression Challenge, in INTERSPEECH, 2021.
[11] Yanxin Hu, Yun Liu, Shubo Lv, Mengtao Xing, Shimin Zhang, Yihui Fu, Jian Wu, Bihong Zhang, and Lei Xie, DCCRN: Deep complex convolution recurrent network for phase-aware speech enhancement, in INTERSPEECH, 2020.
[12] Hendrik Schr oter, Tobias Rosenkranz, Alberto N. Escalante-B. , Pascal Zobel, and Andreas Maier, Lightweight Online Noise Reduction on Embedded Devices using Hierarchical Recurrent Neural Networks, in INTERSPEECH 2020, 2020.
[13] Sebastian Braun, Hannes Gamper, Chandan KA Reddy, and Ivan Tashev, Towards efficient models for real-time deep noise suppression, in ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2021, pp. 656 660.
[14] Ke Tan and DeLiangWang, Learning complex spectral mapping with gated convolutional recurrent networks for monaural speech enhancement, IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 28, pp. 380 390, 2019.
[15] Ariel Ephrat, Inbar Mosseri, Oran Lang, Tali Dekel, Kevin Wilson, Avinatan Hassidim, William T Freeman, and Michael Rubinstein, Looking to Listen at the Cocktail Party: A Speaker-Independent Audio-Visual Model for Speech Separation, ACM Transactions on Graphics (TOG), vol. 37, no. 4, pp. 1 11, 2018.
[16] Jean-Marc Valin, Srikanth Tenneti, Karim Helwani, Umut Isik, and Arvindh Krishnaswamy, Low- Complexity, Real-Time Joint Neural Echo Control and Speech Enhancement Based On PercepNet, in 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2021.
[17] Emanu el AP Habets and Sharon Gannot, Generating sensor signals in isotropic noise fields, The Journal of the Acoustical Society of America, vol. 122, no. 6, pp. 3464 3470, 2007.
[18] Cassia Valentini-Botinhao, Xin Wang, Shinji Takaki, and Junichi Yamagishi, Investigating RNN-based speech enhancement methods for noise-robust Text-to- Speech, in SSW, 2016, pp. 146 152.
[19] Jonathan Le Roux, Scott Wisdom, Hakan Erdogan, and John R Hershey, SDR half-baked or well done? , in ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2019, pp. 626 630.
[20] ITU, Wideband extension to Recommendation P.862 for the assessment of wideband telephone networks and speech codecs, ITU-T Recommendation P.862.2, 2007.