目录

位图

布隆过滤器

---

 

位图

假设有1000 万个范围在1~ 1亿的整数。如何快速查找某个整数是否出现在这1000万个整数中?
当然，这个问题仍然可以使用哈希表来解决。不过，针对这个“特殊”问题，我们可以使用一种比较“特殊”的哈希表，就是位图。
我们申请一个大小为1亿、数据类型为布尔类型(true 或者false)的数组，将这1000万个整数作为数组下标对应的数组元素值设置成true。例如，整数5包含在这1000万个整数中，我们就将下标为5的数组元素值设置为true,即array[5]=true。当要查询某个整数K是否在这1000万个整数中的时候，我们只需要将对应的数组值array[K]取出，查看是否等于true。 如果array[K]=true,那么说明这1000万个整数中包含这个整数K;如果array[K]=false,那么说明这1000万个整数中不包含这个整数K。
我们知道，表示true和false这两个布尔值，只需要用一个二进制位(bit)。 二进制位1表示true,二进制位0表示false。但是，在很多高级编程语言中，布尔类型占用1B大小的内存空间。对于位图，有没有更加节省内存的存储方式呢?
实际上，我们可以用一个char类型数据表示一个长度是8的位图8，同理，用char类型的a[n]数组表示长度是n*8的位图。在存取位图中的数据时，我们用数据除8，得到这个数据存储在哪个数组元素中后，用数据与8求余，得到数组存储在这个数组中的哪一个二进制位上。例如，对于26，与8相除得到的结果是3(商的部分)，也就是说，数据存储在a[3]这个数组元素上，然后，将26与8求余的结果是2，也就是说，数据存储在a[3]这个数组元素的第2个二进制位上。

template<size_t N>
class bitset
{
public:
	bitset()
	{
		_bits.resize(N / 8 + 1, 0);
	}
	void set(size_t x)
	{
		size_t i = x / 8;
		size_t ij = x % 8;
		_bit[i] |= (1 << j);
	}
	void reset(size_t x)
	{
		size_t i = x / 8;
		size_t ij = x % 8;
		_bits[i] &= ~(1 << j);
	}
	//检测某个数在不在
	bool get(size_t x)
	{
		size_t i = x / 8;
		size_t j = x % 8;

		return _bits[i] & (1 << j);
	}
private:
	vector<char> _bits;
};

因为位图通过数组下标来定位数据，所以访问效率非常高。而且，我们只需要用一个二进制位就能表示一个数字，在数字范围不大的情况下，相对于哈希表，位图这种数据结构非常节省内存。对于在100万个整数中查找数据这个问题，如果我们使用哈希表来存储这1000万个数据，那么大约需要40MB的内存空间。如果我们使用位图来存储这10000 万个数据，因为数字范围为1~1亿，所以只需要1亿个二进制位，也就是说，12MB左右的内存空间就足够了。

给定100万个整数，设计算法找到只出现一次的整数?

使用两个位图，出现0次，两个位图该数上的比特位都为0，出现1次，第一个位图上该数的比特位为0，第二个位图上该数的比特位为1，出现两次以上，两个位图该数上的比特位都为1.

template<size_t N>
class twobitset
{
public:
	void set(size_t x)
	{
		// 00 -> 01
		if (_bs1.test(x) == false
			&& _bs2.test(x) == false)
		{
			_bs2.set(x);
		}
		else if (_bs1.test(x) == false
			&& _bs2.test(x) == true)
		{
			// 01 -> 10
			_bs1.set(x);
			_bs2.reset(x);
		}
		// 10
	}
	//打印出只出现一次的值（第一个位图上该数的比特位为0，第二个位图上该数的比特位为1）
	void Print()
	{
		for (size_t i = 0; i < N; ++i)
		{
			if (_bs2.test(i))
			{
				cout << i << endl;
			}
		}
	}

public:
	bitset<N> _bs1;
	bitset<N> _bs2;
};

位图的应用

• 快速查找某个数据是否在一个集合中
• 排序 + 去重
• 求两个集合的交集、并集等
• 操作系统中磁盘块标记

优点：速度快、节省空间；缺点：只能映射整型。 

布隆过滤器

 不过，位图的应用场景有定的局限性， 就是数据所在的范围不能太大。如果数据所在的范围很大、如在1000万个整数中查找数据这个问题，数据范围不是1~1亿，而是1~10亿，那么位图就要占用10亿个二进制位，也就是120MB大小的内存空间，相比哈希表，内存占用不降反增。为了解决内存占用不降反增这个问题，我们对位图进行改进和优化，于是，布隆过滤器就产生了。

还是刚才提到的在1000万个整数中查找数据这个例子，数据个数是1000万，数据的范围变成了1~ 10亿。布隆过滤器的做法:尽管数据范围增大了，但我们仍然使用包含1亿个二进制位的位图。通过哈希函数对数据进行处理，让哈希值落在1~ 1亿这个范围内。例如，我们把哈希函数设计或简单的求余操作:f(x)=x%n其中，x表示数据，n表示位图的大小(这里是1亿)。我们知道，哈希函数存在冲突问题，对于100000001和1这两个数字，经过上面那个求余取模的哈希函数处理之后，最后的哈希值都是1，这就导致我们无法区分BitSet[1]=true表示的是1还是100000001了。

当然，为了降低冲突发生的概率，我们可以设计一个更复杂、更随机的哈希函数。除此之外，还有其他方法吗?我们看一下布隆过滤器的处理方法。既然一个哈希函数可能会存在冲突，那么使用多个哈希函数一起定位一个数据， 是否能降低冲突发生的概率呢?

我们使用K个哈希函数，分别对同一个数据计算哈希值，得到的结果分别记作X1,X2,X3,..,XK。我们把这K个哈希值作为位图的下标，将对应的BitSet[X1],BitSet[X2],BitSet[X3],...,BitSet[YK]都设置成true,也就是说，我们用K个二进制位而非一一个二进制位来表示一个数据是存在的。
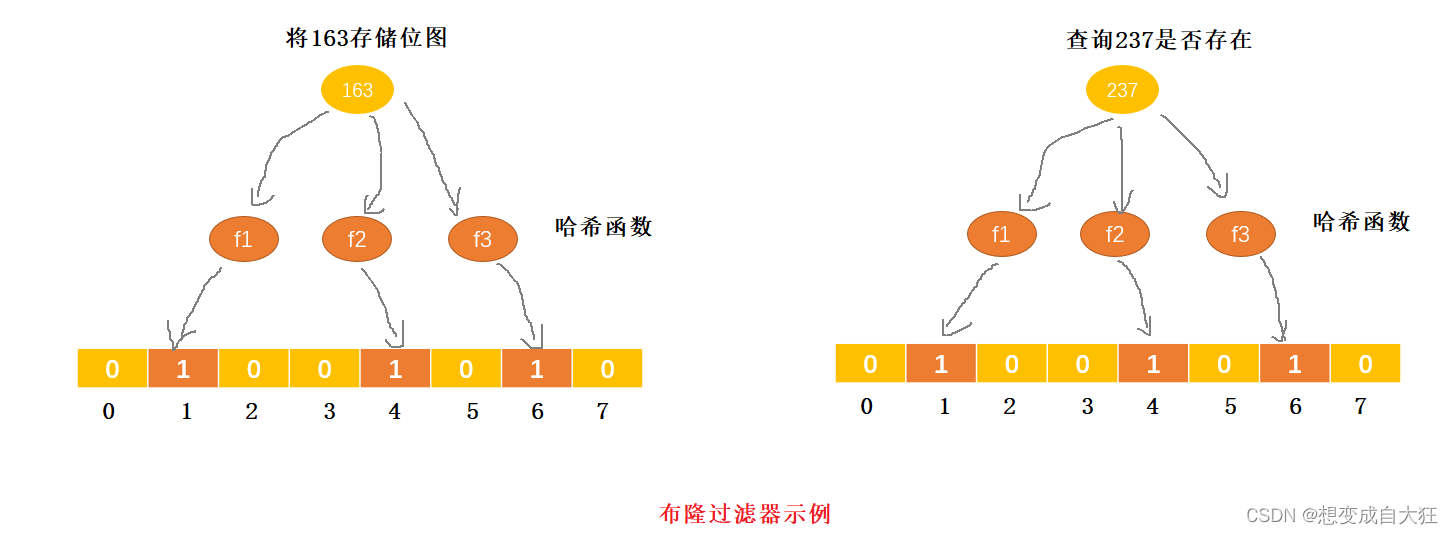
当要查询某个数据是否存在时，我们使用同样的K个哈希函数，分别对数据计算哈希值，得到Y1,Y2,Y3,..,YK，这K个值。我们用这K个哈希值作为下标，看对应位图中的数值是否都为true, 如果BitSet[Y1],BitSet[Y2],BitSet[Y3],...,BitSet[YK]都为tue,则说明这个数据存在； 如果其中任意一个不为true,就说明这个数据不存在。如图所示，数据163经过3个哈希函数计算之后，哈希值分别为1、4、6,因此，BitSet数组中下标为1、4、6的元素值设置为1。当要查询数据237是否存在时，将数据237经过3个哈希函数计算之后，哈希值分别为0、4、7,而在BitSet数组中，下标为0、4、7的元素值并非都为1，因此，判定数据237不存在。

实现代码： 

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (auto ch : s)
		{
			hash += ch;
			hash *= 31;
		}

		return hash;
	}
};

struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			size_t ch = s[i];
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
			}
		}
		return hash;
	}
};


struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};

// N最多会插入key数据的个数
template<size_t N,
	class K = string,
	class Hash1 = BKDRHash,
	class Hash2 = APHash,
	class Hash3 = DJBHash>
class BloomFilter
{
public:
	void set(const K& key)
	{
		size_t len = N * _X;
		size_t hash1 = Hash1()(key) % len;
		_bs.set(hash1);

		size_t hash2 = Hash2()(key) % len;
		_bs.set(hash2);

		size_t hash3 = Hash3()(key) % len;
		_bs.set(hash3);
	}

	bool test(const K& key)
	{
		size_t len = N * _X;

		size_t hash1 = Hash1()(key) % len;
		if (!_bs.test(hash1))
		{
			return false;
		}

		size_t hash2 = Hash2()(key) % len;
		if (!_bs.test(hash2))
		{
			return false;
		}

		size_t hash3 = Hash3()(key) % len;
		if (!_bs.test(hash3))
		{
			return false;
		}
		return true;
	}
private:
	static const size_t _X = 6;
	bitset<N* _X> _bs;
};

 对于两个不同的数字，经过一个哈希函数处理之后，可能会产生相同的哈希值。但是，经过K个哈希函数处理之后，K个哈希值都相同的概率就非常低了。不过，这种处理方式又带来了新的问题，那就是容易产生误判。如图所示，数据146、196 存储到BitSet数组之后，下标为0、2、3、4、6、7的元素值设置为1。当要查询数据177是否存在时，经过3个哈希函数计算之后，哈希值分别是1、2、7, 尽管数据177不存在，但BitSet数组中下标为1、2、7的元素值都为1，因此，就会误判为数据177存在。

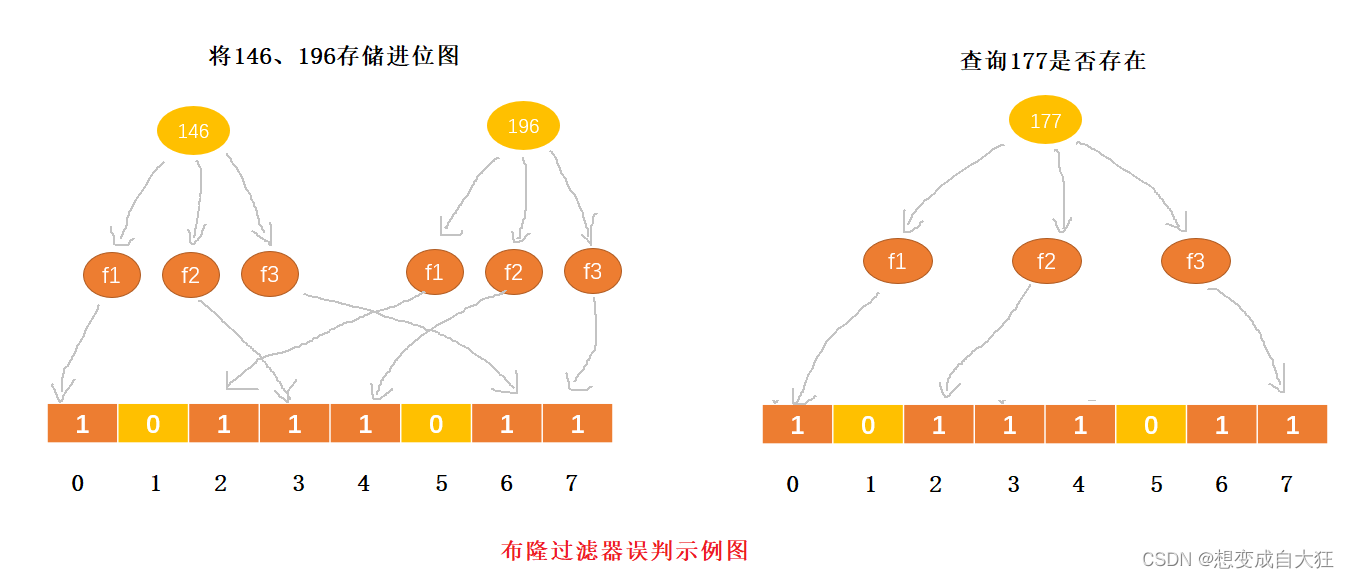
布隆过滤器的误判有一个特点: 只有在判断其存在的情况下，才有可能发生误判，也就是说。判定为存在时有可能并不存在。如果某个数据经过布隆过滤器后判断为不存在，就说明这个数据是真的不存在，这种情况是不会存在误判的。
尽管布隆过滤器会存在误判，但是，这并不影响它发挥大的作用。很多业务场景对误判有一定的容忍度。 例如“爬虫”中的网址链接判重问题，即便一个没有被爬取过的网页，被误判为己经被爬取。对于搜索引擎，也并不是什么大事情，是可以容忍的，毕竟网页太多了，搜索引擎也不可能完全爬取到。而且，只要我们调整哈希函数的个数、位图大小与要存储数据的个数的比例，就可以将这种误判的概率降到非常低。
除此之外，我们还可以利用布隆过滤器在到定数据不存在的情况下不会出现误判的特点，在访问数据库进行数据查询前，先访问布隆过滤器，如果经过布隆过速器后判定数据不特在，就不需要继续访问数据库了，这样就能减少数据库查询操作。

扩展BloomFilter使得它支持删除元素的操作

布隆过滤器不能直接删除，会导致存在的元素误判为找不到，可以用多个比特位表示，删除就让比特位减1。