作为一款接口调试利器, Postman的更新迭代速度很快, 不断加入了很多新的功能.使的api设计,测试,监控, Mock,以及团队协作更加方便.
修改执行顺序
在遇到有接口依赖的情况, 我们往往需要接口按顺序执行, 之前可以通过在一个请求的Pre-request Scripts中使用pm.sendRequest发送所依赖的请求来实现, 新版本Postman在Run Collection中我们可以修改请求的执行顺序, 如下图:

这里将所有的接口放到一个Collection请求集合中, 在"百度获取token"这个请求的Tests脚本中中,将access_token存为全局变量, 以供"百度orc"使用.
我们可以直接拖动, 改变默认Collection的执行顺序, 也可以选择不运行哪些请求.
Workflow工作流
除了在Run Collection时调整顺序外,我们还可以通过postman.setNextRequest("同Collection下保存的请求名");来手动控制请求的跳转.
顺序结构
如下图, 新建一个Collection, 新增A, B, C, D, E, F 5个请求, 在请求A的Tests脚本中添加
postman.setNextRequest("D");以使A执行完下一个执行D请求.



从上图我们可以看出, 实际上跳过了请求B, C, 直接跳转到D请求.
注意: 如果D请求在运行时未勾选, 则只会运行A请求
分支结构
通常情况下,我们可以使用if判断来控制流程跳转, 比如, 通过判断A请求是否成功来分别跳转到D请求或B请求.
var jsonData = pm.response.json()
if(jsonData.args.a == 'a'){
postman.setNextRequest("D");
}
else{
postman.setNextRequest("B");
}循环结构
我们可以通过在最后一个请求中使用postman.setNextRequest(), 之前的请求, 来完成一个循环, 比如在F请求使用postman.setNextRequest("A"), 就会无限循环的执行下去, 如下图所示:

一般来说, 循环中一定要设置中止条件, 一般通过if判断是否postman.setNextRequest()来控制是否继续循环.
示例: 异步接口轮询
我们可以用一个postman.setNextRequest指向自身的请求来完成异步接口的轮询.
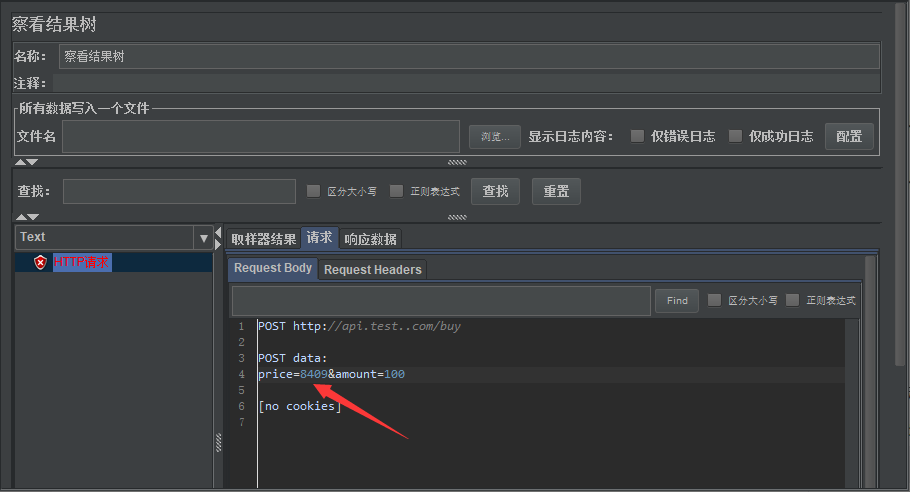
- 新建一个Collection, 新建一个"创建订单接口", 请求为:
http://115.28.108.130:5000/api/order/create/?
user_id=123&goods_id=123&num=2&amount=20.0这是一个异步接口, 接口会返回一个order_id用于查询订单结果. 我们在Tests中,将获取到的order_id存为全局变量以供下一个接口使用, 如下图所示:
var jsonData = pm.response.json()
pm.globals.set("order_id", jsonData.order_id);
- 新建一个"获取订单结果"接口, 请求为:
http://115.28.108.130:5000/api/order/get_result/?order_id={{order_id}}这是一个获取订单接口, 订单不确定多长时间创建好, 如果订单在创建过程中则返回"{}", 如果创建成功则返回:
{
"amount": "20.0",
"goods_id": "123",
"num": "2",
"user_id": "123"
}我们在Tests脚本中设置轮询条件, 下个请求指向自身如下:
if(pm.response.text() == "{}\n"){
postman.setNextRequest("获取订单结果");
}Run Collection 我们发现, "获取订单结果"请求被快速的请求, 直到停止, 实际上我们还需要设置一个轮询间隔, 我们将postman.setNextRequest放到一个函数种,然后用setTimeout来延迟一定时间运行.
function loop(){
postman.setNextRequest("获取订单结果")
}
if(pm.response.text() == "{}\n"){
setTimeout(loop, 5000); // 设置间隔5s
}如下图, "获取订单结果"请求会5妙执行一次, 知道订单处理完成.

注意:
- 一般我们还要设置最大轮询次数或最大轮询时间, 来防止接口始终返回"{}\n", 导致轮询无法中止(可以通过使用整数变量自增完成).
- 在轮询完也可以加上断言(写到else中)
实战案例
光学理论是没用的,要学会跟着一起敲,要动手实操,才能将自己的所学运用到实际当中去,这时候可以搞点实战案例来学习。


如果对你有帮助的话,点个赞收个藏,给作者一个鼓励。也方便你下次能够快速查找。
如有不懂还要咨询下方小卡片,博主也希望和志同道合的测试人员一起学习进步
在适当的年龄,选择适当的岗位,尽量去发挥好自己的优势。
我的自动化测试开发之路,一路走来都离不每个阶段的计划,因为自己喜欢规划和总结,
测试开发视频教程、学习笔记领取传送门!!!