高通滤波和低通滤波理性到感性分析

高通低通滤波辨析

• 物理意义：
  • 从频率角度，高通滤掉低频信息，低通滤掉高频信息
  • 从采样点看，低通使样点前后变化更平缓，也即增大低频，降低高频
• 总体说明
  • 本质是对当前维度的样点值，进行平滑，去除相关高低频率的信息
  • 时域越平缓，对应的低频信息越多；时域越变化，对应的高频信息越多
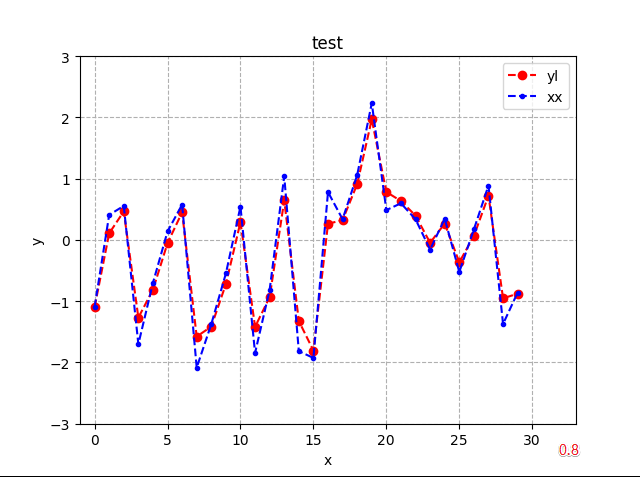
• 低通（1阶）
  • alpha参数，从0-1变化，0则无滤波效果全为初始值x[0]，1则全为x[i]输入
  • 0.1低通最狠，0.8低通稍轻
  • 总体是压低样点前后间的变化，光滑曲线减少变化，拉得更像一条直线
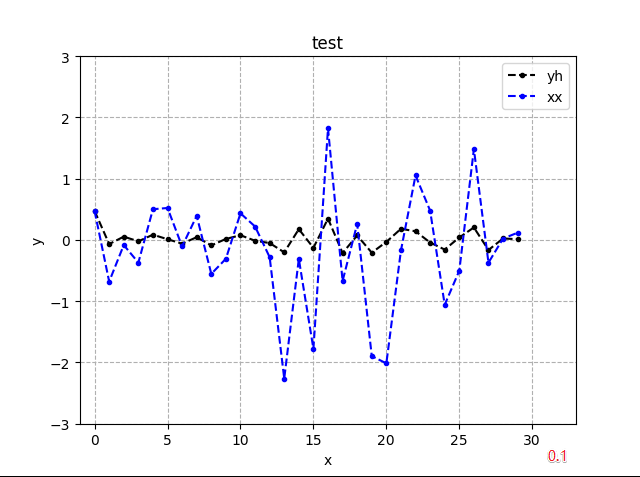
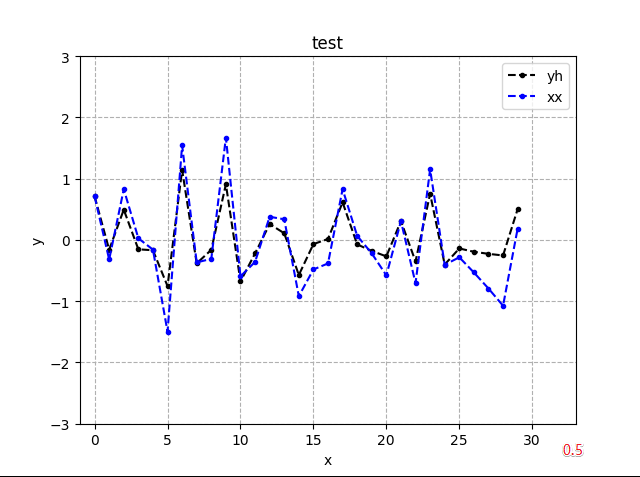
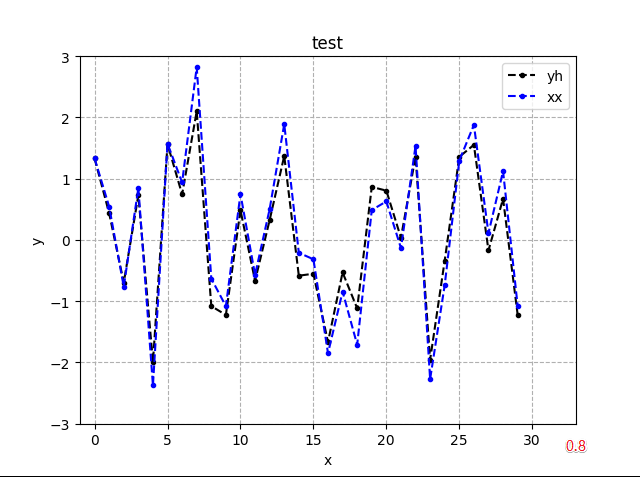
• 高通（1阶）
  • 总体是在压低振幅范围，包络前后变化不明显
  • 0.1高通最狠，0.8高通稍轻
  • 样点间变的小幅密集，实现高通，平缓变化被减弱，从而阻止低通

公式如下图：

低通滤波参数对比：

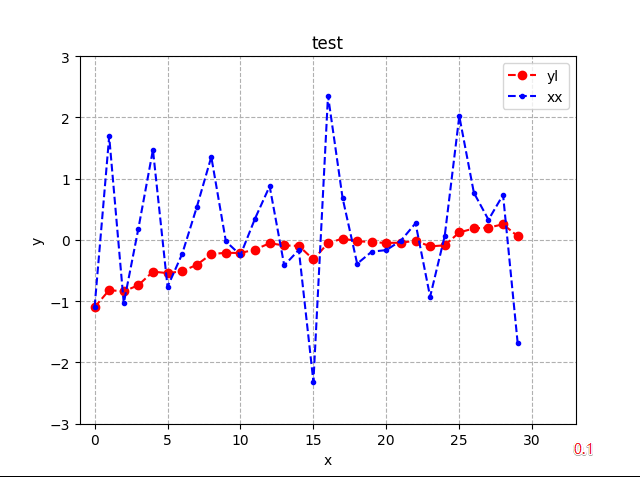
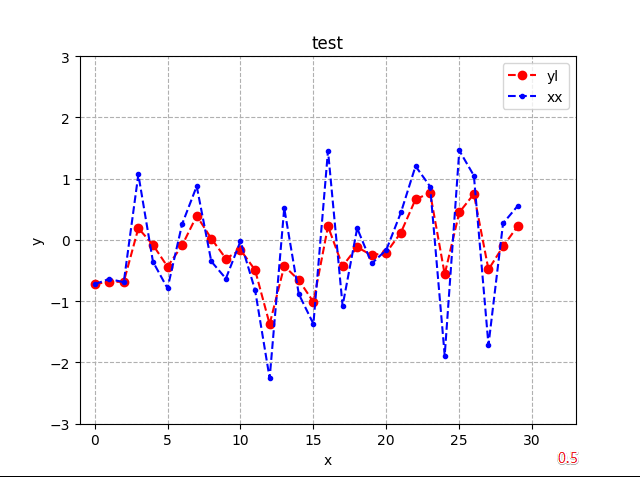
高通滤波参数对比：

Python仿真代码

编码进行对比分析：

# -*- coding: utf-8 -*-
"""
Created on Thu Jul  7 14:09:06 2022

@author: laizhixiao
"""

import matplotlib.pyplot as plt      # 绘图用
import numpy as np                   # 数据处理用
import math as mt                    # 数学运算


def plot_advance(x, y0, y1, xx):
    fig2 = plt.figure()
#    l1 = plt.plot(x, y0, color='r',marker='o', linestyle='dashed', label='yl')   # 返回结果为对线操作的句柄
    l2 = plt.plot(x, y1, color='k',marker='.', linestyle='--', label='yh')        # 黑色，linestye: -, --实线
    l2 = plt.plot(x, xx, color='b',marker='.', linestyle='--', label='xx')        # 黑色，linestye: -, --实线
    
    plt.xlabel('x')
    plt.ylabel('y')
    plt.title('test')
    plt.legend()                             # 显示图例，即每条线对应 label 中的内容
#     plt.axis([-1, 33, -1, 480])            # [xmin, xmax, ymin, ymax]
    plt.xlim(-1, 33)                         # 或单独设置
    plt.ylim(-3, 3)
#     plt.grid()
    plt.grid(linestyle='--')               # 组合有： -.   -- 
    plt.show()
#    plt.savefig('./salary.jpg')
    fig2.savefig('./pic.jpg')
    # plt.close(fig2)


if __name__ == "__main__":
    x0 = list(range(30))
    x  = np.random.randn(30)

    #lowpass
    yl = list(range(30))
    yl[0] = x[0]
    alpha = 0.8
    for i in range(29):
        i = i + 1
        yl[i] = alpha * x[i] + (1 - alpha) * (yl[i - 1])

    #highpass
    yh = list(range(30))
    yh[0] = x[0]
    for i in range(29):
        i = i + 1
        yh[i] = alpha * yh[i - 1] + alpha * (x[i] - x[i - 1])

    print('start processing...')
    plot_advance(x0, yl, yh, x)
    print('done!')

参考资料

---

1. 高通滤波与低通滤波的简单理解，link1
2. 低通滤波器和高通滤波器的程序实现原理推导，link2