(AVL)平衡二叉树

news2024/11/15 8:48:18

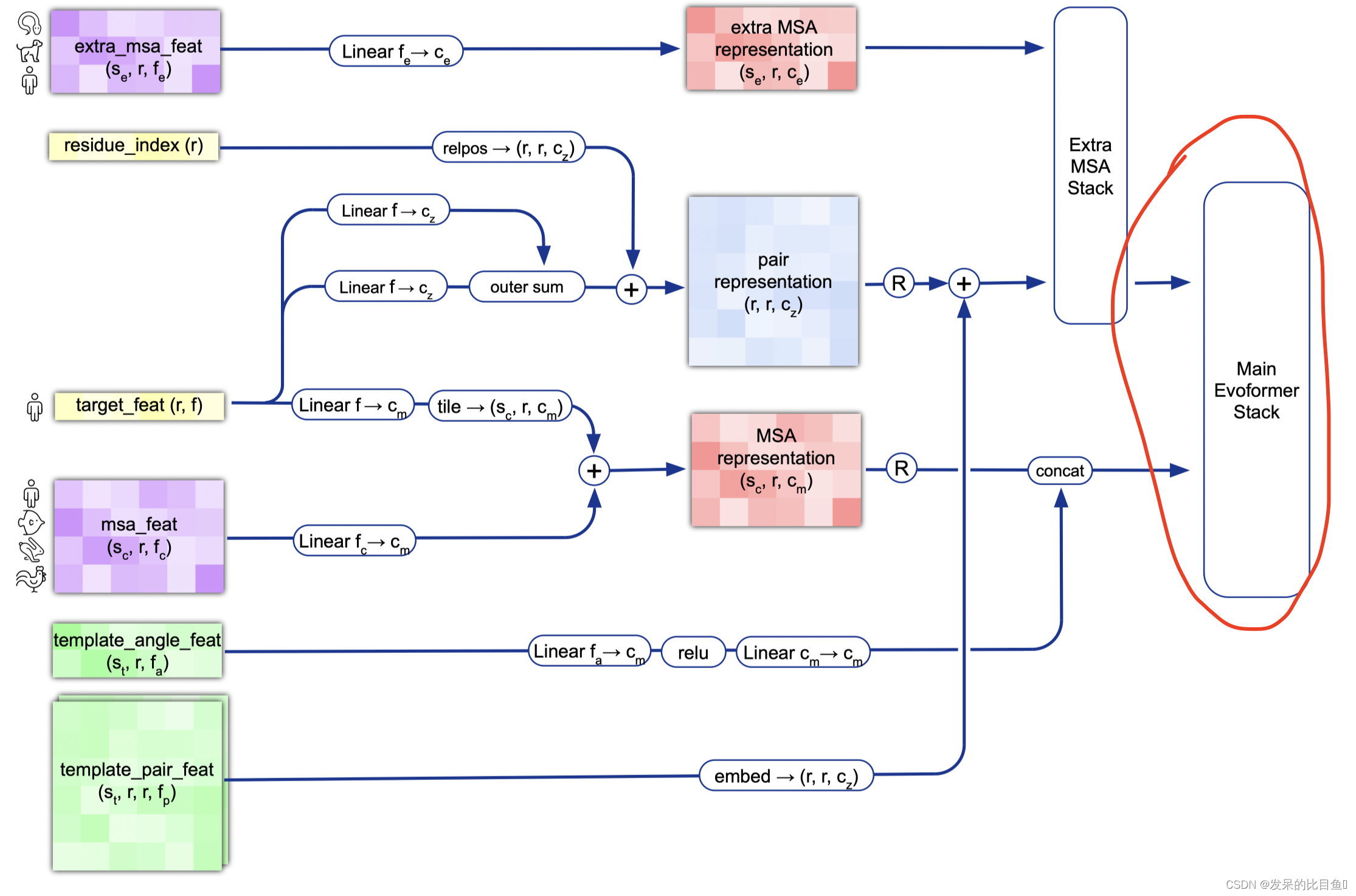
还是照旧，本篇主要讲一下代码实现，AVL相关的定义什么的这里不多赘述。

AVL树就是为了解决bst树出现了“线性”的问题，而发明的。什么是线性的就是一棵bst树全都只有左子树或者全都只有右子树，能想象来吧。

目录

 LL型调整(左旋)

RR型调整（右旋）

LR调整

RL调整

 代码实现：

因此呢AVL树一定是一棵bst树。不了解bst的可以先看看我这篇文章：(BST) 二叉排序树

AVL树是一类特殊的二叉排序树，它或者为空树，或者其左右子树都是平衡二叉排序树，而且其左右的子数高度之差绝对值不超过1.为了保证相对平衡，每次插入元素都会做相应的旋转

上面说了为了让avl树能保持平衡，每次插入节点后不平衡了就需要调整，旋转。

 这样的话就衍生出来了avl的四种旋转方式，四种旋转方式搞懂了，avl的创建就没问题了 

下面说说四种调整方式

 LL型调整(左旋)

A的左孩子的左孩子插入新的节点，导致A的平衡因子从1变为2，不在满足根本性质[-1,1]，所以需要通过旋转。显然，按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，这样看来，仿佛A结点绕结点B顺时针旋转一样。

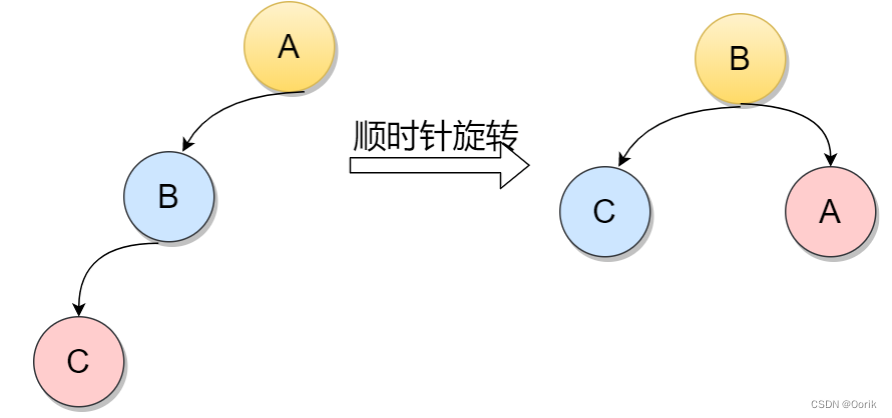
当在节点5的左子树中插入节点的时候而导致不平衡。这种情况调整如下：首先将元素5的左孩子2提升为新的根结点；然后将原来的根结点元素5变为元素2的右孩子；其他各子树按大小关系连接。

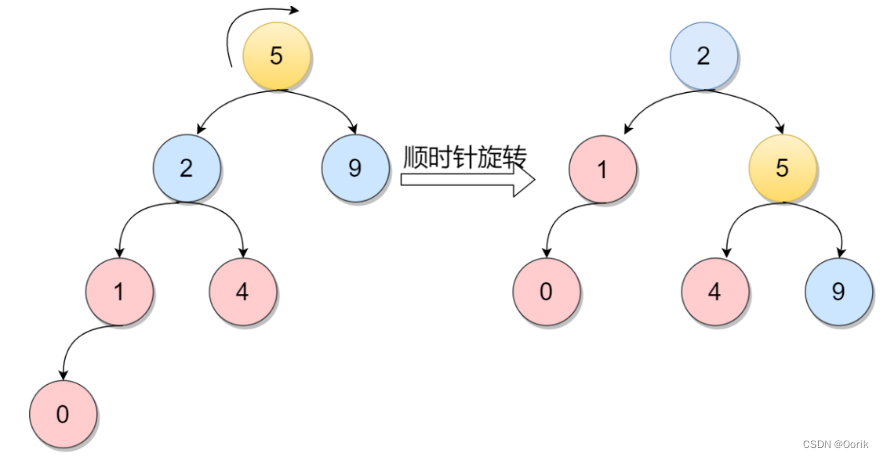
RR型调整（右旋）

在元素5的右孩子的右孩子插入新的节点，导致元素5的平衡因子从-1变为-2，不在满足根本性质[-1,1]，所以需要通过旋转。显然，按照大小关系，结点元素7应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，这样看来，仿佛节点元素5绕结点元素7逆时针旋转一样。

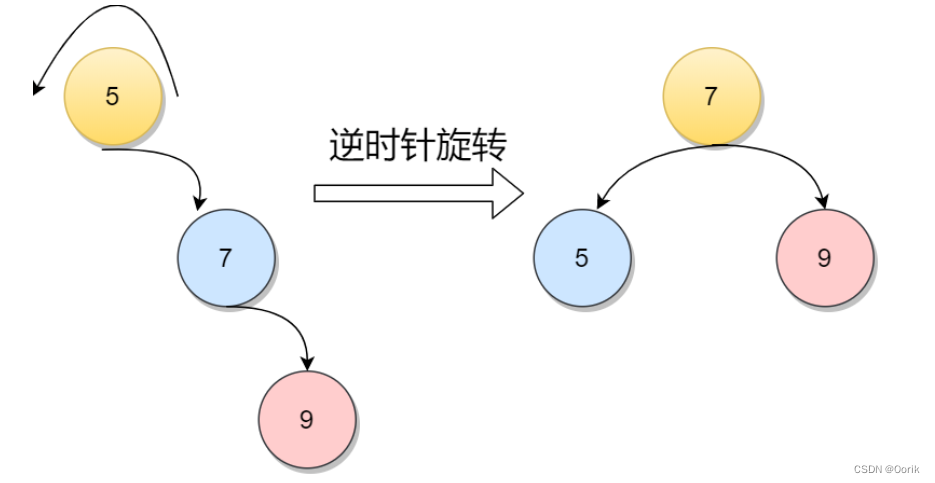
LR调整

节点元素5的左孩子的右子树上插入新节点，导致不平衡。此时元素5的平衡因子由1变为2。第一张图是LR型的最简单形式。显然，按照大小关系，元素3应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。

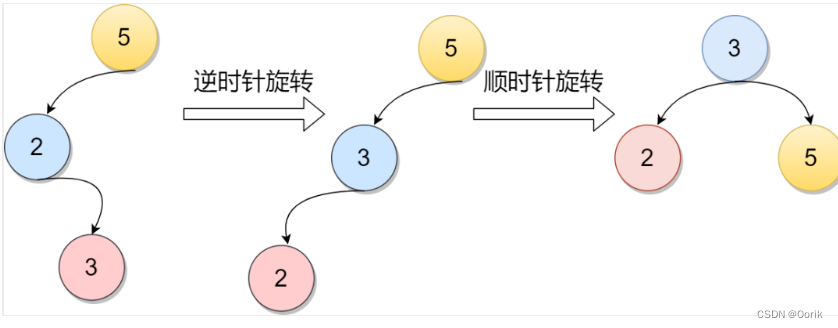
节点元素6增加一个左孩子，导致元素4变得不平衡。先顺时针旋转元素7再逆时针旋转4元素达到平衡。 

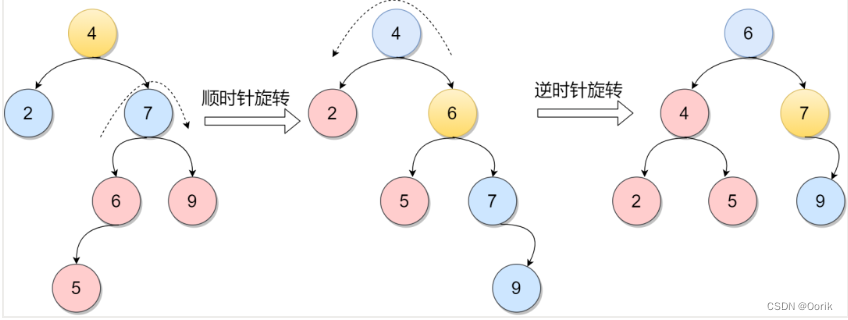
RL调整

当在元素5的右孩子的左子树增加一个节点7的时候，会造成不平衡的情况。先逆时针旋转成RR情况，再将元素5顺时针旋转。

 第二种情况方法类似，看起来会复杂一点。当在元素7得左孩子6增加左孩子元素5得时候，导致元素4变得不平衡。那么先顺时针调整元素7，再逆时针调整元素4

 代码实现：

主类大概这样：

class AVLNode {
public:
	AVLNode():m_left(nullptr),m_right(nullptr),m_bf(0){}
	AVLNode(int v):m_value(v), m_left(nullptr), m_right(nullptr), m_bf(0) {}
	int m_value;
	AVLNode *m_left;
	AVLNode *m_right;
	int m_bf;//平衡因子，该结点左右子树高度(深度)差
};
class AVLTree {
public:
	AVLTree() :m_root(nullptr){}
	void InsertAVLTree(int v) 
	{
		InsertAVLTree(m_root, v);
	}
	//传指针 再引用直接就在原来的树上修改了
	
	//斜线       
	void RotateRR(AVLNode*& t);//右旋
	void RotateLL(AVLNode*& t);//左旋
	//折线
	void RotateRL(AVLNode*& t);//右左旋
	void RotateLR(AVLNode*& t);//左右旋

	void InsertAVLTree(AVLNode* &t, int v);//插入
	void DelAVLTree(int key);//删除当前key这个值

	void TTer(AVLNode*& t);//中序遍历
	AVLNode* m_root;
};

四个调整函数：

void AVLTree::RotateLL(AVLNode*& t)
{
	AVLNode* child = t;
	t = child->m_right;
	child->m_right = t->m_left;
	t->m_left = child;
	t->m_bf = child->m_bf = 0;
}
void AVLTree::RotateRR(AVLNode*& t)
{
	AVLNode* child = t;
	t = child->m_left;
	child->m_left = t->m_right;
	t->m_right = child;
	t->m_bf = child->m_bf = 0;
}
void AVLTree::RotateRL(AVLNode*& t)
{
	AVLNode* childL = t;
	AVLNode* childR = t->m_right;
	t = childR->m_left;
	//先右旋
	//将t的右孩子作为childR的左孩子，childR作为t的右孩子
	childR->m_left = t->m_right;
	t->m_right = childR;
	if (t->m_bf >= 0) {
		childR->m_bf = 0;
	}
	else {
		childR->m_bf = 1;
	}
	//再左旋
	childL->m_right = t->m_left;//左子树
	t->m_left = childL;
	if (t->m_bf==1) {
		childL->m_bf = -1;
	}
	else {
		childL->m_bf = 0;
	}
	t->m_bf = 0;
}
void AVLTree::RotateLR(AVLNode*& t)
{
	AVLNode* childR = t;
	AVLNode* childL = t->m_left;
	t = childL->m_right;
	//先左旋
	childL->m_right = t->m_left;//左子树
	t->m_left = childL;
	if (t->m_bf <= 0)
	{
		childL->m_bf = 0;
	}
	else
	{
		childL->m_bf = -1;
	}
	//再右旋
	childR->m_left = t->m_right;//右子树
	t->m_right = childR;
	if (t->m_bf ==-1)
	{
		childR->m_bf = 1;
	}
	else
	{
		childR->m_bf = 0;
	}
	t->m_bf = 0;
}

AVL的插入创建

void AVLTree::InsertAVLTree(AVLNode*& t, int v)
{
	
	AVLNode* p = t;
	AVLNode* parent = nullptr;
	stack<AVLNode*>sk;//存储路径上的所有节点
	while (p != nullptr) {
		if (p->m_value == v) {
			return;
		}
		parent = p;
		sk.push(parent);//入栈为计算插入新节点后路径上父辈的bf
		if (v < p->m_value)
		{
			p = p->m_left;
		}
		else
		{
			p = p->m_right;
		}
	}
	//用v生成新节点
	p = new AVLNode(v);
	if (parent == nullptr)
	{
		t = p;
		return;
	}
	//将p链接到树中对应的位置
	if (v < parent->m_value) {
		parent->m_left = p;
	}
	else {
		parent->m_right = p;
	}
	//计算bf
	while (!sk.empty())
	{
		parent = sk.top();
		sk.pop();
		//这里我们用右边减左边来算
		if (parent->m_left == p)//如果此时p插到了parent的左边
		{
			parent->m_bf--;
		}
		else
		{
			parent->m_bf++;
		}

		if (parent->m_bf == 0)//一定平衡着,高度没有发生变化
		{
			/*  bf
			   -1     3
				0   2
				插入个4变成了
				0     3
				0   2   4
			*/
			break;
		}
		if (abs(parent->m_bf) == 1)
		{//如果插入后bf绝对值等于1
		 //那么有可能不平衡，需要往上看
			p = parent;
		}
		else
		{
			//父结点的bf绝对值为2，此时作为最小不平衡子树，开始旋转
			int flag = parent->m_bf > 0 ? 1 : -1;
			if (p->m_bf == flag)//斜线,同号
			{
				if (flag == -1)//右旋	
					RotateRR(parent);
				else//左旋		
					RotateLL(parent);
			}
			else 
			{
				//折线，不同号
				if (flag == 1)//右高，先右旋再左旋
				{
					RotateRL(parent);
				}
				else
				{
					//先左旋再右旋
					RotateLR(parent);
				}
				
			}	
			break;
		}
	}
		//旋转后需要进行调整，
		if (sk.empty())//此时栈空了说明不用链接了
		{
			t = parent;
		}
		else
		{
			AVLNode* q = sk.top();
			if (q->m_value > parent->m_value)//栈顶大于parent，往左链接
			{
				q->m_left = parent;
			}
			else
			{
				q->m_right = parent;
			}
		}
}

AVL删除特定值节点

void AVLTree::DelAVLTree(int k)//删除当前key这个值
{
	AVLNode* p = m_root;
	AVLNode* parent = NULL, * ppr = NULL;
	stack<AVLNode*> st;
	while (p)
	{
		if (p->m_value == k)
			break;
		parent = p;
		st.push(parent);
		if (k < p->m_value)
			p = p->m_left;
		else
			p = p->m_right;
	}
	if (p == NULL)
		return;
	AVLNode* q = NULL;
	if (p->m_left != NULL && p->m_right != NULL)
	{
		parent = p;
		st.push(parent);
		q = p->m_left;
		while (q->m_right != NULL)
		{
			parent = q;
			st.push(parent);
			q = q->m_right;
		}
		//替换
		p->m_value = q->m_value;
		p = q;
	}
	if (p->m_left != NULL)
		q = p->m_left;
	else
		q = p->m_right;
	int f; //标记删除的是左孩子0，右孩子1
	if (parent == NULL)
		m_root = parent;
	else
	{
		if (parent->m_left == p)
		{
			parent->m_left = q;
			f = 0;
		}
		else
		{
			parent->m_right = q;
			f = 1;
		}
		//删除完后调整bf
		//根据栈中存储的路径计算bf
		int link;
		while (!st.empty())
		{
			parent = st.top();
			st.pop();
			if (parent->m_right == q && f == 1)
				parent->m_bf--;
			else
				parent->m_bf++;
			if (!st.empty())
			{
				//保存旋转之前的父节点，为了旋转后链接
				ppr = st.top();
				link = (ppr->m_left == parent) ? -1 : 1;
			}
			else
				link = 0;
			if (parent->m_bf == -1 || parent->m_bf == 1)
				break;
			if (parent->m_bf == 0)
				q = parent;
			else
			{
				//旋转
				int flag = 0;
				if (parent->m_bf < 0)
				{
					flag = -1;
					q = parent->m_left;
				}
				else
				{
					flag = 1;
					q = parent->m_right;
				}
				if (q->m_bf == 0)//单
				{
					if (flag == -1)//左高
					{
						RotateRR(parent);
						parent->m_bf = 1;
						parent->m_right->m_bf = -1;
					}
					else
					{
						RotateLL(parent);
						parent->m_bf = -1;
						parent->m_left->m_bf = 1;
					}
					break;
				}
				if (q->m_bf == flag)
				{
					if (flag == -1)
						RotateRR(parent);
					else
						RotateLL(parent);
				}
				else
				{
					if (flag == -1)
						RotateLR(parent);
					else
						RotateRL(parent);
				}
				if (link == -1)
					ppr->m_left = parent;
				else if (link == 1)
					ppr->m_right = parent;
			}
		}
		if (st.empty())
			m_root = parent;
	}
	delete p;
	p = NULL;
}

写个简单的中序遍历，用来打印测试一下，因为bst树中序是从小到大排序的，那avl中序必然也是有序的

void AVLTree::TTer(AVLNode*& cur) {
	if (cur == nullptr)return;
	TTer(cur->m_left);
	cout << cur->m_value << " " ;
	TTer(cur->m_right);
}

写个测试：

int  main()
{
	vector<int>nums{ 3,2,1,4,5,6,7,10,9,8 };
	AVLTree t;
	for (const auto& x : nums)
	{
		t.InsertAVLTree(x);//插入
	}
	t.TTer(t.m_root);//写个中序 遍历出来从小到大
	t.DelAVLTree(5);//删除个5
	cout << endl;
	t.TTer(t.m_root);
	return 0;
}

ok完事收工

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/56890.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

HTML5期末考核大作业、HTML个人主页界面设计源码

HTML5期末考核大作业、HTML个人主页界面设计源码

&#x1f389;精彩专栏推荐&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb;&#x1f447;&#x1f3fb; ✍️ 作者简介: 一个热爱把逻辑思维转变为代码的技术博主 &#x1f482; 作者主页: 【主页——&#x1f680;获取更多优质源码】 &#x1f393; web前端期末大作业…
阅读更多...
uniapp 中 vuex 的使用

uniapp 中 vuex 的使用

1. uniapp 中 vuex 的介绍 2. uniapp 中 vuex 的使用 3. require.context 介绍 4. vuex 模块分离 5. vuex 模块分离 - 代码优化 1. uniapp 中 vuex 的介绍 uniapp 内置了 vuex&#xff0c;不需像 vue 脚手架那样里通过 npm 安装了&#xff0c;我们只需要引用就行了 2. un…
阅读更多...
会员接口治理的探索与实践

会员接口治理的探索与实践

随着爱奇艺会员破亿&#xff0c;会员服务从小而快的单一业务系统升级为了按领域划分的微服务模式&#xff0c;满足了业务的高速发展和服务的高流量调用&#xff0c;但是微服务的拆分&#xff0c;系统间的交互越来越多&#xff0c;在需求开发时&#xff0c;协作成本随之增加&…
阅读更多...
[激光原理与应用-30]：典型激光器 -2- 气体激光器 （连续激光器）

[激光原理与应用-30]：典型激光器 -2- 气体激光器 （连续激光器）

目录 第1章 概览 1.1 什么气体激光器 1.2 主要激励方式 1.3 发展历程 1.4 组成 1.5 特点 第2章 气体激光器分类 2.1 原子气体激光器 2.2 离子气体激光器 2.3 分子气体激光器 2.4 准分子激光器 第1章 概览 1.1 什么气体激光器 气体激光器利用气体作为工作物质产生激…
阅读更多...
AlphaFold2源码解析(6)--模型之特征表征

AlphaFold2源码解析(6)--模型之特征表征

AlphaFold2源码解析(6)–模型之特征表征 整体推理说明&#xff1a; Embedding只是在推理使用&#xff0c;影响非常小&#xff08;sup-Inference篇章&#xff09; 特征表征表示的入口模型如下&#xff1a; evoformer_module EmbeddingsAndEvoformer(self.config.embeddings_…
阅读更多...
亚马逊卖家店铺没流量怎么办？这几个方法可以试试！

亚马逊卖家店铺没流量怎么办？这几个方法可以试试！

大家都知道亚马逊是一个产品为王的平台&#xff0c;只有我们的产品好&#xff0c;亚马逊就会给我们推送流量&#xff0c;作为一个新手卖家该如何帮亚马逊店铺来获取流量&#xff0c;今天赛狐ERP就来给卖家们几个方法&#xff0c;来获取流量。 1.自然搜索 自然流量顾名思义也就…
阅读更多...
docker搭建测试，镜像保存并传输发布

docker搭建测试，镜像保存并传输发布

Docker OPENJDK本身的docker占用526M &#xff0c;昨天我在本地测试的&#xff0c;加上我们的项目大小&#xff0c;最终创建的镜像大小大概是526M项目大小&#xff0c;镜像大小大概这么多&#xff0c;我们需要先在服务器上安装docker&#xff0c;之后安装dockerOpenJDK&#x…
阅读更多...
LIO-SAM源码解析（四）：imuPreintegration.cpp

LIO-SAM源码解析（四）：imuPreintegration.cpp

1. 代码流程 2. 功能说明 这个cpp文件主要有两个类&#xff0c;一个叫IMUPreintegration类&#xff0c;一个叫TransformFusion类。 现在我们分开讲&#xff0c;先说IMUPreintegration类。 关于IMU原始数据&#xff0c;送入imuhandle中&#xff1a; 2.1. imuhandle imu原始…
阅读更多...
re:Invent现场直击：无处不在的云计算

re:Invent现场直击：无处不在的云计算

2012年&#xff0c;第一届亚马逊云科技re:Invent全球大会拉开帷幕的时候&#xff0c;许多人还不知道云计算为何物。2022年&#xff0c;第十一届亚马逊云科技re:Invent全球大会召开的时候&#xff0c;人们发现云计算已经是无处不在。云计算从遥不可及到无处不在美国当地时间2022…
阅读更多...
Clock and Jitter

Clock and Jitter

1、Jitter定义 定义1&#xff08;SONET规范&#xff09;&#xff1a;抖动可以定义为数字信号在重要时点上偏离理想时间位置的短期变化。 2、Total Jitter表征方式 2.1、周期抖动&#xff08;Period Jitter&#xff09;&#xff0c;与理想时钟无关&#xff0c;不累积 Period …
阅读更多...
Qt之QPropertyAnimation移动动画

Qt之QPropertyAnimation移动动画

#include "cpropertyanimationtest.h" #include "ui_cpropertyanimationtest.h" #include<QPropertyAnimation> CPropertyAnimationTest::CPropertyAnimationTest(QWidget *parent) :QWidget(parent),ui
阅读更多...
Mybatis练习(按值单条件查询)

Mybatis练习(按值单条件查询)

Mybatis练习 安装MybatisX 接下来我们就使用Mybatis完成品牌数据的增删改查操作。以下是我们要完成功能列表&#xff1a; 查询 查询所有数据查询详情条件查询 添加修改 修改全部字段修改动态字段 删除 删除一个批量删除 创建数据库 数据库表&#xff08;tb_brand&#xff09;…
阅读更多...
腾讯云服务器CVM和轻量应用服务器区别全方位对比

腾讯云服务器CVM和轻量应用服务器区别全方位对比

腾讯云轻量服务器和云服务器有什么区别&#xff1f;轻量应用服务器和云服务器CVM哪个更好&#xff1f;抛开价格及使用门槛&#xff0c;云服务器CVM更好&#xff1b;从性价比及易用性角度考虑&#xff0c;轻量应用服务器更好&#xff0c;轻量服务器性价比高&#xff0c;这个配置…
阅读更多...
【Python】批量提取图片经纬度并写入csv文件

【Python】批量提取图片经纬度并写入csv文件

需求 无人机图片中往往包含经纬度信息&#xff0c;需要一个脚本批量将文件夹中包含经纬度信息的图片提取出来&#xff0c;保存成csv文件。 经纬度格式解读 默认情况下&#xff0c;图片采用的WGS84经纬度&#xff0c;默认格式采用的是度分秒格式&#xff0c;另一种格式是十进…
阅读更多...
【数据结构】二叉树的基本操作与遍历（C语言）

【数据结构】二叉树的基本操作与遍历（C语言）

目录 定义 满二叉树 完全二叉树 性质 应用 计算二叉树结点个数 计算叶子结点的个数 第 k 层结点的个数 查找值为x的节点 遍历 前序遍历 中序遍历 后序遍历 层序遍历 判断是否为完全二叉树 定义 &#x1f984;二叉树是由树发展过来的&#xff0c;即度最大为2的树&…
阅读更多...
stm32 笔记 PWM及HAL库应用

stm32 笔记 PWM及HAL库应用

stm32 PWM原理 STM32 使用一个定时器作为 PWM 输出&#xff0c;在上图中&#xff0c;ARR 即为重装载值。在计数器的值大于CRRx的值并且小于 ARR 之间&#xff0c;即区分高低电平。输出在图中分别有 ① 和 ② 两种情况. 分别为&#xff1a; ①CRR 和 ARR 区间为低电平。 ②CR…
阅读更多...
【pen200-lab】10.11.1.222

【pen200-lab】10.11.1.222

pen200-lab 学习笔记 【pen200-lab】10.11.1.222 &#x1f525;系列专栏&#xff1a;pen200-lab &#x1f389;欢迎关注&#x1f50e;点赞&#x1f44d;收藏⭐️留言&#x1f4dd; &#x1f4c6;首发时间&#xff1a;&#x1f334;2022年11月27日&#x1f334; &#x1f36d;作…
阅读更多...
Vue框架学习(第十三课)Vuex状态管理中的store和state属性

Vue框架学习(第十三课)Vuex状态管理中的store和state属性

学习官网文档:开始 | Vuex (vuejs.org) 第一部分:查图观色思考为什么&#xff1f;下面的一张图中的数据如何实现组件与组件之间的数据共享呢&#xff1f; 如何去实现下面的方案呢能让数据得到共享 这一张图告诉你们答案 这样如何实现组件与组件之间的通信呀 Vuex五个核心的基本…
阅读更多...
FANUC机器人程序设计

FANUC机器人程序设计

一&#xff0e;注意事项 1.FANUC机器人所有者、操作者必须对自己的安全负责。FANUC不对机器使用的安全问题负责。FANUC提醒用户在使用FANUC机器人时必须使用安全设备&#xff0c;必须遵守安全条款。 2.FANUC机器人程序的设计者、机器人系统的设计和调试者、安装者必须熟悉FAN…
阅读更多...
408 考研《操作系统》第一章第一节：操作系统的概念和特征

408 考研《操作系统》第一章第一节：操作系统的概念和特征

文章目录教程&#xff1a;1. 操作系统的概念、功能和目标1.1 大家熟悉的操作系统1.2 操作系统的概念1.3 操作系统的功能和目标1.3.1 操作系统的功能和目标——作为系统资源的管理者1.3.2 操作系统的功能和目标——作为用户和计算机硬件之间的接口1.3.3 操作系统的功能和目标——…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023