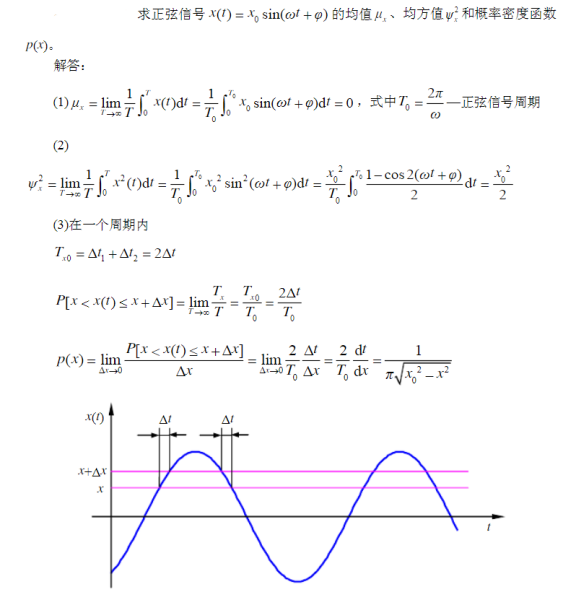
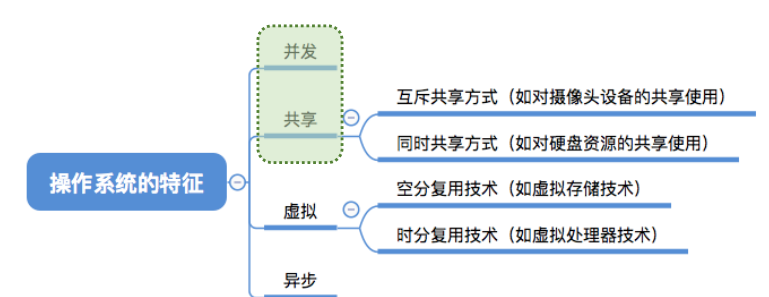
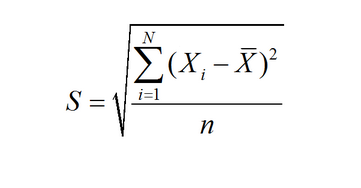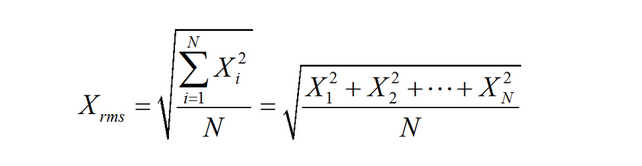1、Jitter定义
定义1(SONET规范):抖动可以定义为数字信号在重要时点上偏离理想时间位置的短期变化。
2、Total Jitter表征方式
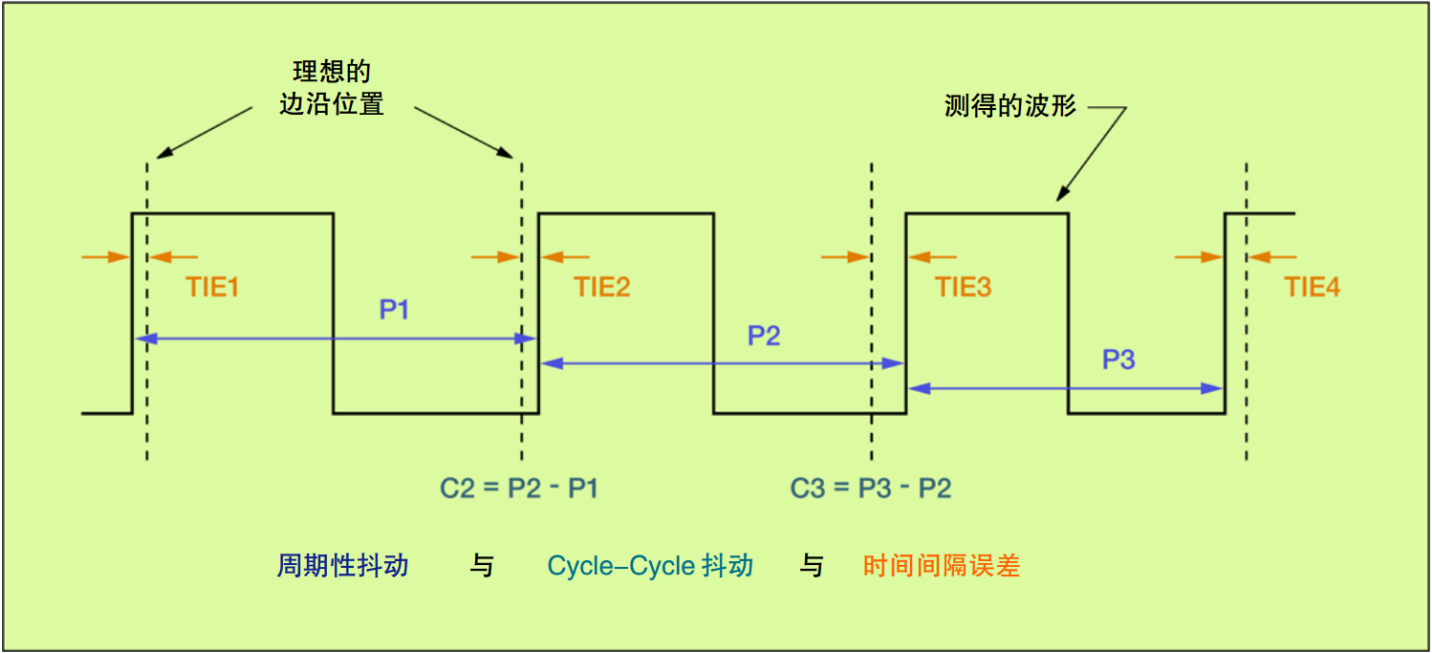
2.1、周期抖动(Period Jitter),与理想时钟无关,不累积
Period jitter is defined as the maximum deviation of any clock period from its mean clock period(替代ideal clock period).
Period jitter is typically specified over a set number of clock cycles. Jedec Specification, JESD65B, suggests, measuring jitter over 10,000 cycles when the clock is in a range of 10 to 100 MHz. However, if clock cycles are not specified, it is recommended to measure period jitter over 100,000 cycles to better represent jitter over an “infinite” time span.
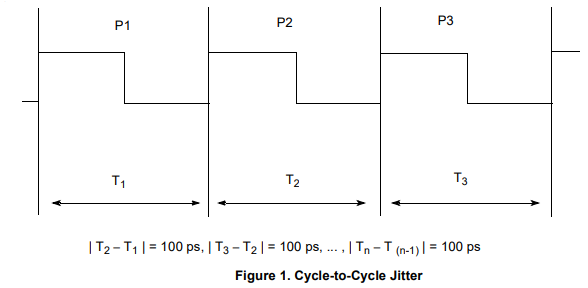
测量项目P1、P2和P3表明的周期性抖动用来测量波形中每个时钟周期的时间。这是可以执行的最简单、最直接的测量。通过调节示波器,并对无穷大余辉设置显示结果,可以显示略长于一个完整时钟周期的周期,进而可以估计峰到峰值。如果示波器在第一个边沿上触发(中间电平触发),可以在第二个边沿上查看周期性抖动,如下图所示。
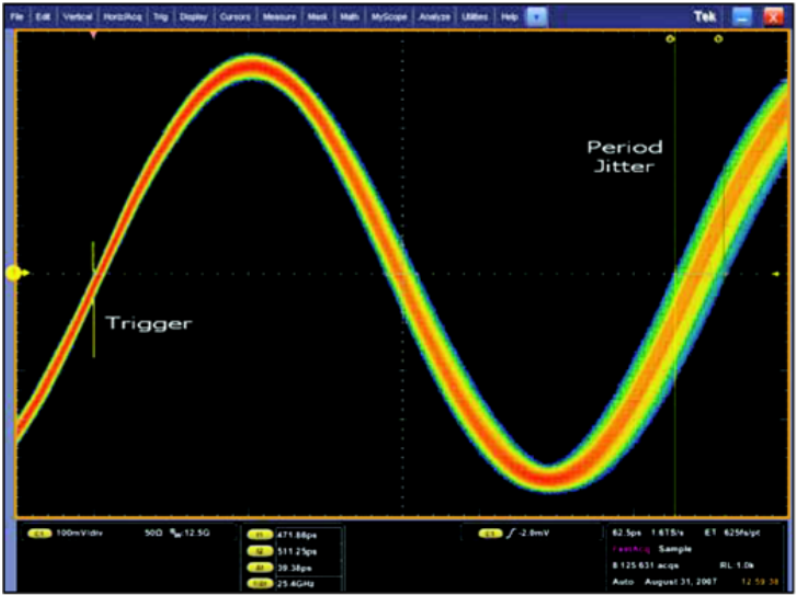
测量实时波形中每个时钟和数据的周期的宽度。这是最早最直接的一种测量抖动的方式。这一指标说明了时钟信号每个周期的变化。
2.1.1、Long term period jitter(K-Cycle jitter or K-Period Jitter)
测量由参考点滞后相当数量K个Cycle(一般K=500~1000)后时钟的抖动值。该抖动参数也是时钟稳定性的一个重要指标。
Period Jitter也就是K=1的Long term period jitter。
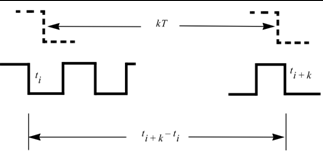
2.2、相邻周期抖动(Cycle-Cycle Jitter),与理想时钟无关,不累积,属于short-term jitter
测量任意两个相邻时钟或数据的周期宽度的变动有多大,通过对周期抖动应用一阶差分运算,可以得到周期间抖动。这个指标在分析锁相环性质的时候具有明显的意义。
2.3、时间间隔误差(Time Interval Error,TIE),与理想时钟有关,且累积
测量时钟或数据的每个活动边沿与其理想位置有多大偏差,它使用参考时钟或时钟恢复提供理想的边沿。TIE在通信系统中特别重要,因为它说明了周期抖动在各个时期的累计效应。
2.4、三者关系
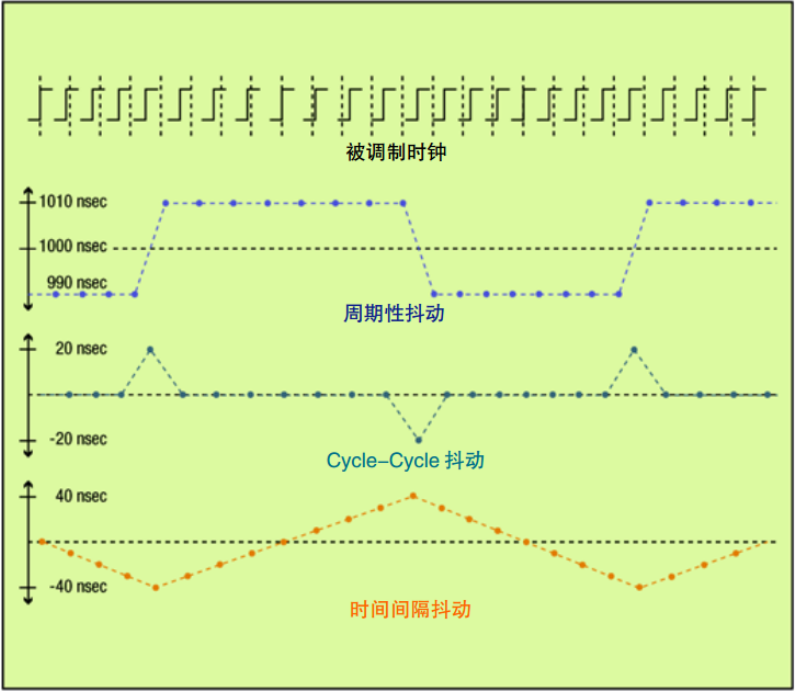
备注:上面的图片关于Period Jitter是错误的,显示的是单纯的Period,而不是Period Jitter。

例:某1MHz时钟(1000ns),测得的周期分别为990、990、990、990、1010、1010、1010、1010…
| Period | 990 | 990 | 990 | 990 | 1010 | 1010 | 1010 | 1010 | 1010 | 1010 | 1010 | 1010 | 990 |
| Period Jitter | -10 | -10 | -10 | -10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | -10 |
| Cycle-Cycle Jitter | NA | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -20 |
| TIE Jitter | -10 | -20 | -30 | -40 | -30 | -20 | -10 | 0 | 10 | 20 | 30 | 40 | 30 |
3、Jitter来源
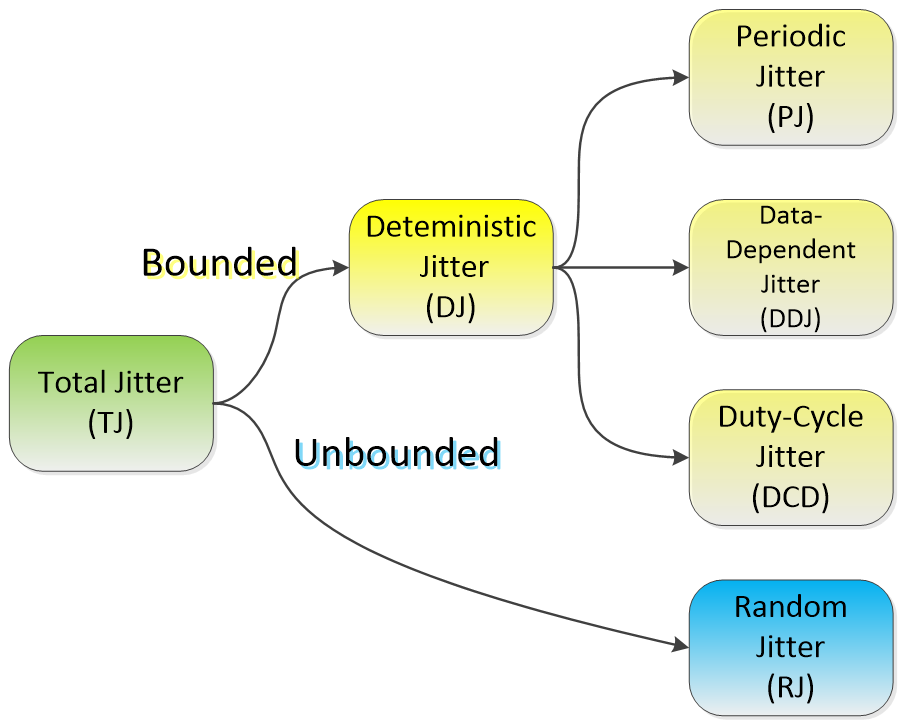
其中,
DCD是Duty-Cycle Distortion;
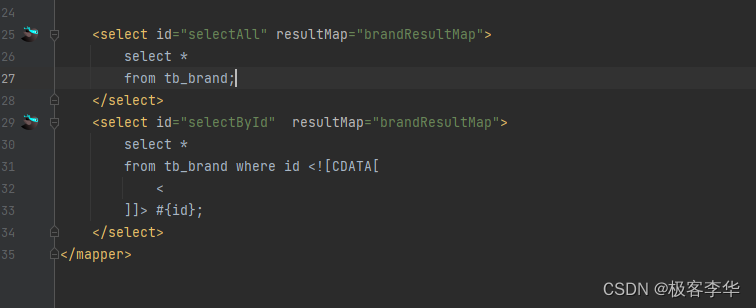
DDJ也有称作Pattern-Dependent Jitter,或ISI。
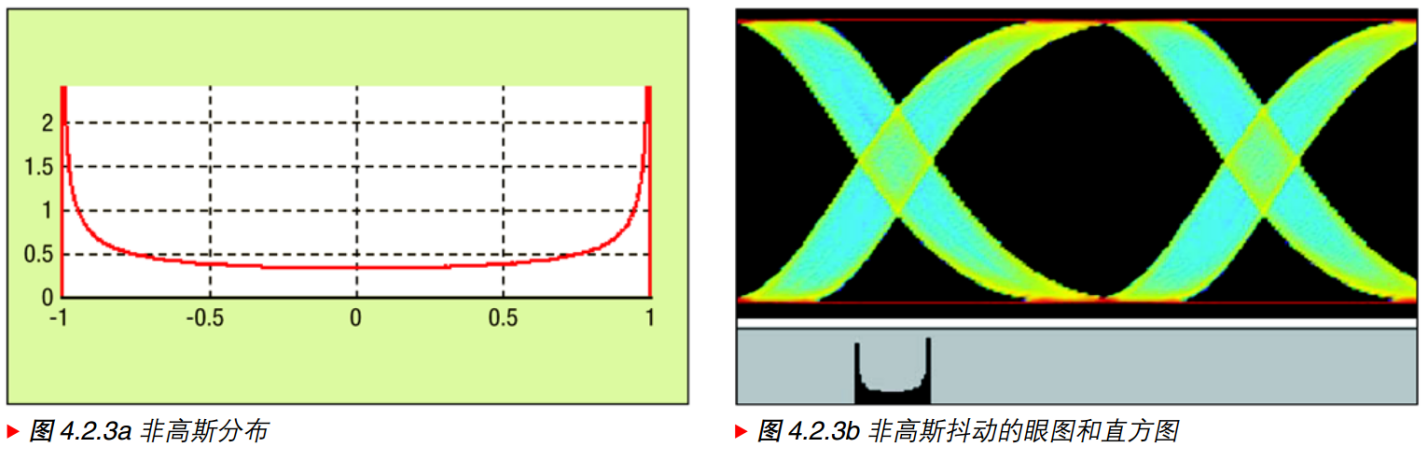
确定性抖动是非高斯分布的,且有界(Bounded)的。

3.1、随机性抖动(Random Jitter):高斯分布

3.2、周期性抖动(Periodic Jitter):正弦函数概率密度,不同于Period Jitter
3.3、数据相关抖动(DDJ):多个独立分布(至少两个)
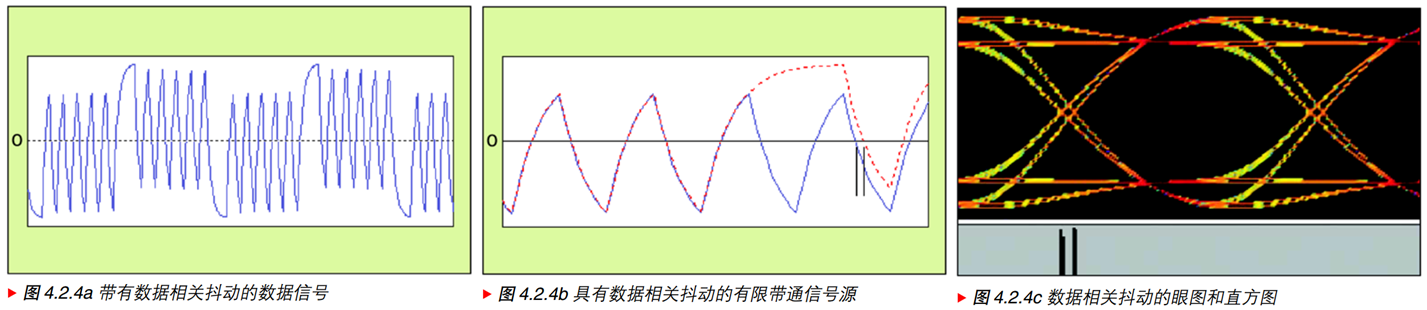
图中PDF是与随机抖动卷积之后的结果,原本应该是两条竖线。
3.4、占空比相关抖动(DCD):两个独立分布

图中PDF是与随机抖动卷积之后的结果,原本应该是两条竖线。
4、Peak to Peak和STD
4.1、Standard deviation is same as RMS(Root Mmean Square),Why?
当平均值时,两者相等,而对于随机抖动而言,平均值可以认为等于0。
5、附录
5.1、正弦函数概率密度函数