图像识别是计算机视觉最常用的任务之一,几乎所有的有关图像识别的教程都会将MNIST数据集作为入门数据集,因为MNIST数据集是图像识别问题中难度最小、特征差异较为明显的数据集,非常适合作为图像识别入门者的学习案例。本案例使用MNIST数据集,基于LeNet-5网络实现手写数字的识别任务。
本节中的所有代码在Ubuntu 20.04+Python 3.8.10+TensorFlow 2.9.1+Keras 2.9.0环境中实测通过,具体代码详见LeNet_MNIST.py文件,读者可以直接使用。
MNIST的全称是Modified National Institute of Standards and Technology,其中美国国家标准与技术研究所(NIST)是美国商务部下属的一个研究机构,MNIST数据集是这个机构通过收集不同人的手写数字进行整理得到的。
MNIST数据集由训练集(Training Set)和测试集(Test Set)两部分构成,其中训练集有60 000幅手写数字图片和标签,由250个不同的人手写的数字构成,测试集有10 000幅手写数字图片和标签。这些手写数字图片的内容为0~9这10个数字,都是28×28像素大小的灰度图,灰度图中每个像素都是一个0~255的灰度值。
MNIST数据集自1998年起,被广泛地应用于机器学习和深度学习领域,用来测试算法的效果,如果一个图像识别算法在MNIST数据集上效果差,那么在其他数据集上的表现效果也不会很好。
MNIST数据集可以通过MNIST官网下载。当然,目前许多深度学习框架已经内置了MNIST数据集,并且有相关的函数直接读取并划分数据集。如图6.29所示为MNIST数据集中部分手写数字的可视化图像展示。

图6.29 MNIST数据集中部分手写数字的可视化图像能展示
本案例使用LeNet-5网络实现对上述MNIST数据集图片中数字0~9的识别。
1. 数据加载
MNIST数据集已经被集成在TensorFlow Keras框架中,可以使用Keras模块的mnist.load_data()函数直接加载,由于MNIST数据集由TensorFlow提前规划好,该函数会分别返回训练集数据和标签(train_images,train_labels)、测试集数据和标签(test_images,test_labels)。
其中,train_images是一个60 000×28×28的三维矩阵,第一维60 000代表样本量,其余两维为图片长×宽的像素矩阵,因为只是灰度图,所以没有通道数。
其中,train_labels是一个大小为60 000的一维数组,分别表示这60 000幅图片是数字0~9中的哪一个。
2. 数据预处理
数据加载之后需要进行必要的预处理,因为此时的train_images、train_labels、test_images、test_labels都不满足LeNet-5对TensorFlow的数据要求。
- LeNet-5的每个输入数据应为32×32×1的三维数据,train_images和test_images的每个样本数据没有通道数,需要扩展一个通道数,可以调用reshape()函数扩展到需要的维度。
- train_images和test_images每个像素灰度值是一个0~255的整数,为了使模型的优化算法更容易收敛,需要将其调整为0~1的浮点数。
- 本案例是一个多分类识别问题,LeNet-5网络要求对应的分类标签使用On-Hot编码形式,需要将train_labels和test_labels从整数调整为One-Hot数组,可以调用内置于Keras的to_categorical()函数实现One-Hot编码。
3. 代码示例
【例6.12】MNIST数据加载和预处理。
import tensorflow as tf
from keras.utils import np_utils
#加载和预处理数据
def load_images_data():
#加载图像和标签数据
(train_images,train_labels),(test_images,test_labels) = tf.keras.datasets.mnist.load_data()
print("train_images:", train_images.shape)
print("train_labels:", train_labels.shape)
print("test_images:", test_images.shape)
print("test_labels:", test_labels.shape)
#预处理数据
N0 = train_images.shape[0]
N1 = test_images.shape[0]
print(N0,N1)
train_images = train_images.reshape(N0,28,28,1)
train_images = train_images.astype('float32') / 255
train_labels = np_utils.to_categorical(train_labels)
test_images = test_images.reshape(N1,28,28,1)
test_images = test_images.astype('float32') / 255
test_labels = np_utils.to_categorical(test_labels)
return train_images,train_labels,test_images,test_labels
输出结果如图6.30所示。

图6.30 输出结果
完成了数据加载和预处理工作,接下来用代码实现LeNet-5模型的网络结构搭建。
1. 网络参数设计
参考上一节对LeNet-5网络结构的介绍,本案例对各层的参数设置如下:
- 输入层:一幅28×28的灰度图像,只有一个通道,输入矩阵大小为28×28×1。
- 第一个卷积层:使用6个5×5×1的卷积核进行same卷积。由于输入的是灰度图,因此卷积核的深度是1;又由于使用same卷积,因此卷积后的输出矩阵维度为28×28×6(因为用了6个卷积核)。
- 第一个池化层:使用6个2×2大小的矩阵进行最大值池化处理,输出结果矩阵为14×14×6。
- 第二个卷积层:使用16个5×5×6的卷积核进行valid卷积,输出结果矩阵为10×10×6。
- 第二个池化层:同样使用6个2×2的最大值池化,输出矩阵的维度为5×5×16。
- 全连接层:将上一个池化层输出的矩阵拉直成一维向量,向量大小为5×5×16=400,第一个隐藏层使用120个神经元,第二个隐藏层使用84个神经元。
- 输出层:因为网络模型的目的是识别0~9的数字,处理的是一个10分类的问题,所以其输入层有10个神经元。
【例6.13】网络参数和训练参数的定义。
#输入层大小
INPUT_SHAPE = (28,28,1)
#第一个卷积层的卷积核的大小和数量
CONV1_SIZE = 5
CONV1_NUM = 6
#第二个卷积层的卷积核的大小和数量
CONV2_SIZE = 5
CONV2_NUM = 16
#池化层窗口大小
POOL_SIZE = 2
#全连接层节点个数
FC1_SIZE = 120
FC2_SIZE = 84
#输出个数
OUT_SIZE = 10
#训练参数
EPOCH_SIZE = 20
BATCH_SIZE = 200
2. 构建LeNet-5网络模型
LeNet-5是一个卷积神经网络,包含一些卷积、池化、全连接的简单线性堆积。我们知道多个线性层堆叠实现的仍然是线性运算,添加层数并不会扩展假设空间(从输入数据到输出数据的所有可能的线性变换集合),因此还需要添加非线性的激活函数。
两个卷积层conv1和conv2是图像与卷积核卷积后得到的特征图,激活函数可以理解为再对卷积结果进行一个范围限制,ReLU是最常用的激活函数。
对于最后的输出层,我们需要从输出的10个特征维度中选取最大的那一个,为了达到这个目的,需要把它们转换为一个和为1的概率形式,以方便后续使用相应的损失函数,来评估模型预测结果的优劣以及与目标结果(标签)的差异,因此可以选择使用Softmax激活函数。
有了前面设计的网络结构参数,使用TensorFlow和Keras框架的models模块、layer模块,可以非常方便、快速地构建网络。
【例6.14】创建LeNet-5模型。
from keras import models
from keras import layers
#创建LeNet-5网络
def build_LeNet5():
model = models.Sequential()
#第一层:卷积层
model.add(layers.Conv2D(filters=CONV1_NUM,kernel_size=(CONV1_SIZE, CONV1_SIZE),padding="same",activation='relu',input_shape=INPUT_SHAPE,name="layer1-conv1"))
#第二层:最大池化层
model.add(layers.MaxPooling2D(pool_size=(POOL_SIZE,POOL_SIZE), name="layer2-pool"))
#第三层:卷积层
model.add(layers.Conv2D(filters=CONV2_NUM,kernel_size=(CONV2_SIZE, CONV2_SIZE),padding="valid",activation='relu',name="layer3-conv2"))
#第四层:最大池化层
model.add(layers.MaxPooling2D(pool_size=(POOL_SIZE,POOL_SIZE), name="layer4-pool"))
model.add(layers.Flatten(name="layer4-flatten"))
#第五层:全连接层
model.add(layers.Dense(units=FC1_SIZE,activation='relu',name="layer5-fc1"))
model.add(layers.Dense(units=FC2_SIZE,activation='relu',name="layer5-fc2"))
#第六层:Softmax输出层
model.add(layers.Dense(units=OUT_SIZE,activation='softmax',name="layer6-fc"))
return model
创建完成后,可以使用model.summary()函数输出模型的概要内容,输出结果如图6.31所示。

图6.31 输出结果
上述概要中列出了各层中需要训练的参数个数,从中可以发现卷积层和池化层相较于全连接层来说,极大地减少了参数的数量。读者还可以自行画出上述网络并手工计算和理解所需的参数。
1. 模型编译
模型编译通过model.compile()函数实现。需要告诉TensorFlow这是一个多分类问题,它的损失函数(用于计算预测值与目标值之间的差距)使用categorical_crossentropy(交叉熵损失函数),优化器(用于指定梯度下降更新参数的具体方法)使用Adam(Adam是目前深度学习中图像分类相关任务中最常用的优化器算法,是一种优秀的自适应学习率的方法),需要监控预测精度以评价模型性能指标,因此评价指标(Metrics)(用于评价模型在训练和测试时的性能指标)设置为Accuracy(精度)。
2. 模型训练
模型训练(拟合)通过model.fit()函数实现。需要告诉TensorFlow使用的训练数据x和对应标签y、测试(验证)的数据和其对应标签validation_data,指定进行循环的次数epochs以及批量处理的批量数据大小batch_size。设置批量处理的意义在于,由于深度学习网络模型在单个数据上并不是特别稳定,为了保证训练出来的模型稳定,在数据上会进行批量归一化处理,每次选取一批数据进行归一化,弱化噪声数据对模型训练的影响。
3. 代码示例
【例6.15】编译和训练模型。
#模型训练
def train_LeNet5(model,train_data,train_labels,test_data,test_labels):
model.compile(loss='categorical_crossentropy',optimizer='adam', metrics=['accuracy'])
history = model.fit(x=train_data,y=train_labels,epochs=EPOCH_SIZE, batch_size=BATCH_SIZE,validation_data=[test_data,test_labels])
return history
输出结果如图6.32所示。
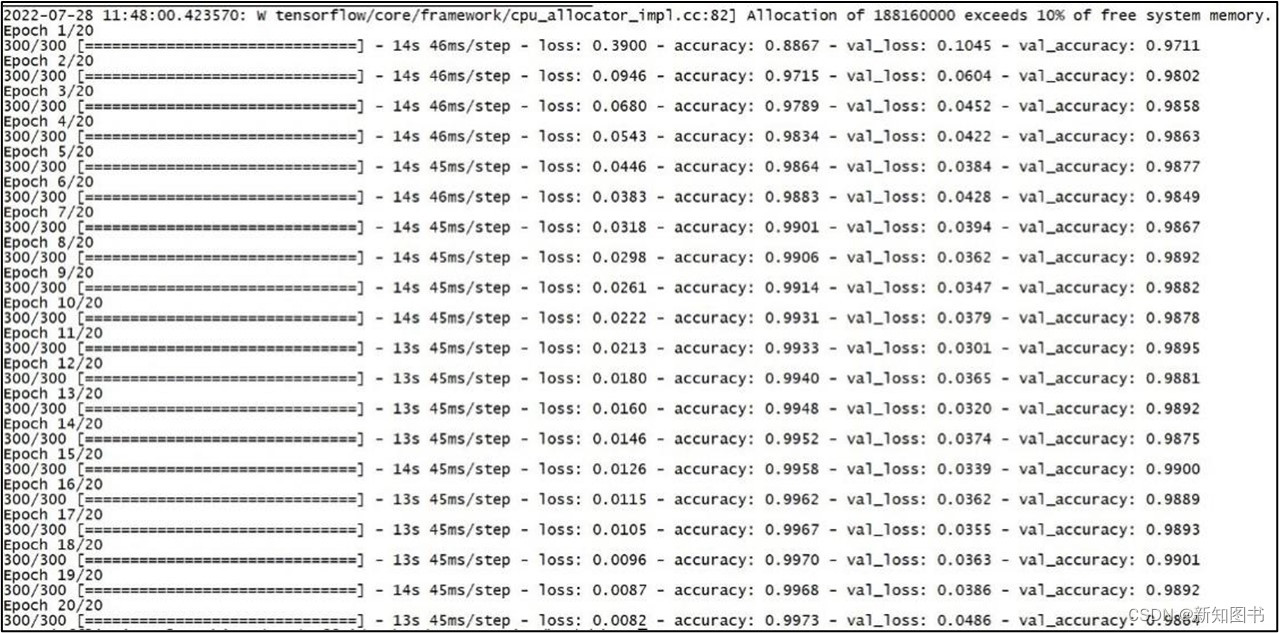
图6.32 模型训练
上述结果实时显示了每轮epoch执行时训练数据和验证数据的损失值(Loss)和预测精度(Accuracy),这些数据保存在fit()返回的history数据中,可以通过如下代码直观地画出其曲线图并将图形保存为文件。
【例6.16】图形化显示训练结果。
from matplotlib import pyplot as plt
#绘制loss和accuracy
def draw_history(history):
loss = history.history['loss']
accuracy = history.history['accuracy']
val_loss = history.history['val_loss']
val_accuracy = history.history['val_accuracy']
epochs = range(1, len(loss) + 1)
#draw loss with epoch
plt.subplot(2,2,1)
plt.plot(epochs,loss,'bo')
plt.title("Training loss")
plt.xlabel('Epoch')
plt.ylabel('Loss')
#draw accuracy with epoch
plt.subplot(2,2,2)
plt.plot(epochs,accuracy,'bo')
plt.title("Training accuracy")
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
#draw val_loss with epoch
plt.subplot(2,2,3)
plt.plot(epochs,val_loss,'bo')
plt.title("Validate loss")
plt.xlabel('Epoch')
plt.ylabel('Loss')
#draw val_accuracy with epoch
plt.subplot(2,2,4)
plt.plot(epochs,val_accuracy,'bo')
plt.title("Validate accuracy")
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.tight_layout()
plt.show()
#save to file
plt.savefig(fname="LetNet5-history.png",format='png')
执行结果如图6.33所示。
从执行结果可以看出,该模型经过训练(拟合)后,模型的识别精度(Accuracy)可以达到99%。同时可以从曲线上大体看出,增加epoch循环次数时,随着在训练数据集上的精度(Training accuracy)不断提高,在验证数据集上的精度(Validate Accuracy)并没有不断提高,所以Epoch和batch_size会对模型的性能产生一定的影响,需要反复尝试选择合理的数值。
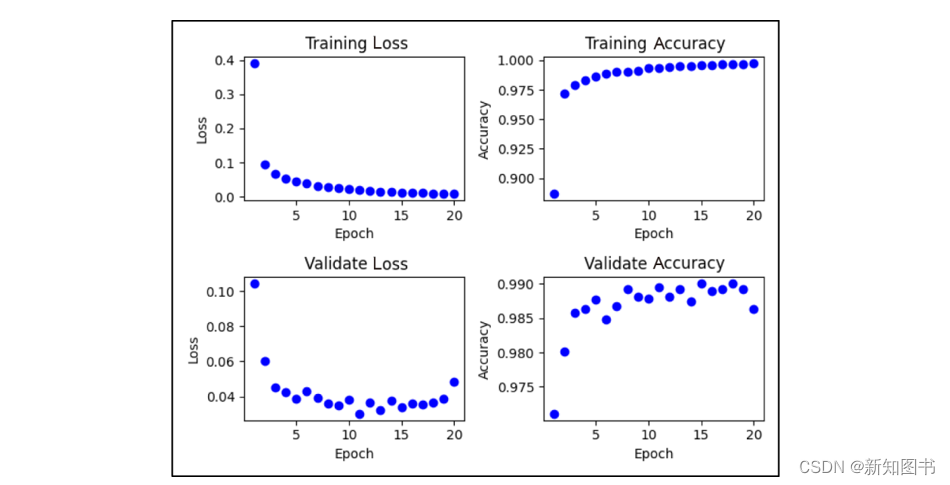
图6.33 模型训练结果
本文节选自《Python深度学习原理、算法与案例》,内容发布获得作者和出版社授权。