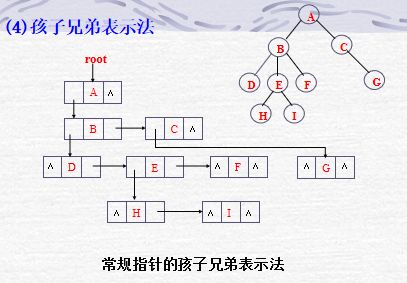
在我们之前已经了解的堆这样的完全二叉树的实现,也对树型结构有了一些了解,那么今天我们来看看二叉树的一些性质。
因为二叉树是一种每个节点至多只有两个子树(即二叉树的每个节点的度不大于2),并且二叉树的子树有左右之分,其次序不能任意颠倒,因此它的结构也是比较独特的。
目录
1.二叉树的结构定义
2.节点构造
3.节点生成树
3.二叉树的遍历方式
先序遍历:
中序遍历:
后序遍历
层次遍历:
4.求树的所有节点个数
5.求叶子节点个数
6.求二叉树树深度
7.二叉树第K层节点个数
8.返回值为x的节点
1.二叉树的结构定义
二叉树是一种每个节点至多只有两个子树(即二叉树的每个节点的度不大于2),并且二叉树的子树有左右之分,其次序不能任意颠倒。
//定义树的节点
typedef int DATAtype;
typedef struct TreeNode
{
DATAtype data;
struct TreeNode* leftchild;
struct TreeNode* rightchild;
}BTnode;2.节点构造
简单的节点构造,如同链表的结点,不同的是这里有两个节点表示左孩子与右孩子。
//构造树的节点
BTnode* CreateNode(DATAtype x)
{
BTnode* newnode = (BTnode*)malloc(sizeof(BTnode));
if (newnode == NULL)
{
perror("malloc fali");
return NULL;
}
newnode->data = x;
newnode->leftchild = NULL;
newnode->rightchild = NULL;
return newnode;
}3.节点生成树
我们是通过链接节点之间形成树的逻辑关系,这里的树如图:
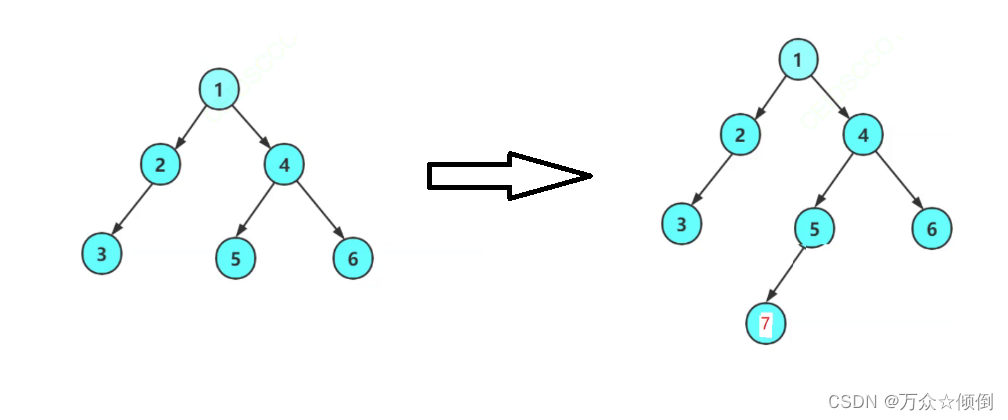
先链接了六个节点,之后又添加了一个节点
//利用节点生成一个树
BTnode* TreeCreat()
{
BTnode* node1=CreateNode(1);
BTnode* node2=CreateNode(2);
BTnode* node3=CreateNode(3);
BTnode* node4=CreateNode(4);
BTnode* node5=CreateNode(5);
BTnode* node6=CreateNode(6);
BTnode* node7 = CreateNode(6);
//建立连接关系
node1->leftchild = node2;
node1->rightchild = node4;
node2->leftchild = node3;
node4->leftchild = node5;
node4->rightchild = node6;
node6->leftchild = node7;
//返回根
return node1;
}3.二叉树的遍历方式
二叉树的遍历方式主要有四种,分别是先序遍历、中序遍历、后序遍历和层次遍历。123
先序遍历:
先访问根节点,再访问左子树,最后访问右子树。
//前序遍历
void Preverorder(BTnode*root)
{
//根 左子树 右子树
if (root == NULL)
{
return;
}
printf("%d ", root->data);
Preverorder(root->leftchild);
Preverorder(root->rightchild);
}
中序遍历:
先访问左子树,再访问根节点,最后访问右子树。
void Inorder(BTnode* root)
{
// 左子树 根 右子树
if (root == NULL)
{
return;
}
Preverorder(root->leftchild);
printf("%d ", root->data);
Preverorder(root->rightchild);
}
后序遍历
:先访问左子树,再访问右子树,最后访问根节点。
void Postorder(BTnode* root)
{
// 左子树 右子树 根
if (root == NULL)
{
return;
}
Preverorder(root->leftchild);
Preverorder(root->rightchild);
printf("%d ", root->data);
}
层次遍历:
按照从上到下、从左到右的顺序依次访问每个节点。
层序遍历我们使用队列实现,思路:先进先出,上一层出队时带下一层节点入队。
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include"queue.h"
#define CRT_SECURE_NO_WARNINGS 1
//定义树的节点
typedef int DATAtype;
typedef struct TreeNode
{
DATAtype data;
struct TreeNode* leftchild;
struct TreeNode* rightchild;
}BTnode;
//构造树的节点
BTnode* CreateNode(DATAtype x)
{
BTnode* newnode = (BTnode*)malloc(sizeof(BTnode));
if (newnode == NULL)
{
perror("malloc fali");
return NULL;
}
newnode->data = x;
newnode->leftchild = NULL;
newnode->rightchild = NULL;
return newnode;
}
//利用节点生成一个树
BTnode* TreeCreat()
{
BTnode* node1=CreateNode(1);
BTnode* node2=CreateNode(2);
BTnode* node3=CreateNode(3);
BTnode* node4=CreateNode(4);
BTnode* node5=CreateNode(5);
BTnode* node6=CreateNode(6);
BTnode* node7 = CreateNode(6);
//建立连接关系
node1->leftchild = node2;
node1->rightchild = node4;
node2->leftchild = node3;
node4->leftchild = node5;
node4->rightchild = node6;
node6->leftchild = node7;
//返回根
return node1;
}层序遍历:
//层序遍历
void leverorder(BTnode* root)
{
LTnode p;
Queueinit(&p);
Queuedestroy(&p);
//先入根节点
if (root)
{
LTpush(&p, root);
}
while (!LTempety(&p))
{
//队中数据全是树节点指针型
BTnode* front = LTfront(&p);
LTpop(&p);//出队头
printf("%d", front->data);
//判断孩子节点
if (front->leftchild)
{
LTpush(&p, front->leftchild);
}
if (front->rightchild)
{
LTpush(&p, front->rightchild);
}
}
printf("\n");
}4.求树的所有节点个数
这里有两种方法,除了定义全局变量利用计数的方法来计算树的节点个数,但还需注意全局变量使用后需置零,其次我们也是利用递归的返回值累加计算出节点个数。
//求树的所有节点个数
int size = 0;
int Binarytreesize(BTnode* root)
{
/*分治思想 从左子树到右子树再到根*/
if (root == NULL)
{
return 0;
}
return (1 + Binarytreesize(root->leftchild) + Binarytreesize(root->rightchild));
/*if (root)
{
size++;
Binarytreesize(root->leftchild);
Binarytreesize(root->rightchild);
}
return size;*/
}5.求叶子节点个数
寻找递归条件,叶子节点没有左右孩子,否则就不返回一,符合条件的返回一相加。注意递归中返回值的设定。
//求叶子节点个数
int BTreeleavessize(BTnode* root)
{
//自己的左子树与左右子树为空
if (root == NULL)
{
return 0;
}
if (root->leftchild == NULL && root->rightchild == NULL)
{
return 1;
}
else
{
return BTreeleavessize(root->leftchild) + BTreeleavessize(root->rightchild);
}
}6.求二叉树树深度
分治思想,两边同时遍历,每有一层加一,左孩子层数与右孩子层数中较大的那个就是深度。
//求二叉树的深度
int BTreeheight(BTnode* root)
{
//左右同时遍历,选最大的哪一个
if (root == NULL)
{
return 0;
}
//这里注意用变量保存一下左 右子树的数目
int left = BTreeheight(root->leftchild) + 1;
int right= BTreeheight(root->rightchild) + 1;
if (left > right)
{
return left;
}
else
{
return right;
}
}7.二叉树第K层节点个数
这里的递归主要是找的第k层,利用k==1作为递归返回条件。
//二叉树第k层结点的个数
int BTree_knumber(BTnode* root,int k)
{
//分情况讨论
if (root == NULL)
{
return 0;
}
if (k==1)
{
return 1;
}
return BTree_knumber(root->leftchild, k - 1) +
BTree_knumber(root->rightchild, k - 1);
}8.返回值为x的节点
这里的难度在与返回值,我们知道在递归里面函数返回值不能直接返回,我们需要判断,对于返回值是需要我们好好检查的,在这里,我们从根,左孩子,右孩子的顺序逐个判断,对于左右孩子并保存返回值,来确定是当前节点。
//返回为x的树节点
BTnode* BTreenode(BTnode* root, DATAtype x)
{
if (root == NULL)
{
return NULL;
}
if (root->data == x)
{
return root;
}
BTnode* left = BTreenode(root->leftchild,x);
if (left->data==x)
{
return left;
}
BTnode* right = BTreenode(root->rightchild,x);
if (right->data==x)
{
return right;
}
return NULL;
}一些测试用例:
int main()
{
BTnode* root = TreeCreat();
/*Preverorder(root);
printf("\n");
Inorder(root);
printf("\n");
Postorder(root);*/
//Binarytreesize(root);
// BTreeleavessize(root);//BTreeheight(root);
int x = BTree_knumber(root, 2);
printf("%d ", BTreenode(root, 2)->data);
//printf("%d", x);
return 0;
}