1．简述列联表的构造与列联表的分布。

答：列联表是将两个以上的变量进行交叉分类的频数分布表。

列联表的分布可以从两个方面看，一个是观察值的分布，又称为条件分布，每个具体的观察值就是条件频数；一个是期望值的分布。

2．用一张报纸、一份杂志或你周围的例子构造一个列联表，说明这个调查中两个分类变量的关系，并提出进行检验的问题。

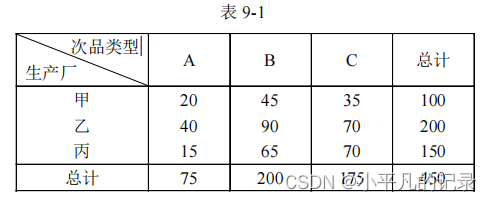
答：对三个生产厂甲、乙、丙提供的学习机的 A、B、C 三种性能进行质量检验，欲了解生产厂家同学习机性能的质量差异是否有关系。抽查了 450 部学习机次品，整理成为如表 9-1 所示的 3×3 列联表。

根据抽查检验的数据表明：次品类型与厂家（即哪一个厂）生产是无关的（即是相互独立的）。

建立假设：H0：次品类型与厂家生产是独立的；H1：次品类型与厂家生产不是独立的。

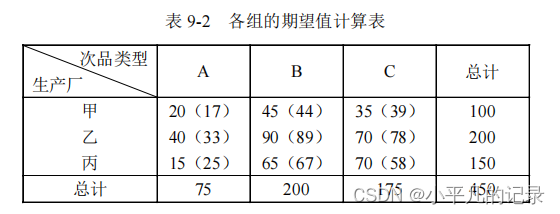
可以计算各组的期望值，如表 9-2 所示（表中括号内的数值为期望值）。

所以$\chi 2＝(20－17{)}^2/17＋(40－33{)}^2/33＋...＋(70－58{)}^2/58＝9.821。$

而自由度等于（R－1）（C－1）＝（3－1）×（3－1）＝4，若以 0.01 的显著性水平进行检验，查 χ^2 分布表得 ${\chi }_{0.01}^2(4)＝13.277$。由于 $χ 2＝9.821＜χ_{0.01}^ 2(4)＝13.277，故接受原假设H0，即次品类型与厂家生产是独立的。

3．说明计算 $\chi 2$ 统计量的步骤。

答：计算 ${\chi }^2$ 统计量的步骤：

（1）用观察值 $f_0$ 减去期望值 $f_e$；

（2）将（$f_0－f_e$）之差平方；

（3）将平方结果（$f_0－f_e$） 2 除以 $f_e$；

（4）将步骤（3）的结果加总，即得：

$${\chi }^2=\sum \frac{(f_0-f_e{)}^2}{f_e}$$

4．简述 φ 系数、c 系数、V 系数的各自特点。

答：（1）φ 相关系数是描述 2×2 列联表数据相关程度最常用的一种相关系数。它的计算公式为：

$$\phi =\sqrt{{\chi }^2/n}$$

式中，

$${\chi }^2=\sum \frac{(f_0-f_e{)}^2}{f_e}$$

出的 φ 系数可以控制在 0～1 这个范围。

（2）列联相关系数又称列联系数，简称 c 系数，主要用于大于 2×2 列联表的情况。c 系数的计算公式为：

$$c=\sqrt{\frac{{\chi }^2}{{\chi }^2+n}}$$

当列联表中的两个变量相互独立时，系数 c＝0，但它不可能大于 1。c 系数的特点是，其可能的最大值依赖于列联表的行数和列数，且随着 R 和C 的增大而增大。

（3）格莱姆（Gramer）提出了 V 系数。V 系数的计算公式为：

$$V=\sqrt{\frac{{\chi }^2}{n\times min[(R-1),(C-1)]}}$$

当两个变量相互独立时，V＝0；当两个变量完全相关时，V＝1。所以 V 的取值在 0～1 之间。如果列联表中有一维为 2，即min[(R-1),(C-1)]＝1，则 V 值就等于 φ 值。

5．构造下列维数的列联表，并给出 ${\chi }^2$检验的自由度。

a．2 行 5 列

b．4 行 6 列

c．3 行 4 列

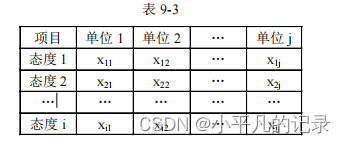
答：i 行 j 列联表，如表 9-3 所示。

而${\chi }^2$检验的自由度＝(行数－1)(列数－1)，所以

a．当 i＝2，j＝5 时，表 9-3 即为 2 行 5 列的列联表，其 χ 2 检验的自由度＝（2－1）×（5－1）＝4；

b．当 i＝4，j＝6 时，表 9-3 即为 4 行 6 列的列联表，其 χ 2 检验的自由度＝（4－1）×（6－1）＝15；

c．当 i＝3，j＝4 时，表 9-3 即为 3 行 4 列的列联表，其 χ 2 检验的自由度＝（3－1）×（4－1）＝6。