Introduction

大语言模型现在已经展示了很好的效果在各种下游任务，如GPT4。但是GPT的数学能力还没有达到最优。

在这篇文章中，作者提出了Goat，通过领域数据微调LLaMA，包含1M指令数据，实现了在基础数学上的Sota水准。

然而在训练期间，作者也遭遇了一些困难，如在较大数值上的乘除法。
为了解决这个难题，作者把数据分为可学习问题与不可学习问题，当遇到与可学习问题，把它分解为多个乘除法。

Method

语言模型

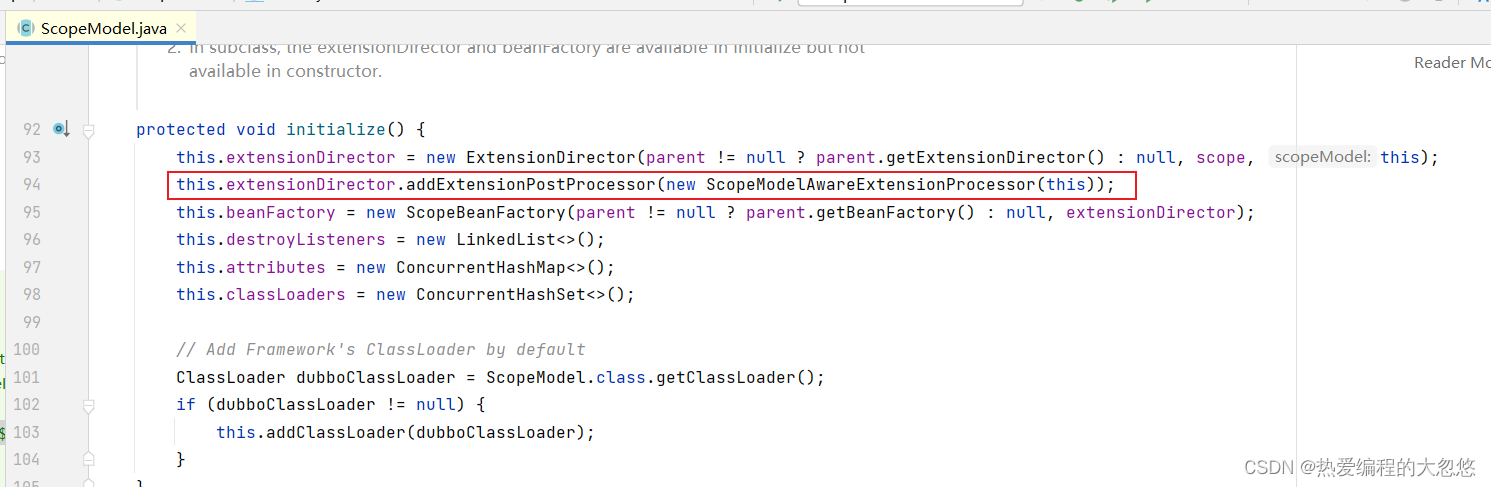
作者认为数学能力表现出了Sota的能力归因于LLaMA的tokenizer，因为它可以把每一个数字分解成一个单独的token，而其他模型则不可以。如下图：

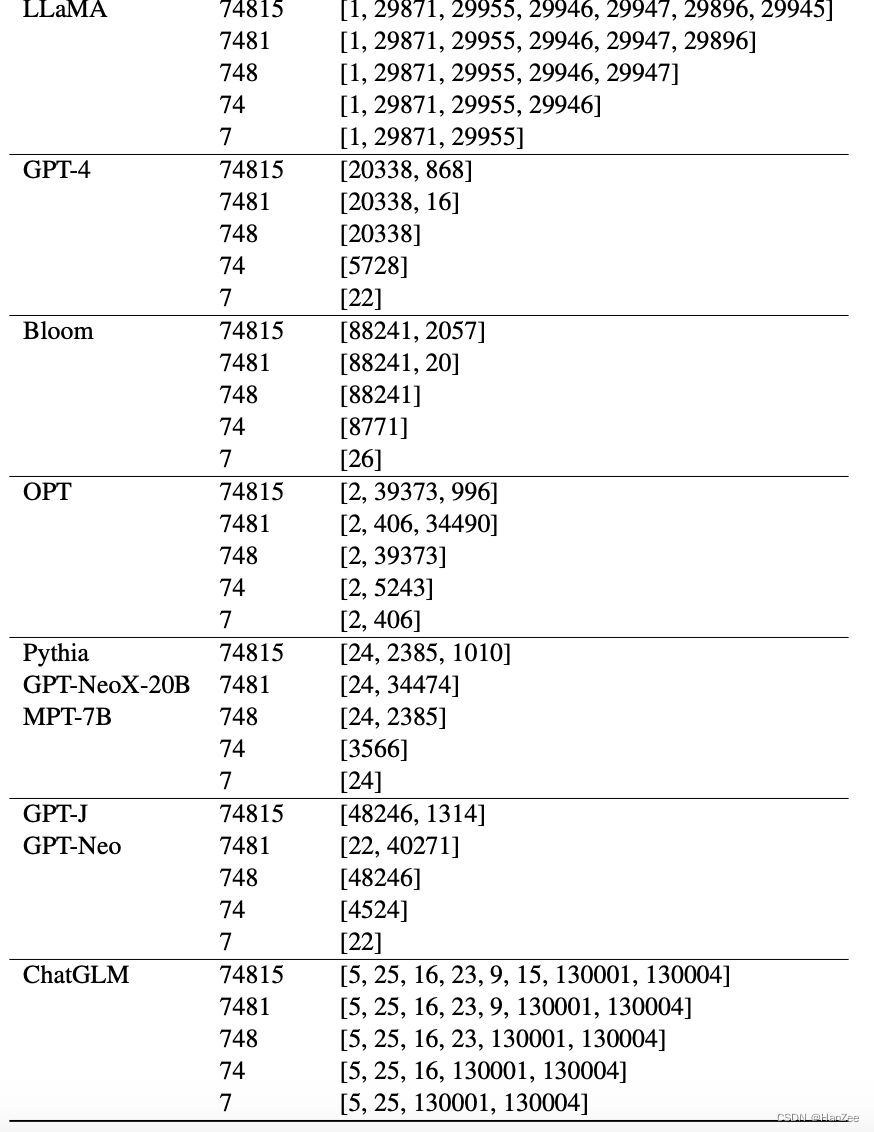
数学问题学习能力

在某个领域任务中，有些任务是可以学习的，有些任务是不能学习的，不可学习的任务可以分解为可学习的CoT任务。

作者通过实验，把数学任务分为这两类。可学习的任务，在一定的训练下就可以实现 高质量的直接输出。
而不可学习的任务，即使拓展再多的数据进行训练，即使是GPT4也不会有很好的结果。
通过Fine-tune成功分类了两类任务，如下图：

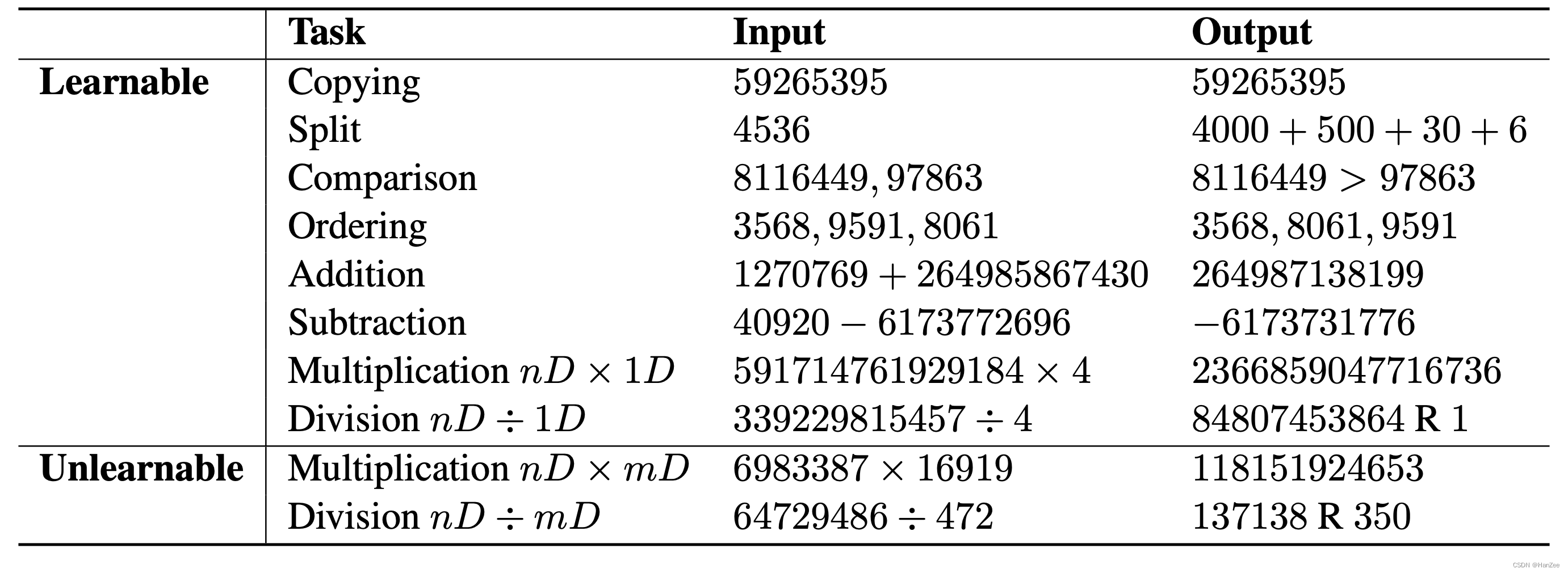
unlearnable 的任务为复杂的乘法与除法，这也符合人类的直觉。

作者也通过实验证明了之前的假设，在其他tokenizer的算法中，采取finetune的方法证明了其他tokenizer效果不好，甚至在LLaMA任务简单的任务效果也不好。

不是所有被划分为unlearnalbe的任务都不可学习，比如两位数✖️两位数的计算，可以通过在10个epoch上过拟合的方式得到90准确度。

相反的，采用之前的提及的分解CoT的方法，仅在1个epoch就可以达到很好的效果。

COT

作者把多位乘法与除法分解，以乘法为例子，把大的数放在左边，分解右面的小一点数（为了CoT长度不超过限制），分解为可学习的乘法，然后相加。

实验

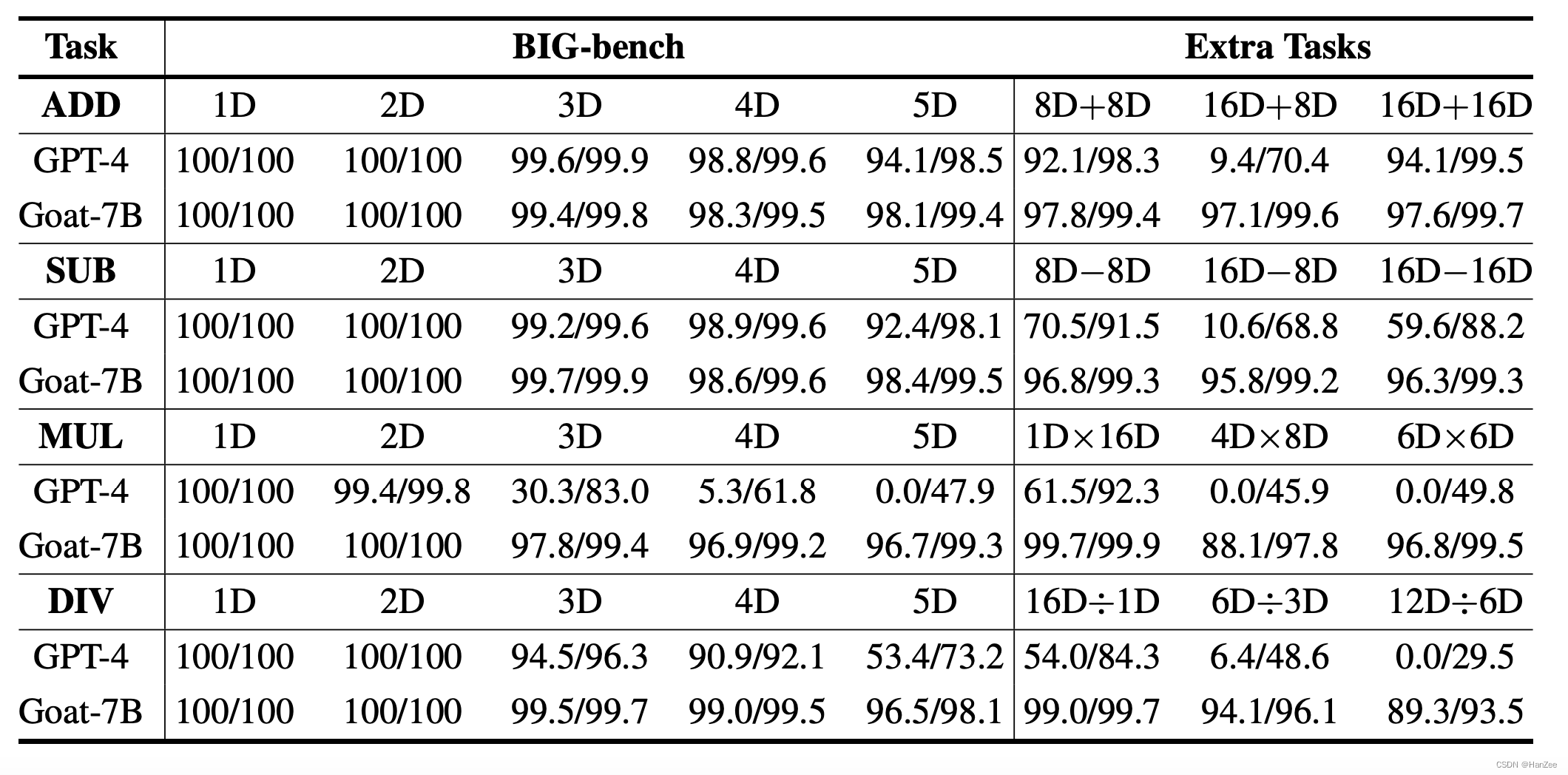
参考

https://arxiv.org/pdf/2305.14201.pdf