6.2 图的遍历

6.2.1 图的遍历——DFS

遍历：把图里面每个顶点都访问一遍而且不能有重复的访问

深度优先搜索(DFS)

当访问完了一个节点所有的灯后，一定原路返回对应着堆栈的出栈入栈的一个行为

深度优先搜索的算法描述

void DFS(Vertex V)//从迷宫的节点出来
{
visited[V] = true;//给每个节点一个变量，true相当于灯亮了，false则是熄灭状态
for(V的每个邻接点W)//视野看得到的灯
if(!visited[W])//检测是否还有没点亮的
DFS(W);//递归调用
}
//类似树的先序遍历
若有N个顶点、E条边，时间复杂度是
用邻接表存储图，有O(N+E)//对每个点访问了一次，每条边也访问了一次
用邻接矩阵存储图，有O(N²)//V对应的每个邻接点W都要访问一遍

6.2.2 图的遍历——BFS

广度优先搜索(Breadth First Search,BFS)

xx

void DFS(Vertex V)//从迷宫的节点出来
{
visited[V] = true;//给每个节点一个变量，true相当于灯亮了，false则是熄灭状态
for(V的每个邻接点W)//视野看得到的灯
if(!visited[W])//检测是否还有没点亮的
DFS(W);//递归调用
}
//类似树的先序遍历
若有N个顶点、E条边，时间复杂度是
用邻接表存储图，有O(N+E)//对每个点访问了一次，每条边也访问了一次
用邻接矩阵存储图，有O(N²)//V对应的每个邻接点W都要访问一遍

实例说明

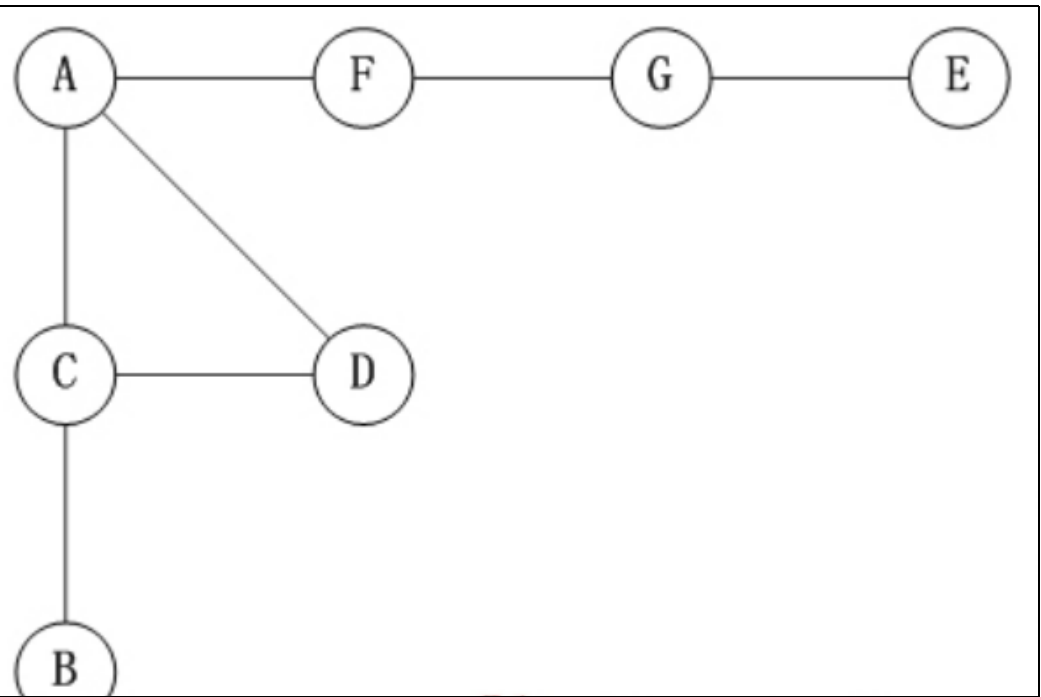
第1步：访问A。

第2步：访问(A的邻接点)C。在第1步访问A之后，接下来应该访问的是A的邻接点，即"C,D,F"中的一个。

但在本文的实现中，顶点ABCDEFG是按照顺序存储，C在"D和F"的前面，因此，先访问C。

第3步：访问(C的邻接点)B。在第2步访问C之后，接下来应该访问C的邻接点，即"B和D"中一个(A已经被

访问过，就不算在内)。而由于B在D之前，先访问B。

第4步：访问(C的邻接点)D。在第3步访问了C的邻接点B之后，B没有未被访问的邻接点；因此，返回到

访问C的另一个邻接点D。

第5步：访问(A的邻接点)F。 前面已经访问了A，并且访问完了"A的邻接点B的所有邻接点(包括递归的邻

接点在内)"；因此，此时返回到访问A的另一个邻接点F。

第6步：访问(F的邻接点)G。

第7步：访问(G的邻接点)E。

因此访问顺序是：A -> C -> B -> D -> F -> G -> E。

当然，上图是基于无向图，具体的代码在文章后面实现。

广度优先搜索

广度优先搜索算法(Breadth First Search)，又称为"宽度优先搜索"或"横向优先搜索"，简称BFS。

它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这

些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被

访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另

选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为

1,2…的顶点。

实例说明

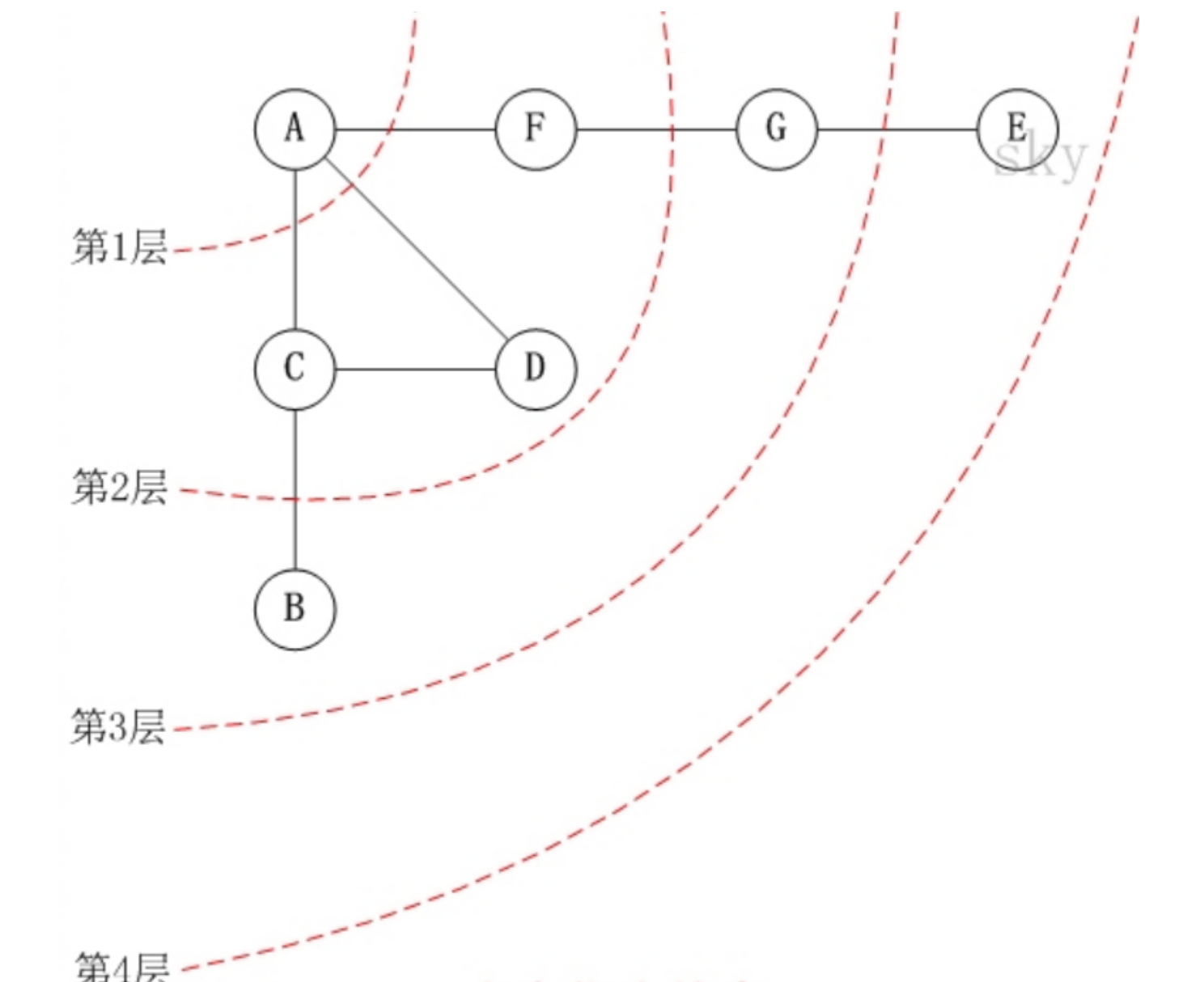
第1步：访问A。

第2步：依次访问C,D,F。在访问了A之后，接下来访问A的邻接点。前面已经说过，在本文实现中，顶点

ABCDEFG按照顺序存储的，C在"D和F"的前面，因此，先访问C。再访问完C之后，再依次访问D,F。

第3步：依次访问B,G。在第2步访问完C,D,F之后，再依次访问它们的邻接点。首先访问C的邻接点B，再

访问F的邻接点G。

第4步：访问E。在第3步访问完B,G之后，再依次访问它们的邻接点。只有G有邻接点E，因此访问G的邻

接点E。

因此访问顺序是：A -> C -> D -> F -> B -> G -> E。

6.2.3 图的遍历——为什么需要两种遍历

在不同的情况下效率不同

广度跟深度的区别

• 1. 深度是直接一条路走到黑，碰壁没路走了在返回
• 2. 广度是一圈一圈的扫描过去，虽然前面还有路也不会强行深入

6.2.4 图的遍历——图不连通怎么办

连通：如果从V到W存在一条(无向)路径，则称V与W是连通的

路径：V到W路径是一系列顶点{V,v1,v2,....,vn,W}的集合，其中任一对相邻的顶点间都有图中的边。

路径的长度是路径中的边数(如果带权(带权图)，则是所有边的权重和)。如果V到W之间的所有顶点都不同， 则称为简单路径(有回路就不是简单路径)

回路：起点等于终点的路径

连通图：图中任意两顶点均连通

连通分量：无向图的极大连通子图

• 1. 极大顶点数：再加1个顶点就不连通了
• 2. 极大边数：包含子图中所有顶点相连的所有边

对有向图：

//强连通：有向图中顶点V和W之间存在双向路径，则称V和W是强连通的(路径可以不同同一条，但是一定是连

通的)

//强连通图：有向图中任意两顶点均强连通

//强连通分量：有向图的极大强连通子图

//弱连通图：将强连通图的所有边的方向抹掉变成无向图就是连通的了

每调用一次DFS(V)，就把V所在的连通分量遍历了一遍,BFS也一样

void DFS(Vertex V){
visited[V] = true;
for(V的每个邻接点W)
if(!visited[W])
DFS(W);
}

遍历分量

void ListComponents(Graph G){
for(each V in G)
if(!visited[V]){
DFS(V);//or BFS(V)
}
}

6.3 应用实例：拯救007

void Save007(Graph G)
{
for(each V in G){
if(!visited[V] && FirstJump(V)){//这个FirstJump(V)是007第一跳有没有可能从孤岛
跳到V上有没有可能，有且没踩过就跳上去
answer = DFS(V);//or BFS(V)
if(answer == YES) break;0
}
}
if(answer == YES) output("Yes");
else output("No");
}

DFS算法

void DFS(Vertex V)
{
visited[V] = true;//表示鳄鱼头踩过了
for(V的每个邻接点W)
if(!visited[W])
DFS(W);//递归
}

改良版本

void DFS(Vertex V)
{
visited[V] = true;//表示鳄鱼头踩过了
if(IOsSafe(V)) answer = YES;
else{
for(each W in G )
if(!visited[W] && Jump(V,W)){//可以从V jump跳到这个w上面，作用是算V到W之间的距
离是不是小于007可以跳跃最大距离
answer = DFS(W);//递归
if(answer == YES) break;
}
}
return answer;
}

6.4 应用实例：六度空间(Six Degrees of Separation)

理论：

1. 你和任何一个陌生人之间所间隔的人不会超过6个
2. 给定社交网络图，请对每个节点计算符合"六度空间"理论的结点占结点总数的百分比

算法思路

1.对每个节点进行广度优先搜索

2.搜索过程中累计访问的节点数

3.需要记录"层"数,仅计算6层以内的节点数

void SDS()
{
for(each V in G){
count += BFS(V);
Output = (count/N);
}
}
//结合最初的BFS
void BFS(Vertex V)
{
visited[V] = true;count = 1;
Enqueue(V,Q);//压到队列里
while(!IsEmpty(Q)){
V = Dequeue(Q);//每次循环弹出一个节点
for(V的每个邻接点W)
if(!visited[W]){//没有访问过的去访问将其压入队列中
visited[W] = true;
Enqueue(W,Q);count++;
}
}return count;
}

另外的解决方案

int BFS(Vertex V)
{
vistex[V] = true;count = 1;
level = 0;last = V;
Enqueue(V,Q);
while(!IsEmpty(Q)){
V = Dequeue(Q);
for( V的每个邻接点W)
if(!visited[W]){
visited[W] = true;
Enqueue(W,Q);count++;
tail = W;
}
if(V == last ){
level++;last = tail;
}
}
return count++;
}