1 什么是学习率

2 学习率对网络的影响

3 学习率的设置

3.1 分段常数衰减（Piecewise Decay）

3.2 指数衰减（Exponential Decay）

3.3 自然指数衰减（Natural Exponential Decay）

3.4 多项式衰减（Polynomial Decay）

3.5 间隔衰减（Step Decay）

3.6 多间隔衰减（Multi Step Decay）

3.7 逆时间衰减（Inverse Time Decay）

3.8 Lambda衰减（Lambda Decay）

3.9 余弦衰减（Cosine Annealing Decay）

3.10 诺姆衰减（Noam Decay）

3.11 loss自适应衰减（Reduce On Plateau）

3.12 线性学习率热身（Linear Warm Up）

4 pytorch优化器与学习率设置

5 Transformers之自定义学习率动态调整

在我们刚刚接触深度学习时，对学习率只有一个很基础的认知，当学习率过大的时候会导致模型难以收敛，过小的时候会收敛速度过慢，其实学习率是一个十分重要的参数，合理的学习率才能让模型收敛到最小点而非局部最优点或鞍点。

1 什么是学习率

学习率是训练神经网络的重要超参数之一，它代表在每一次迭代中梯度向损失函数最优解移动的步长，通常用 η 表示。它的大小决定网络学习速度的快慢。在网络训练过程中，模型通过样本数据给出预测值，计算代价函数并通过反向传播来调整参数。重复上述过程，使得模型参数逐步趋于最优解从而获得最优模型。在这个过程中，学习率负责控制每一步参数更新的步长。合适的学习率可以使代价函数以合适的速度收敛到最小值。

2 学习率对网络的影响

梯度更新公式：

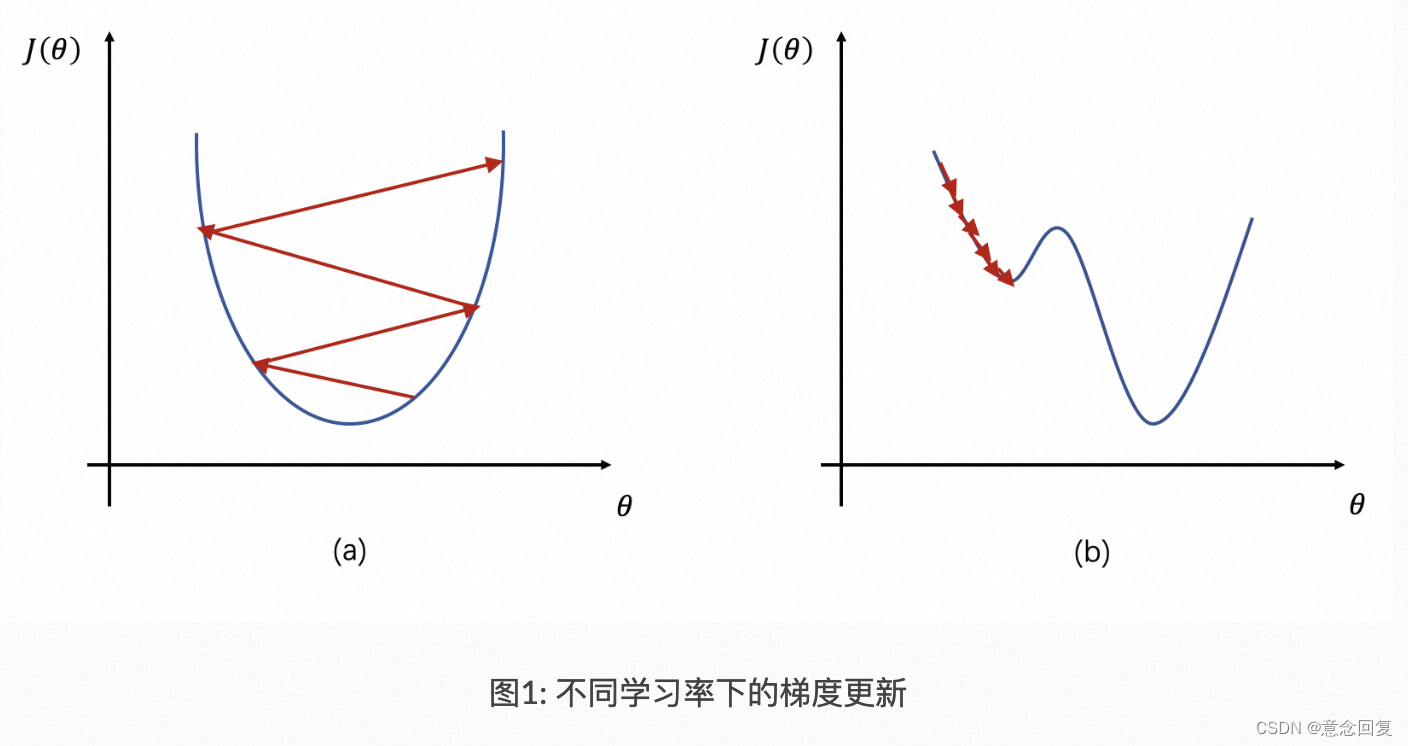
根据上述公式我们可以看到，如果学习率 η 较大，那么参数的更新速度就会很快，可以加快网络的收敛速度，但如果学习率过大，可能会导致参数在最优解附近震荡，代价函数难以收敛，甚至可能会错过最优解，导致参数向错误的方向更新，代价函数不仅不收敛反而可能爆炸（如图1a所示）。

如果学习率 η 较小，网络可能不会错过最优点，但是网络学习速度会变慢。同时，如果学习率过小，则很可能会陷入局部最优点（如图1b所示）。

因此，只有找到合适的学习率，才能保证代价函数以较快的速度逼近全局最优解。

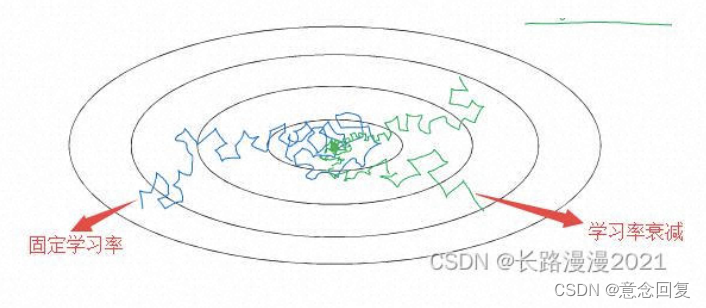
对于深度学习模型训练时，在梯度下降法中，固定学习率时，当到达收敛状态时，会在最优值附近一个较大的区域内摆动；而当随着迭代轮次的增加而减小学习率，会使得在收敛时，在最优值附近一个更小的区域内摆动。（之所以曲线震荡朝向最优值收敛，是因为在每一个mini-batch中都存在噪音）。如下图所示。

3 学习率的设置

设置学习率这个超参数总体上可以分为两种：人工调整和策略调整。

人工调整学习率一般是根据我们的经验值进行尝试，通常我们会尝试性的将初始学习率设为：0.1，0.01，0.001，0.0001等来观察网络初始阶段epoch的loss情况：

        如果训练初期loss出现梯度爆炸或NaN这样的情况（暂时排除其他原因引起的loss异常），说明初始学习率偏大，可以将初始学习率降低10倍再次尝试；
        如果训练初期loss下降缓慢，说明初始学习率偏小，可以将初始学习率增加5倍或10倍再次尝试；
        如果训练一段时间后loss下降缓慢或者出现震荡现象，可能训练进入到一个局部最小值或者鞍点附近。如果在局部最小值附近，需要降低学习率使训练朝更精细的位置移动；如果处于鞍点附件，需要适当增加学习率使步长更大跳出鞍点。
        如果网络权重采用随机初始化方式从头学习，有时会因为任务复杂，初始学习率需要设置的比较小，否则很容易梯度飞掉带来模型的不稳定(振荡)。这种思想也叫做Warmup，在预热的小学习率下，模型可以慢慢趋于稳定，等模型相对稳定后再选择预先设置的学习率进行训练,使得模型收敛速度变得更快，模型效果更佳。
        如果网络基于预训练权重做的微调(finetune)，由于模型在原数据集上已经收敛，有一个较好的起点，可以将初始学习率设置的小一些进行微调，比如0.0001。
策略调整学习率包括固定策略的学习率衰减和自适应学习率衰减，由于学习率如果连续衰减，不同的训练数据就会有不同的学习率。当学习率衰减时，在相似的训练数据下参数更新的速度也会放慢，就相当于减小了训练数据对模型训练结果的影响。为了使训练数据集中的所有数据对模型训练有相等的作用，通常是以epoch为单位衰减学习率。

在模型优化中，常用到的几种学习率衰减方法有：分段常数衰减、多项式衰减、指数衰减、自然指数衰减、余弦衰减、线性余弦衰减、噪声线性余弦衰减。

3.1 分段常数衰减（Piecewise Decay）

分段常数衰减需要事先定义好的训练次数区间，在对应区间置不同的学习率的常数值，一般情况刚开始的学习率要大一些，之后要越来越小，要根据样本量的大小设置区间的间隔大小，样本量越大，区间间隔要小一点。下图即为分段常数衰减的学习率变化图，横坐标代表训练次数，纵坐标代表学习率。

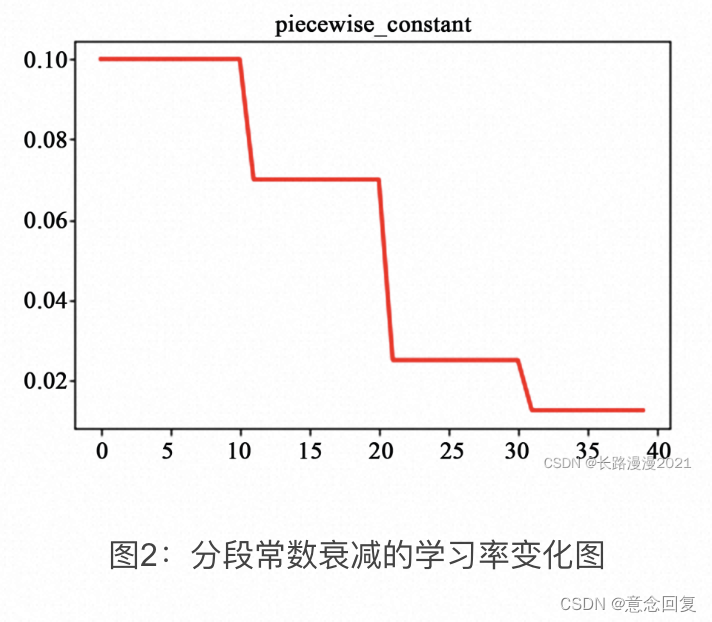
在不同的学习阶段指定不同的学习率，在每段内学习率相同。该过程可以举例说明为：

boundaries = [100, 200]  # 指定学习率改变的边界点为100和200
values = [1.0, 0.5, 0.1] # 指定不同区间下的学习率大小

learning_rate = 1.0  if epoch < 100 
learning_rate = 0.5  if 100 <= epoch < 200
learning_rate = 0.1  if epoch >= 200

3.2 指数衰减（Exponential Decay）

学习率随训练轮数成指数衰减，每次将当前学习率乘以给定的衰减率得到下一个学习率。指数衰减的公式可表示为：

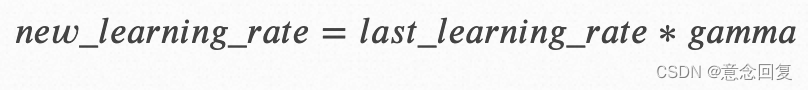
其中，𝑔𝑎𝑚𝑚𝑎为衰减率。

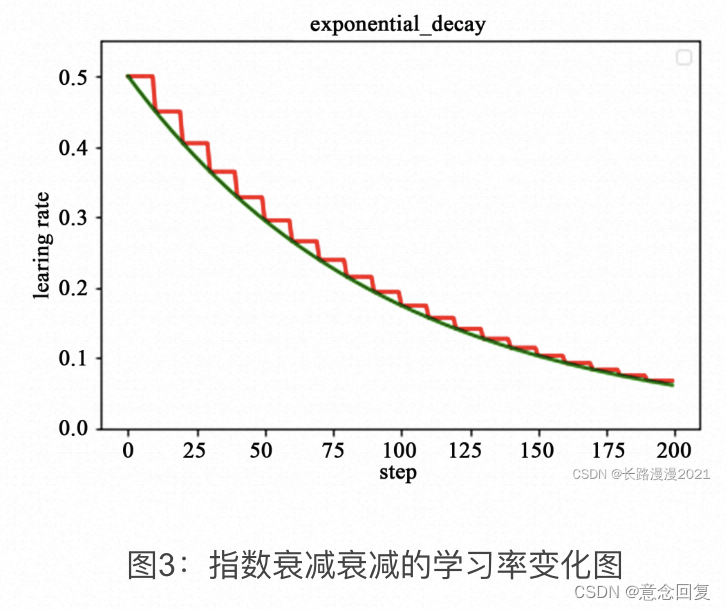
这种衰减方式简单直接，收敛速度快，是最常用的学习率衰减方式，如下图所示，绿色的为学习率随训练次数的指数衰减方式，红色的即为分段常数衰减，它在一定的训练区间内保持学习率不变。

3.3 自然指数衰减（Natural Exponential Decay）

每次将当前学习率乘以给定的衰减率的自然指数得到下一个学习率，故而其收敛的速度更快，一般用于相对比较容易训练的网络，便于较快的收敛。其公式表达为：

其中，𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔_𝑟𝑎𝑡𝑒 为初始学习率，𝑔𝑎𝑚𝑚𝑎为衰减率，𝑒𝑝𝑜𝑐ℎ为训练轮数。

下图为为分段常数衰减、指数衰减、自然指数衰减三种方式的对比图，红色的即为分段常数衰减图，阶梯型曲线。蓝色线为指数衰减图，绿色即为自然指数衰减图，很明可以看到自然指数衰减方式下的学习率衰减程度要大于一般指数衰减方式，有助于更快的收敛。

3.4 多项式衰减（Polynomial Decay）

通过多项式衰减函数，学习率从初始值逐渐衰减至最低学习率。其中，参数 𝑐𝑦𝑐𝑙𝑒 代表学习率下降后是否重新上升。若 𝑐𝑦𝑐𝑙𝑒=𝑇𝑟𝑢𝑒，则学习率衰减至最低后会重新上升到一定值，再降低至最低学习率并进行循环。若 𝑐𝑦𝑐𝑙𝑒=𝐹𝑎𝑙𝑠𝑒，则学习率从初始值单调递减至最低值。

若 𝑐𝑦𝑐𝑙𝑒=𝑇𝑟𝑢𝑒，其计算公式为：

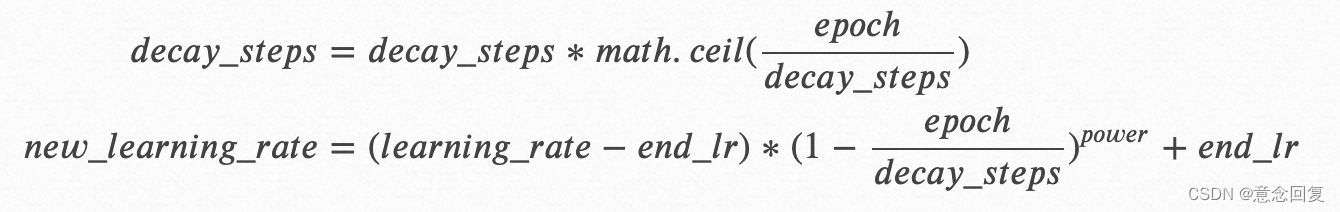
若 𝑐𝑦𝑐𝑙𝑒=𝐹𝑎𝑙𝑠𝑒，其计算公式为：

其中，𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔_𝑟𝑎𝑡𝑒 为初始学习率，𝑑𝑒𝑐𝑎𝑦_𝑠𝑡𝑒𝑝 为进行衰减的步长，𝑒𝑛𝑑_𝑙𝑟为最低学习率，𝑝𝑜𝑤𝑒𝑟为多项式的幂。

如下图所示，红色线代表学习率降低至最低后，一直保持学习率不变进行更新，绿色线代表学习率衰减到最低后，又会再次循环往复的升高降低。

3.5 间隔衰减（Step Decay）

学习率按照指定的轮数间隔进行衰减，该过程可举例说明为：

learning_rate = 0.5 # 学习率初始值
step_size = 30      # 每训练30个epoch进行一次衰减
gamma = 0.1         # 衰减率


learning_rate = 0.5    if epoch < 30 
learning_rate = 0.05   if 30 <= epoch < 60
learning_rate = 0.005  if 60 <= epoch < 90
...

3.6 多间隔衰减（Multi Step Decay）

学习率按特定间隔进行衰减，与间隔衰减的区别在于：间隔衰减的epoch间隔是单一且固定的，而多间隔衰减中的epoch间隔是预先指定的多间隔。该过程可举例说明为：

learning_rate = 0.5    # 学习率初始值
milestones = [30, 50]  # 指定轮数间隔
gamma = 0.1            # 衰减率

learning_rate = 0.5    if epoch < 30
learning_rate = 0.05   if 30 <= epoch < 50
learning_rate = 0.005  if 50 <= epoch
...

3.7 逆时间衰减（Inverse Time Decay）

学习率大小与当前衰减次数成反比。其计算公式如下：

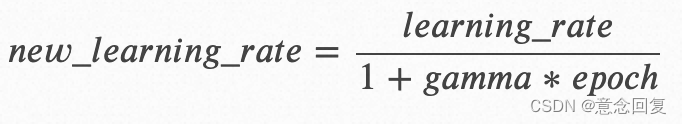
其中，𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔_𝑟𝑎𝑡𝑒为初始学习率，𝑔𝑎𝑚𝑚𝑎为衰减率，𝑒𝑝𝑜𝑐ℎ 为训练轮数。

3.8 Lambda衰减（Lambda Decay）

使用lambda函数来设置学习率，其中lambda函数通过epoch计算出一个因子，使用该因子乘以初始学习率。该衰减过程可参考如下例子：

learning_rate = 0.5                      # 学习率初始值
lr_lambda = lambda epoch: 0.95 ** epoch  # 定义lambda函数

learning_rate = 0.5              # 当epoch = 0时，0.5 * 0.95 ** 0 = 0.5
learning_rate = 0.475            # 当epoch = 1时，0.5 * 0.95 ** 1 = 0.475
learning_rate = 0.45125          # 当epoch = 2时，0.5 * 0.95 ** 2 = 0.45125
...

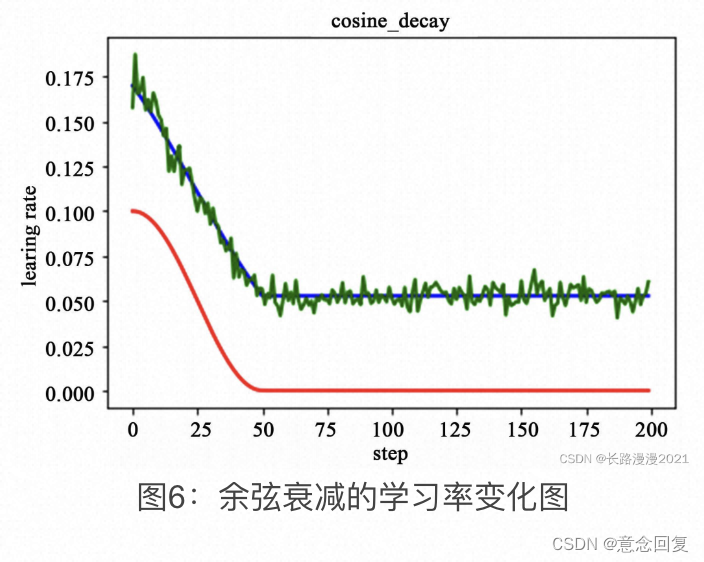
3.9 余弦衰减（Cosine Annealing Decay）

使用 cosine annealing 的策略来动态调整学习率，学习率随step数变化成余弦函数周期变化。该方法为论文 SGDR：Stochastic Gradient Descent with Warm Restarts 中cosine annealing动态学习率。学习率调整公式为：

其中，𝜂𝑚𝑎𝑥的初始值为学习率的初始值，𝑇𝑐𝑢𝑟是SGDR训练过程中的当前训练轮数。

如下图所示，红色即为标准的余弦衰减曲线，学习率从初始值下降到最低学习率后保持不变。蓝色的线是线性余弦衰减方式曲线，它是学习率从初始学习率以线性的方式下降到最低学习率值。绿色噪声线性余弦衰减方式。

3.10 诺姆衰减（Noam Decay）

诺姆衰减的计算方式如下：

其中，𝑑𝑚𝑜𝑑𝑒𝑙 代表模型的输入、输出向量特征维度，𝑤𝑎𝑟𝑚𝑢𝑝_𝑠𝑡𝑒𝑝𝑠 为预热步数，𝑙𝑒𝑎𝑟𝑛𝑖𝑛𝑔_𝑟𝑎𝑡𝑒 为初始学习率。更多细节请参考 attention is all you need。

3.11 loss自适应衰减（Reduce On Plateau）

当loss停止下降时，降低学习率。其思想是：一旦模型表现不再提升，将学习率降低 2-10 倍对模型的训练往往有益。此外，每降低一次学习率后，将会进入一个冷静期。在冷静期内不会监控loss变化也不会进行衰减。当冷静期结束后，会继续监控loss的上升或下降。

3.12 线性学习率热身（Linear Warm Up）

线性学习率热身是一种学习率优化策略，在正常调整学习率前，先逐步增大学习率。

当训练步数小于热身步数（warmup_steps）时，学习率 𝑙𝑟 按如下方式更新：

当训练步数大于等于热身步数（warmup_steps）时，学习率 𝑙𝑟为：

其中，𝑙𝑟为热身之后的学习率，𝑠𝑡𝑎𝑟𝑡_𝑙𝑟为学习率初始值，𝑒𝑛𝑑_𝑙𝑟为最终学习率，𝑒𝑝𝑜𝑐ℎ 为训练轮数。

4 pytorch优化器与学习率设置

pytorch优化器与学习率设置详解 - 知乎

torch.optim — PyTorch 2.0 documentation

torch.optim.lr_scheduler — PyTorch 2.0 documentation

5 Transformers之自定义学习率动态调整

Transformers之自定义学习率动态调整 - 知乎

参考

学习率：https://paddlepedia.readthedocs.io/en/latest/tutorials/deep_learning/model_tuning/learning_rate.html
图解 9 种Torch中常用的学习率调整策略：https://mp.weixin.qq.com/s/A-BkpToAr2ubhTnz_bvkpQ
如何配置神经网络的学习率：https://blog.csdn.net/weixin_39653948/article/details/105962154
炼丹手册——学习率设置：https://zhuanlan.zhihu.com/p/332766013
PyTorch优化器与学习率设置详解：https://zhuanlan.zhihu.com/p/435669796
Transformers之自定义学习率动态调整：https://zhuanlan.zhihu.com/p/466992867