文章目录
- 【 1.相关 】
- 自相关
- 互相关
- 【 2.匹配滤波 】
- 滤波器模型
- 有色噪声 时滤波器的特性
- 白噪声 时滤波器的特性
- 【 3.脉冲压缩】
- 时域脉冲压缩
- 频域脉冲压缩
- 【 4.模糊函数 】
- 【 5.四者之间的关系 】
- 相关和卷积之间的关系
- 【 6.参考文献 】
【 1.相关 】
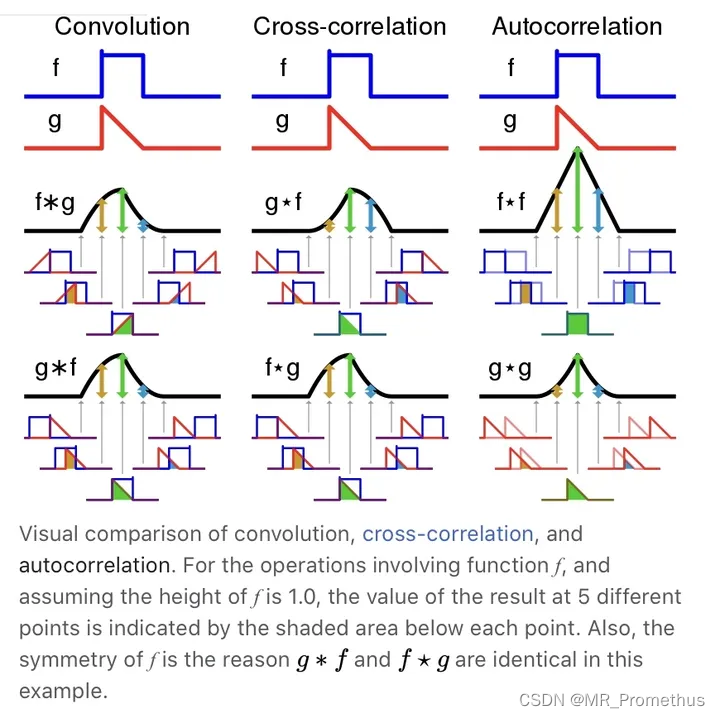
- 相关性表示一个信号平移 τ \tau τ 或 m 之后与另一个信号或者该信号本身的 相似程度。
- 相关函数是关于平移量的一个函数。
- 复数信号在做相关的时候,其中一个信号要取共轭,共轭取在前面的信号或者取在后面的信号都可以。
自相关
- 自相关:一个信号平移 τ \tau τ 或 m 之后与该信号本身的 相似程度/相关性。
- 不发生延迟(即
τ
=
0
\tau=0
τ=0 或
m
=
0
m=0
m=0)时,信号的自相关值达到最大。
连续自相关: R x x ( τ ) = ∫ − ∞ + ∞ x ( t ) x ( t − τ ) d t 连续自相关:R_{xx}(\tau)=\int_{-\infty}^{+\infty}x(t)x(t-\tau)dt 连续自相关:Rxx(τ)=∫−∞+∞x(t)x(t−τ)dt
离散自相关: R x x ( m ) = ∑ n = − ∞ + ∞ x ( n ) x ( n − m ) 离散自相关:R_{xx}(m)=\sum_{n=-\infty}^{+\infty}x(n)x(n-m) 离散自相关:Rxx(m)=n=−∞∑+∞x(n)x(n−m)
互相关
- 互相关:一个信号平移 τ \tau τ 或 m 之后与另一个信号的 相似程度/相关性。
- 互相关是有顺序的,即 R x y ( m ) ≠ R y x ( m ) R_{xy}(m)\neq R_{yx}(m) Rxy(m)=Ryx(m) 或者 R x y ( τ ) ≠ R y x ( τ ) R_{xy}(\tau)\neq R_{yx}(\tau) Rxy(τ)=Ryx(τ) 。
- x(t) 是偶函数的话,互相关与卷积的结果是一样的。
连续互相关:
R
x
y
(
τ
)
=
∫
−
∞
+
∞
x
(
t
)
y
(
t
−
τ
)
d
t
连续互相关:R_{xy}(\tau)=\int_{-\infty}^{+\infty}x(t)y(t-\tau)dt
连续互相关:Rxy(τ)=∫−∞+∞x(t)y(t−τ)dt
离散互相关:
R
x
y
(
m
)
=
∑
n
=
−
∞
+
∞
x
(
n
)
y
(
n
−
m
)
离散互相关:R_{xy}(m)=\sum_{n=-\infty}^{+\infty}x(n)y(n-m)
离散互相关:Rxy(m)=n=−∞∑+∞x(n)y(n−m)
【 2.匹配滤波 】
- 匹配滤波器 (Match Filter,MF) :当输人端出现信号与加性白噪声(此噪声不必是高斯的)时,使其输出信噪比最大的滤波器,就是一个与输入信号相 匹配 的最佳滤波器。
- 针对接收机而言,匹配滤波器是指其接收机的频率特性与发射信号的频谱特性相匹配。
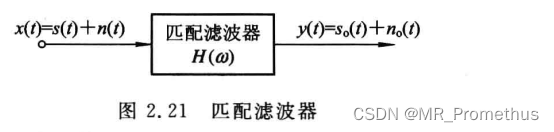
滤波器模型
- 设 线性时不变 滤波器的系统函数为 H(w),脉冲响应为 h(t)。假设滤波器的输入信号 x(t) 为 x ( t ) = s ( t ) + n ( t ) x(t)=s(t)+n(t) x(t)=s(t)+n(t),其中,s(t) 是能量为 E s E_s Es 的确知信号,n(t) 是 零均值平稳加性噪声 。
- 利用线性系统叠加定理,滤波器的输出信号 y(t) 为 y ( t ) = s o ( t ) + n o ( t ) y(t)=s_o(t)+n_o(t) y(t)=so(t)+no(t)。其中,输出 s o ( t ) s_o(t) so(t) 和 n o ( t ) n_o(t) no(t) 分别是滤波器对输入 s(t) 和 n(t) 的响应。假设滤波器输出信号 s o ( t ) s_o(t) so(t) 在 t = t 0 t=t_0 t=t0 时刻出现峰值。
-
α
\alpha
α 为任意非零常数,
P
n
(
w
)
P_n(w)
Pn(w) 为噪声的功率谱密度。
有色噪声 时滤波器的特性
传递函数: H ( ω ) = α S ∗ ( ω ) P n ( ω ) e − i ω t 0 传递函数:H(\omega)=\frac{\alpha{S}^*(\omega)}{P_n(\omega)}\mathrm{e}^{-\mathrm{i}\omega t_0} 传递函数:H(ω)=Pn(ω)αS∗(ω)e−iωt0
最大输出信噪比: SNR o = 1 2 π ∫ − ∞ ∞ ∣ S ( ω ) ∣ 2 P n ( ω ) d ω 最大输出信噪比:\text{SNR}_o=\frac{1}{2\pi}\int_{-\infty}^\infty\frac{|S(\omega)|^2}{P_n(\omega)}\text{d}\omega 最大输出信噪比:SNRo=2π1∫−∞∞Pn(ω)∣S(ω)∣2dω
白噪声 时滤波器的特性
- 滤波器输入白噪声功率谱密度 P n ( w ) = N 0 2 P_n(w)=\frac{N_0}{2} Pn(w)=2N0。
- 传递函数 和 脉冲响应函数
传递函数: H ( ω ) = k S ∗ ( ω ) e − j ω t 0 , k = 2 α N 0 传递函数:H(\omega) = kS ^{\ast} (\omega)\mathrm e^{-j\omega t_0},k=\frac{2\alpha}{N_0} 传递函数:H(ω)=kS∗(ω)e−jωt0,k=N02α
脉冲响应函数: h ( t ) = k s ∗ ( t 0 − t ) 脉冲响应函数:h(t)=ks^*(t_0-t) 脉冲响应函数:h(t)=ks∗(t0−t) - 最大输出信噪比
最大输出信噪比: S N R o = 1 2 π ∫ − ∞ ∞ ∣ S ( ω ) ∣ 2 N 0 2 d ω = 2 E s N 0 最大输出信噪比:\mathrm{SNR}_{o}={\frac{1}{2\pi}}\int_{-\infty}^{\infty}{\frac{\left|\mathrm{S}({\omega})\right|^{2}}{\frac{N_{0}}{2}}}\mathrm{d}{\omega}={\frac{2E_{s}}{N_{0}}} 最大输出信噪比:SNRo=2π1∫−∞∞2N0∣S(ω)∣2dω=N02Es
由此可见,匹配滤波器输出端的峰值瞬时信号功率与噪声的平均功率之比SNR。等于两倍的输人信号能量除以输人噪声功率。也就是说,匹配滤波器输出最大信噪比仅依赖于信号能量和输人噪声功率,而与雷达使用的波形无关。 - 简化的 传递函数 和 脉冲响应函数
非零常数 k 表示滤波器的相对放大量,因为我们关心的是滤波器的频率特性形状,而不是它的相对大小,所以在讨论中通常取 k=1。而且在讨论匹配滤波器时,时延 t 0 t_0 t0 可以不予考虑,则有
传递函数(简化后): H ( ω ) = S ∗ ( ω ) 传递函数(简化后):H(\omega) = S ^{\ast} (\omega) 传递函数(简化后):H(ω)=S∗(ω)
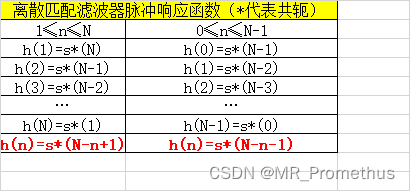
脉冲响应函数(简化后): h ( t ) = s ∗ ( − t ) 脉冲响应函数(简化后):h(t)=s^*(-t) 脉冲响应函数(简化后):h(t)=s∗(−t) - 对于离散信号匹配滤波器的脉冲响应函数,则如下表所示
【 3.脉冲压缩】
- 脉冲压缩处理的信号:大时宽带宽积信号。(脉冲压缩信号的大时宽带宽积的性能,大多是通过信号的非线性相位调制获得的,如脉宽内线性调频、非线性调频、频率编码和相位编码等)
- 脉冲压缩的目的:雷达发射脉冲的时宽 τ \tau τ 越大则平均功率越大,探测距离越远,但是雷达的距离分辨力 Δ R = c τ 2 \Delta R=\frac{c\tau}{2} ΔR=2cτ 越不精确。大时宽带宽积信号的出现,就可以使得雷达在发射端发射大时宽信号以保证足够远的探测距离,而在接收端通过脉冲压缩将接收到的大时宽脉冲信号压缩成窄脉冲信号,以保证足够精确的距离分辨力。这就使得雷达既可以发射宽脉冲以提高平均功率和雷达的检测能力,又能保持窄脉冲的距离分辨率。
- 脉冲压缩处理的过程:将宽脉冲信号压缩成窄脉冲信号。
- 雷达几乎都是在数字域进行脉压处理的,脉冲压缩本身就是实现信号的匹配滤波,只是在模拟域一般称匹配滤波,而在数字域称为脉冲压缩。
时域脉冲压缩
- 时域数字脉冲压缩是信号
s
(
n
)
s(n)
s(n) 与匹配滤波器 脉冲响应的时域线性卷积。
s o ( n ) = s ( n ) ∗ h ( n ) = ∑ k = 0 M − 1 s ( k ) h ( n − k ) = ∑ k = 0 M − 1 h ( k ) s ( n − k ) s_o(n)=s(n)*h(n)=\sum\limits_{k=0}^{M-1}s(k)h(n-k)=\sum\limits_{k=0}^{M-1}h(k)s(n-k) so(n)=s(n)∗h(n)=k=0∑M−1s(k)h(n−k)=k=0∑M−1h(k)s(n−k)
频域脉冲压缩
-
根据傅里叶变换的性质:时域卷积相当于频域乘积,则 s o ( n ) = s ( n ) ∗ h ( n ) = I F F T [ S ( w ) H ( w ) ] s_o(n)=s(n)*h(n)=IFFT[S(w)H(w)] so(n)=s(n)∗h(n)=IFFT[S(w)H(w)]。
-
而匹配滤波器的单位脉冲响应h(n)为输入信号 s(n) 的镜像共轭,即 H ( w ) = S ∗ ( w ) H(w)=S^*(w) H(w)=S∗(w),故:
s o ( n ) = I F F T [ S ( w ) S ∗ ( w ) ] = I F F T [ ∣ S ( w ) ∣ 2 ] s_o(n)=IFFT[S(w)S^*(w)]=IFFT[|S(w)|^2] so(n)=IFFT[S(w)S∗(w)]=IFFT[∣S(w)∣2] -
两种实现方式的对比
当要求较小的脉压比时,经常采用时域相关的处理方式;当要求较大的脉压比时,通常利用FFT在频域实现。
对于N点的输入信号,运用时域法需要进行 N 2 N^2 N2 次复数相乘运算,而利用频域法可以大大减少运算量。但是频域法需要对N进行扩展,而时域法则不需要。此外,时域法具有设计方法成熟、实现简单、成本较低廉的优势。
【 4.模糊函数 】
- 正形模糊函数:从分辨角度出发定义的模糊函数。
正形模糊函数: χ ( τ , f d ) = ∫ − ∞ ∞ u ( t ) u ⋆ ( t + τ ) e i 2 π f d t d t 正形模糊函数:\chi(\tau,f_d)=\int_{-\infty}^{\infty}u(t)u^{\star}(t+\tau)\mathrm{e}^{\text{i}2\pi f_d t}\mathrm{d}t 正形模糊函数:χ(τ,fd)=∫−∞∞u(t)u⋆(t+τ)ei2πfdtdt
利用帕塞瓦尔定理以及傅里叶变换的性质,正形模糊函数的另一种形式。
χ ( τ , f d ) = ∫ − ∞ ∞ U ( f − f d ) U ∗ ( f ) e − i 2 π f τ d f \chi(\tau,f_d)=\int_{-\infty}^{\infty}U(f-f_d)U^*(f)\mathrm{e}^{-i2\pi f\tau}\mathrm{d}f χ(τ,fd)=∫−∞∞U(f−fd)U∗(f)e−i2πfτdf - 负形模糊函数:从匹配滤波的输出出发定义的模糊函数。
负形模糊函数: χ ( τ , f d ) = ∫ − ∞ ∞ u ( t ) u ⋆ ( t − τ ) e i 2 π f d t d t 负形模糊函数:\chi(\tau,f_d)=\int_{-\infty}^{\infty}u(t)u^{\star}(t-\tau)\mathrm{e}^{\text{i}2\pi f_d t}\mathrm{d}t 负形模糊函数:χ(τ,fd)=∫−∞∞u(t)u⋆(t−τ)ei2πfdtdt
【 5.四者之间的关系 】
相关和卷积之间的关系
- 相关与卷积计算的不同在于相关计算不用进行翻转,直接与延时后的信号进行计算,而卷积要与翻转后再延时的信号进行计算。
- x ( t ) ∗ y ( − t ) = ∫ − ∞ ∞ x ( τ ) y [ − ( t − τ ) ] d τ = ∫ − ∞ ∞ x ( τ ) y ( τ − t ) d τ = R x y ( τ ) x(t)*y(-t)=\int_{-\infty}^{\infty}x(\tau)y[-(t-\tau)]d\tau=\int_{-\infty}^{\infty}x(\tau)y(\tau-t)d\tau=R_{xy}(\tau) x(t)∗y(−t)=∫−∞∞x(τ)y[−(t−τ)]dτ=∫−∞∞x(τ)y(τ−t)dτ=Rxy(τ)