在基础统计学，或者是计量经济学里面，需要对回归问题进行一些违背经典假设的检验，例如多重共线性、异方差、自相关的检验。这些检验用stata，r，Eviews什么都很简单，但是用python很多人都不会。下面就带大家实践一个回归案例完整版，看一下怎么实现。

---

回归案例 

导入包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
pd.set_option('display.float_format', lambda x: '{:.4f}'.format(x))

读取数据，设定时间索引

df=pd.read_excel('数据.xlsx').dropna(axis=1).set_index('year')
df

数据量不大

---

描述性统计 

df.describe().T

画散点图

y = df['agriculture']
x_cols = ['primium', 'agrloans', 'product', 'employ', 'pay']
x = df[x_cols]
fig = plt.figure(figsize=(8,4), dpi=128)  
for i in range(5):
    plt.subplot(2,3,i + 1)  # 2行3列子图
    sns.scatterplot(x=x.iloc[:, i], y=y)
    #plt.ylabel(column[i], fontsize=12)
    #plt.xticks([])
plt.tight_layout()
plt.savefig('散点图.jpg',dpi=128)
plt.show()

 

 可以看到五个自变量其中除了employ外，其他和agriculture都是正相关

column = df.columns.tolist() # 列表头
fig = plt.figure(figsize=(6,6), dpi=128)  # 指定绘图对象宽度和高度
for i in range(6):
    plt.subplot(3,2,i + 1)  # 2行3列子图
    sns.boxplot(data=df.iloc[:,i].to_numpy(), orient="v",width=0.5)  # 箱式图
    plt.ylabel(column[i], fontsize=12)
    plt.xticks([])
plt.tight_layout()
plt.savefig('箱线图.jpg',dpi=128)
plt.show()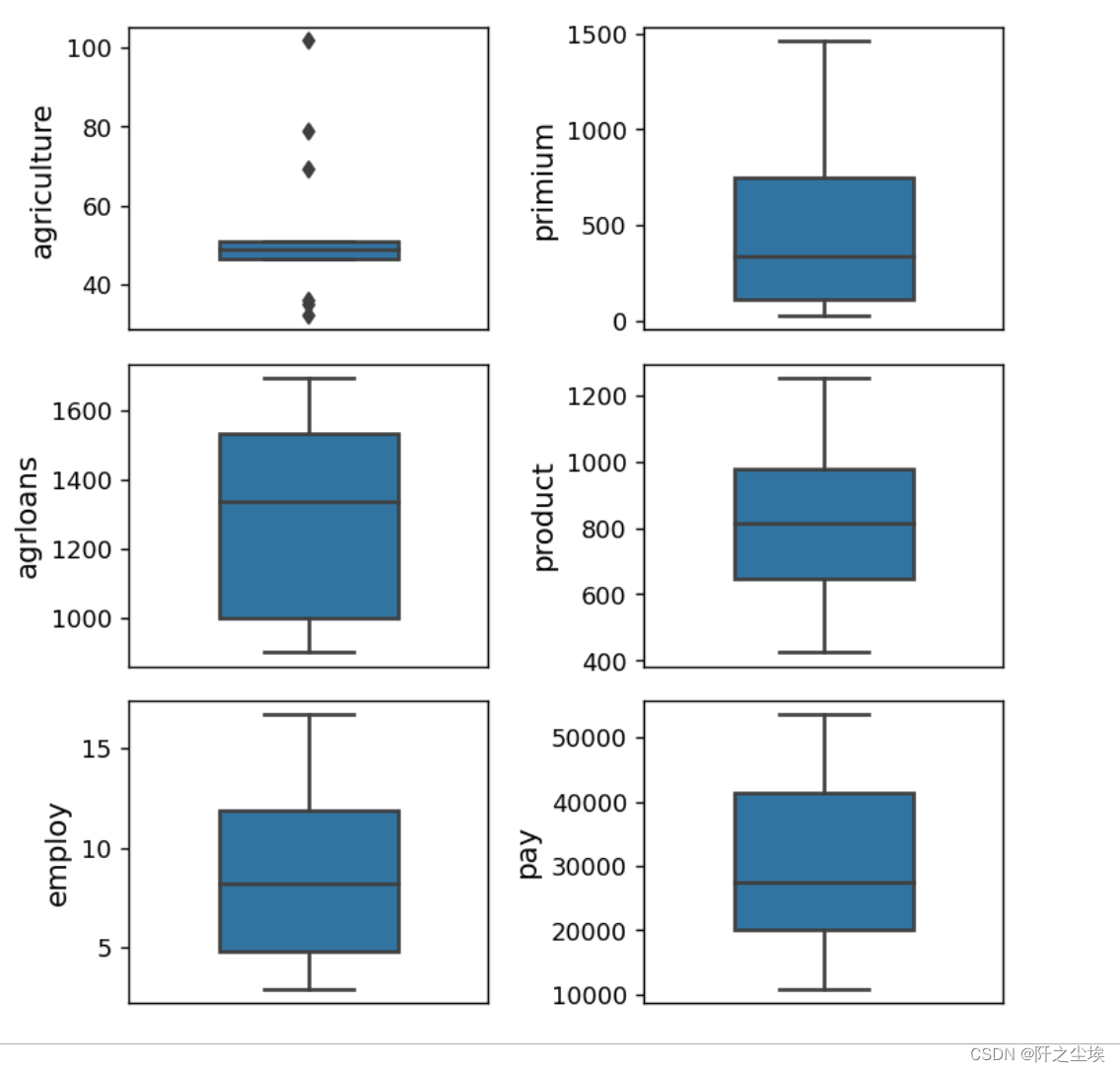

 

除了y自己外，其他的x的分布都较为对称，符合正态分布的假定¶

---

相关性分析

计算相关系数

df.corr()

plt.figure(figsize=(7,5),dpi=128)
sns.heatmap(df.corr().round(2), cmap='coolwarm', annot=True, annot_kws={"size": 10})
plt.savefig('相关系数.jpg')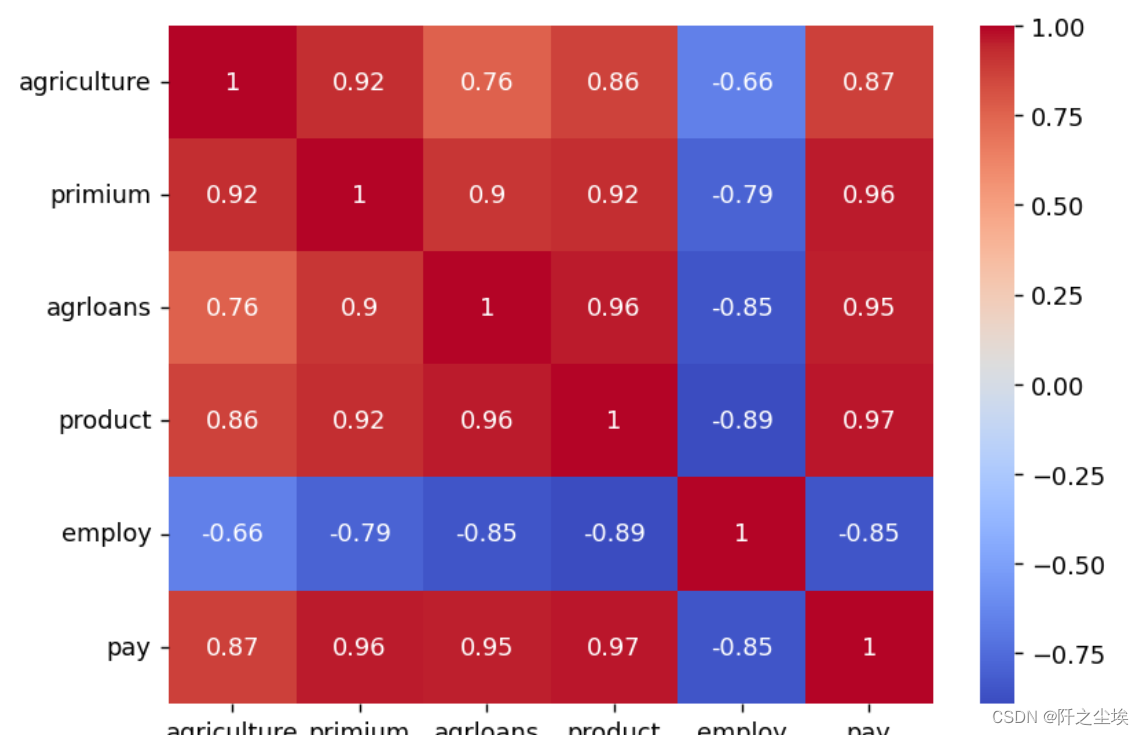

 

 

employ和其他变量都是负相关，agriculture和x之间都有高度的相关性，但是X们间也存在高度的相关，例如primium和其他四个x相关系数都高达0.9以上，

说明模型可能存在多重共线性。

---

OLS，多元线性回归

model = smf.ols('agriculture~primium+agrloans+product+employ+pay', data=df)
model = model.fit()
model.summary()

 

模型的拟合优度高达96%，调整后的R2为0.945。说明这几个解释变量能高度解释y的变化.整体的F值为45.30，远超临界值，说明模型整体很显著。

在0.05 的显著性水平下，除了pay，其他四个变量都是显著的，说明他们的变化对y产生了显著性影响。

再来看单个变量的系数，其中employ系数为正，agrloans系数负，这些不符合理论期望，应该是模型存在多重共线性导致的¶

计算方差膨胀因子，查看多重共线性。

---

VIF计算

def VIF_calculate(df_all,y_name):
    x_cols=df.columns.to_list()
    x_cols.remove(y_name)
    
    def vif(df_exog,exog_name):
        exog_use = list(df_exog.columns)
        exog_use.remove(exog_name)
        model=smf.ols(f"{exog_name}~{'+'.join(list(exog_use))}",data=df_exog).fit()
        return 1./(1.-model.rsquared)

    df_vif=pd.DataFrame()
    for x in x_cols:
        df_vif.loc['VIF',x]=vif(df_all[x_cols],x)
        
    df_vif.loc['tolerance']=1/df_vif.loc['VIF']
    df_vif=df_vif.T.sort_values('VIF',ascending=False)
    df_vif.loc['mean_vif']=df_vif.mean()
    return df_vif

VIF_calculate(df,'agriculture')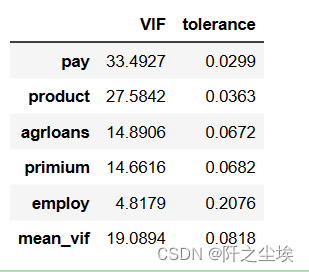

 一般认为VIF值大于10，模型就会存在多重共线性。除了employ变量，其他四个变量之间都存在多重共线性的问题

---

残差检验

plt.rcParams ['font.sans-serif'] =['SimHei']
plt.rcParams['axes.unicode_minus']=False
 
x=model.fittedvalues;y=model.resid
 
plt.subplots(1,2,figsize=(8,3),dpi=128)
plt.subplot(121)
plt.scatter(model.fittedvalues,model.resid)
plt.xlabel('拟合值')
plt.ylabel('残差')
plt.title('(a)残差值与拟合值图',fontsize=15)
plt.axhline(0,ls='--')
 
ax2=plt.subplot(122)
pplot=sm.ProbPlot(model.resid,fit=True)
pplot.qqplot(line='r',ax=ax2,xlabel='期望正态值',ylabel='标准化的观测值')
ax2.set_title('(b)残差正态Q-Q图',fontsize=15)
plt.show()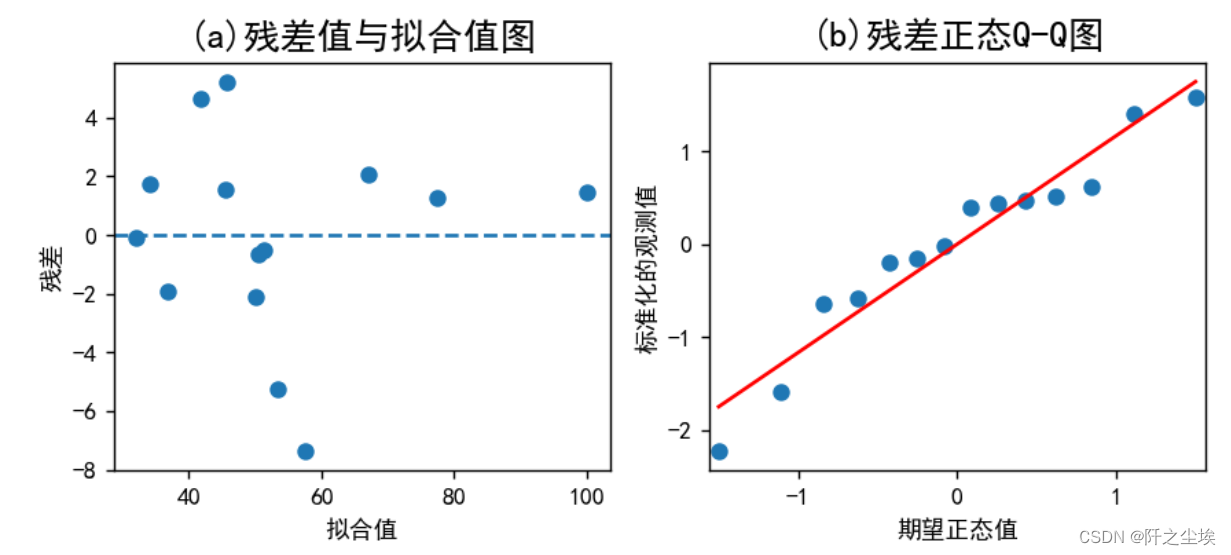

 

残差均匀分布在0轴附近，模型不存在异方差等问题

---

异方差的white检验

from statsmodels.stats.diagnostic import het_white
wh = het_white(model.resid, model.model.exog)
print('LM Statistic: {:.3f}'.format(wh[0]))
print('LM p-value: {:.3f}'.format(wh[1]))
#print('F Statistic: {:.3f}'.format(wh[2]))   print('F p-value: {:.3f}'.format(wh[3]))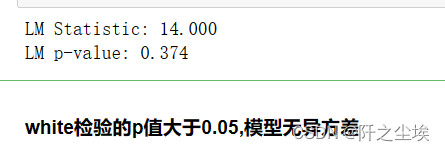

---

自相关的DW检验 

from statsmodels.stats.stattools import durbin_watson
dw = durbin_watson(model.resid)
print('DW statistic: {:.4f}'.format(dw))

 

---

 

下面处理多重共线性的问题

出现多重共线性问题时，可以采取以下几种方法进行处理：

1.删除相关性较强的变量。如果两个或多个自变量之间存在高度相关性，则可能会导致多重共线性问题。可以通过计算自变量之间的相关系数矩阵，然后删除其中相关性较强的变量，以降低共线性的影响。

2.主成分分析（PCA）。主成分分析可以将多个相关性较强的自变量转化为少数几个不相关的主成分，从而降低共线性的影响。可以使用Python中的sklearn.decomposition.PCA类进行主成分分析。

3.岭回归（Ridge Regression）。岭回归是一种正则化方法，可以通过在损失函数中增加一个惩罚项来避免过拟合。在存在多重共线性的情况下，使用岭回归可以降低模型方差，提高模型的泛化性能。

4.Lasso回归（Lasso Regression）。Lasso回归也是一种正则化方法，可以通过对回归系数的L1范数进行惩罚来实现特征选择和降维。Lasso回归可以通过缩小相关性较强的自变量的系数来降低多重共线性的影响。

5.收集更多数据。如果多重共线性问题来自于数据样本的局限性，那么可以通过收集更多的数据来缓解该问题。

（经济学应该只学了岭回归，就用这个吧）

岭回归

y = df['agriculture']
X = df[['primium', 'agrloans', 'product', 'employ', 'pay']]
from sklearn.linear_model import Ridge
model_ride = Ridge(alpha=10)
#拟合模型
model_ride.fit(X, y)
#计算测试集上的拟合优度
model_ride.score(X, y)

#模型截距
model_ride.intercept_

 

#模型系数 
#数据框展示系数
pd.DataFrame(model_ride.coef_, index=X.columns, columns=['Coefficient'])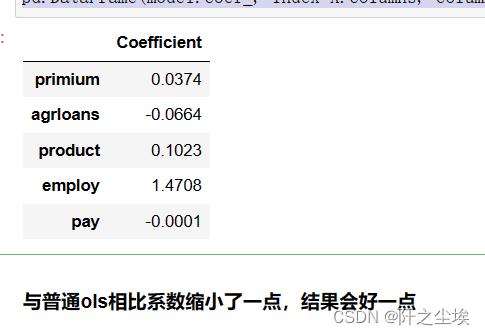

 

 

---

（PS，回归结果的导出储存）

我们上面的ols回归的那个图，怎么存到excel表里面导出来呢？

我写了一个函数，直接可以存回归模型的结果，还可以批量存回归模型。

def 储存(writer,model,model_name='model_SH1'):
    df1 = pd.DataFrame(model.summary().tables[0])
    df2 = pd.DataFrame(model.summary().tables[1])
    df3 = pd.DataFrame(model.summary().tables[2])
    df1.to_excel(writer, sheet_name=model_name, startrow=0, startcol=0, header=False, index=False)
    df2.to_excel(writer, sheet_name=model_name, startrow=df1.shape[0]+1, startcol=0, header=False, index=False)
    df3.to_excel(writer, sheet_name=model_name, startrow=df1.shape[0]+df2.shape[0]+2, startcol=0, header=False, index=False)

三个参数，一个是pandas的excel表对象，一个是模型变量，一个是模型名称。

使用如下：

model_list=['model']
with pd.ExcelWriter('回归表.xlsx') as writer:
    for model_name in model_list:
        model=eval(model_name)
        储存(writer,model=model,model_name=model_name)

把你模型的变量名称用字符串传入列表，然后运行就行，生成一个excel工作簿。一个模型就存在一个sheet里面，有几个模型就有几个sheet。

这里只有一个模型，所以只有一个sheet表：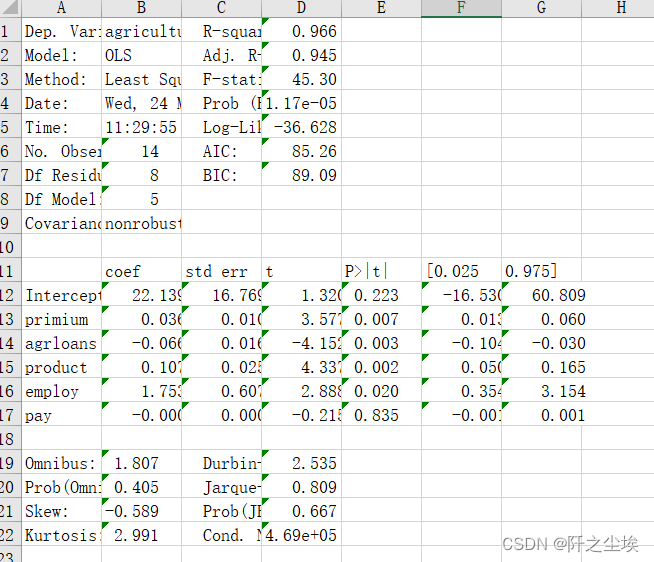

 和上面的ols结果是一样的。