一、新单元:图
-
Quiz 1包含lecture01到lecture08,关注数据结构和排序
-
今天开始新单元,lecture09-lecture14,关注图算法
二、图应用
-
图无处不在
-
任何网络系统都存在有向连接图
-
比如:路网、计算机网络、社交网络
-
任何离散系统的状态空间都可以用过渡图表示
-
比如:puzzle & games like Chess, Tetris, Rubik’s cube
-
比如:应用流,声明
三、图定义

-
图 G = ( V , E ) G=(V,E) G=(V,E)是一组点V和一组顶点的对 E ⊆ V × V E\subseteq V\times V E⊆V×V
-
有向边是有序对,比如, ( u , v ) , u , v ∈ V (u,v),u,v \in V (u,v),u,v∈V
-
无向边是无序对,比如, { u , v } , u , v ∈ V \{u,v\},u,v\in V {u,v},u,v∈V,比如: ( u , v ) 和 ( v , u ) (u,v)和(v,u) (u,v)和(v,u)
-
在这个类中,我们假设所有图是简单的:
-
边是去重的,比如(u,v)仅在E(尽管(v,u)可能出现)中出现一次,并且
-
边是非重复点的组合,比如: u ≠ v , ( u , v ) ∈ E u\ne v,(u,v)\in E u=v,(u,v)∈E
-
简单暗示着: ∣ E ∣ = O ( ∣ V ∣ 2 ) |E|=\mathcal{O}(|V|^2) ∣E∣=O(∣V∣2),因为无向: ∣ E ∣ = O ( ∣ V ∣ 2 ) |E|=\mathcal{O}(|V|^2) ∣E∣=O(∣V∣2),有向: ∣ E ∣ = O ( 2 ∣ V ∣ 2 ) |E|=\mathcal{O}(2|V|^2) ∣E∣=O(2∣V∣2)
-
四、相邻集合
-
u ∈ V , u 的出向相邻: A d j + ( u ) = { v ∈ V ∣ ( u , v ) ∈ E } u\in V,u的出向相邻:Adj^+(u)=\{v\in V|(u,v)\in E\} u∈V,u的出向相邻:Adj+(u)={v∈V∣(u,v)∈E}
-
u ∈ V , u 的入向相邻: A d j − ( u ) = v ∈ V ∣ ( u , v ) ∈ E u\in V,u的入向相邻:Adj^-(u)={v\in V|(u,v)\in E} u∈V,u的入向相邻:Adj−(u)=v∈V∣(u,v)∈E
-
顶点u的出度, u ∈ V , d e g + ( u ) = ∣ A d j + ( u ) ∣ u\in V,deg^+(u)=|Adj^+(u)| u∈V,deg+(u)=∣Adj+(u)∣
-
顶点u的出度, u ∈ V , d e g − ( u ) = ∣ A d j − ( u ) ∣ u\in V,deg^-(u)=|Adj^-(u)| u∈V,deg−(u)=∣Adj−(u)∣
-
对于无向图, A d j − ( u ) = A d j + ( u ) , d e g − ( u ) = d e g + ( u ) Adj^-(u)=Adj^+(u),deg^-(u)=deg^+(u) Adj−(u)=Adj+(u),deg−(u)=deg+(u)
-
删除上标默认是出向,比如, A d j ( u ) = A d j + ( u ) , d e g ( u ) = d e g + ( u ) Adj(u)=Adj^+(u),deg(u)=deg^+(u) Adj(u)=Adj+(u),deg(u)=deg+(u)
五、图的表达
-
为了存储图 G = ( V , E ) G=(V,E) G=(V,E),我们需要存储外向边 A d j ( u ) , u ∈ V Adj(u),u\in V Adj(u),u∈V
-
首先,需要一个集合数据结构 A d j Adj Adj来映射u到 A d j ( u ) Adj(u) Adj(u)
-
然后对于每个u,需要存储 A d j ( u ) Adj(u) Adj(u)到其他数据结构——邻接表
-
通常对Adj使用直接访问数组或哈希表,因为想通过顶点快速查找
-
通常对每个Adj(u)使用数组或链表,因为通常只需要迭代
-
通用表达: A d j 尺寸为 Θ ( ∣ V ∣ ) ,每个 A d j ( u ) 尺寸为 Θ ( d e g ( u ) ) Adj尺寸为\Theta(|V|),每个Adj(u)尺寸为\Theta(deg(u)) Adj尺寸为Θ(∣V∣),每个Adj(u)尺寸为Θ(deg(u))
-
因为由handshaking lemma得知 ∑ u ∈ V d e g ( u ) ≤ 2 ∣ E ∣ \sum_{u\in V}deg(u)\le2|E| ∑u∈Vdeg(u)≤2∣E∣,图存储空间为 Θ ( ∣ V ∣ + ∣ E ∣ ) \Theta(|V|+|E|) Θ(∣V∣+∣E∣)
-
因此,对于图算法,线性时间意味着 Θ ( ∣ V ∣ + ∣ E ∣ ) \Theta(|V|+|E|) Θ(∣V∣+∣E∣),与图尺寸呈线性
六、举例
- 例1和例2假设顶点标记为 { 0 , 1 , . . . , ∣ V ∣ − 1 } \{0,1,...,|V|-1\} {0,1,...,∣V∣−1},因此可以对Adj使用直接访问数组,存储Adj(u)到数组。例3对Adj使用哈希表。

- 注意在无向图中,连接是对称的,因为每个边算作两次出向
七、路径
-
路径是点的序列 p = ( v 1 , v 2 , . . . , v k ) , ( v i , v i + 1 ) ∈ E , 1 ≤ i < k p=(v_1,v_2,...,v_k),(v_i,v_{i+1})\in E,1\le i\lt k p=(v1,v2,...,vk),(vi,vi+1)∈E,1≤i<k
-
如果没有重复点,路径是简单的
-
长度 l ( p ) l(p) l(p)是路径p中边的个数
-
距离 δ ( u , v ) , 从 u ∈ V 到 v ∈ V \delta(u,v),从u\in V到v \in V δ(u,v),从u∈V到v∈V,表示u到v之间所有路径长度的最小值,比如:从u到v之间最短路径的长度,(按照惯例, δ ( u , v ) = ∞ \delta(u,v)=\infty δ(u,v)=∞,如果u与v不相连)
八、图路径问题
-
有许多你可能想解决的,与图路径有关的问题
-
SINGLE_PAIR_REACHABILITY(G, s, t):G中是否存在路径,从 s ∈ V 到 t ∈ V s\in V到t \in V s∈V到t∈V
-
SINGLE_PAIR_SHORTEST_PATH(G, s, t):返回距离 δ ( s , t ) \delta(s,t) δ(s,t),以及 G = ( V , E ) G=(V,E) G=(V,E)中从 s ∈ V 到 t ∈ V s\in V到t \in V s∈V到t∈V最短路径
-
SINGLE_PAIR_SHORTEST_PATHS(G,s):返回 δ ( s , v ) , v ∈ V \delta(s,v),v\in V δ(s,v),v∈V,以及一个最短路径树(包含从s到每个 v ∈ V v\in V v∈V的最短路径)
-
上面的每个问题都至少和上面的每个问题一样难,解决完一个低级问题,可以把它当作黑盒来解决任意更高级的问题
-
不会展示算法来解决所有这些问题
-
而是,展示一个算法,耗时 O ( ∣ V ∣ + ∣ E ∣ ) \mathcal{O}(|V|+|E|) O(∣V∣+∣E∣)来解决最难的
九、最短路径树
-
对于图中每个顶点,如何从源点s返回一条最短路径?
-
一些路径有长度 Ω ( ∣ V ∣ ) \Omega(|V|) Ω(∣V∣),因此返回每条路需要 Ω ( ∣ V ∣ 2 ) \Omega(|V|^2) Ω(∣V∣2)
-
对于所有 v ∈ V v\in V v∈V,存储它的parent P ( v ) P(v) P(v),从s出发最短路径上第二个到最后一个点
-
让P(s)为null(从s到s,最短路径上没有第二个到最后一个点)
-
parent集合构成了最短路径树,尺寸为 O ( ∣ V ∣ ) \mathcal{O}(|V|) O(∣V∣)
(例如,从每个点(s点可达)来返回到s的反向最短路径)
十、广度优先查找(BFS)
-
如何计算 δ ( s , v ) \delta(s,v) δ(s,v)和 P ( v ) P(v) P(v), v ∈ V v\in V v∈V?
-
存储 δ ( s , v ) \delta(s,v) δ(s,v)和 P ( v ) P(v) P(v)到集合数据结构,对应点v距离和parent
-
如果没有路径从s都v,不会存储v到P中,并设 δ ( s , v ) = ∞ \delta(s,v)=\infty δ(s,v)=∞
-
按距离升序探索图中点
-
目标:计算层级集合 L i = { v ∣ v ∈ V 且 d ( s , v ) = i } L_i=\{v|v\in V且d(s,v)=i\} Li={v∣v∈V且d(s,v)=i},所有点位于距离i
-
声明:每个点 v ∈ L i v\in L_i v∈Li,必须与点 u ∈ L i − 1 u\in L_{i-1} u∈Li−1相邻(比如, v ∈ A d j ( u ) v\in Adj(u) v∈Adj(u))
-
声明:在 L j L_j Lj(j<i)中的点,不会出现在 L i L_i Li
-
不变性:对于 L j L_j Lj中所有点, δ ( s , v ) \delta(s,v) δ(s,v)和 P ( v ) P(v) P(v)已经正确计算过了
-
基本情形(i=1): L 0 = { s } , δ ( s , s ) = 0 , P ( s ) = N o n e L_0=\{s\},\delta(s,s)=0,P(s)=None L0={s},δ(s,s)=0,P(s)=None
-
推断步骤:计算 L i L_i Li:
- L i − 1 L_{i-1} Li−1中每个顶点u
-每个顶点 v ∈ A d j ( u ) v\in Adj(u) v∈Adj(u)(v没有出现在 L j L_j Lj中,j<i)
-添加v到 L i L_i Li,设置 δ ( s , v ) = i , P ( v ) = u \delta(s,v)=i,P(v)=u δ(s,v)=i,P(v)=u
-
重复地计算 L j L_j Lj到 L i L_i Li(j<i),提升i直到 L i L_i Li是空集
-
对于 v ∈ V v\in V v∈V, δ ( s , v ) \delta(s,v) δ(s,v)没有被设置的点, δ ( s , v ) = ∞ \delta(s,v)=\infty δ(s,v)=∞
-
通过推断,广度优先查找正确地计算所有 δ ( s , v ) \delta(s,v) δ(s,v)和 P ( v ) P(v) P(v)
-
运行时间分析:
-
存储每个 L i L_i Li到数据结构中,需要 Θ ( ∣ L i ∣ ) \Theta(|L_i|) Θ(∣Li∣)迭代, O ( 1 ) \mathcal{O}(1) O(1)插入(比如动态数组和链表)
-
通过检查v是否在P中,来检查点v在不在 L j , j < i L_j,j<i Lj,j<i
-
维护 δ \delta δ和 P P P在集合数据结构中,支持字典操作耗时 O ( 1 ) \mathcal{O}(1) O(1)(直接访问数组或哈希表)
-
算法添加每个顶点u到level中,对每个 v ∈ A d j ( u ) v\in Adj(u) v∈Adj(u)花费 O ( 1 ) \mathcal{O}(1) O(1)
-
由handshake lemma得知,工作上边界: O ( 1 ) × ∑ u ∈ V d e g ( u ) = O ( ∣ E ∣ ) \mathcal{O}(1)\times \sum_{u\in V}deg(u)=\mathcal{O}(|E|) O(1)×∑u∈Vdeg(u)=O(∣E∣)
-
最后,花费 Θ ( ∣ V ∣ ) \Theta(|V|) Θ(∣V∣),为s不可达顶点 v ∈ V v\in V v∈V,赋值 δ ( s , v ) \delta(s,v) δ(s,v)
-
因此广度优先查找运行时间是线性的! O ( ∣ V ∣ + ∣ E ∣ ) \mathcal{O}(|V|+|E|) O(∣V∣+∣E∣)
-
-
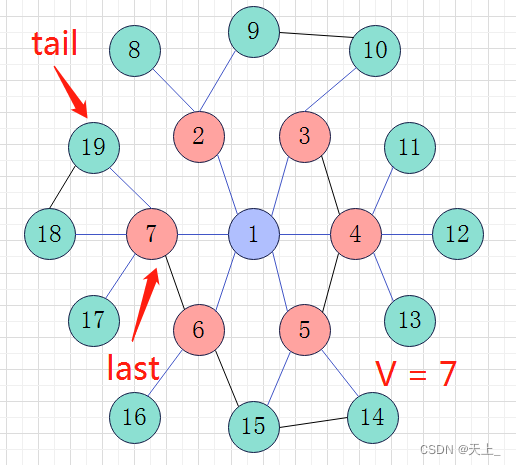
从例3图中点s出发,运行广度优先查找




](https://img-blog.csdnimg.cn/b091d34c87e74c39b3f8be09ad52c4e9.png)