目录

题目描述

算法思路

伪代码

总体算法

BFS算法

伪代码解读

BFS算法

图解

---

题目描述

六度空间理论的核心观点是，人类社交网络中的任何两个人之间，平均只需要通过不超过六个中间人（也就是六个社交关系）就可以建立联系。换句话说，你通过你认识的某个人，再通过他们认识的另一个人，以此类推，最终可以与世界上任何一个陌生人建立联系。

现假设给定了一个社交网络图，请对每个节点计算符合“六度空间”理论的节点占节点总数的百分比。

算法思路

对每个节点，进行广度优先搜索；

搜索过程中累计访问的节点数；

需要记录“层”数，仅计算6层以内的节点数。 

伪代码

总体算法

void SDS()
{
    for( each V in G )
    {
        count = BFS(V);
        Output(count/N);
    }
}

BFS算法

int BFS(Vertex V)
{
    visited[V] = true;
    count = 1;
    level = 0;
    last = V;
    Enqueue(V, Q);

    while (!IsEmpty(Q))
    {
        V = Dequeue(Q);
        for (每个邻接点W of V)
        {
            if (!visited[W])
            {
                visited[W] = true;
                Enqueue(W, Q);
                count++;
                tail = W;
            }
        }

        if (V == last)
        {
            level++;
            last = tail;
        }

        if (level == 6)
            break;
    }

    return count;
}

伪代码解读

BFS算法

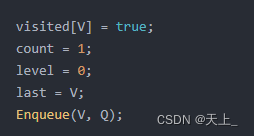
visited[V] = true; count = 1;

将起始节点 V 标记为已访问，并将计数器 count 初始化为 1。

level = 0; last = V;

初始化层级 level 为 0，最后一个节点 last 为起始节点 V。

Enqueue(V, Q);

将起始节点 V 入队，Q为队列，用于存储待访问的节点。

随后当队列不为空时进入while循环

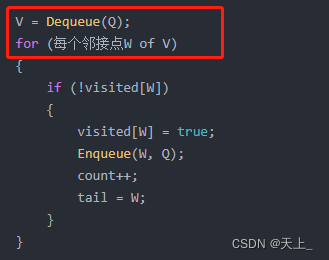
从队列中取出一个节点 V。

然后开始遍历节点 V 的每个邻接点 W，即与节点 V 相连的节点。

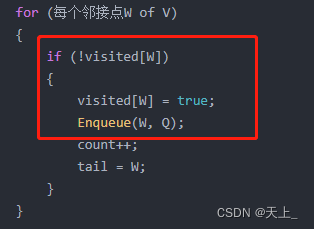
如果邻接点 W 没有被访问过，则执行以下操作：

• 将邻接点 W 标记为已访问。
• 将邻接点 W 入队。

 

增加计数器 count，表示访问的节点数量，并更新最后一个节点的位置为 W。 

 

 

如果当前节点 V 等于最后一个节点 last，表示完成了当前层的遍历。

所以就增加层级 level，并将最后一个节点更新为当前层的最后一个节点。

如果层级达到 6，即搜索到了六度空间的节点，跳出循环。

最后，返回从起始节点出发的路径上经过的节点数量。 

 

对于tail以及last的作用：

图解

最开始，last等于V：

然后对节点1进行出队列操作存在在V中，并将节点1的所有邻接点入队，对节点1的最后一个邻接点赋给tail：

 

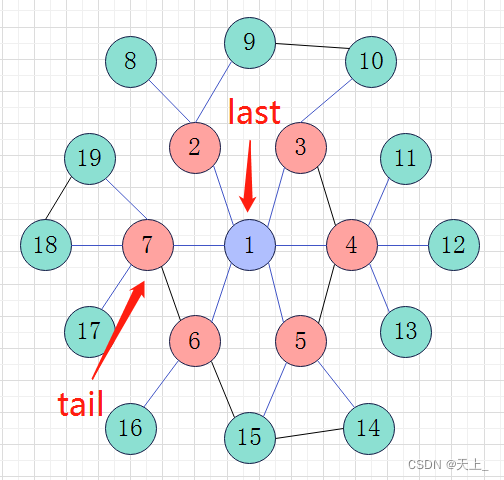
前面我们看到节点1已经出了队列，并被存储在V，判断V == last，如果相等，则表明已经遍历完一层了：

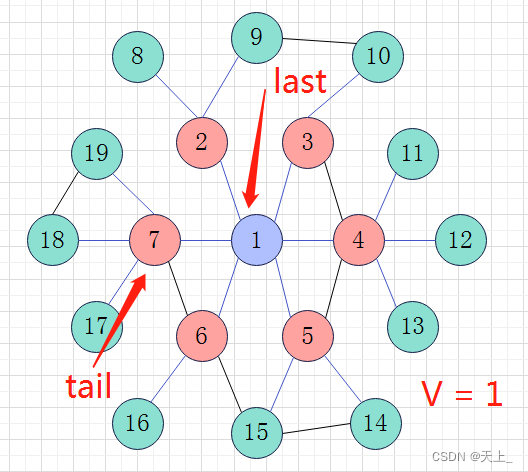
level++，把tail赋给last：

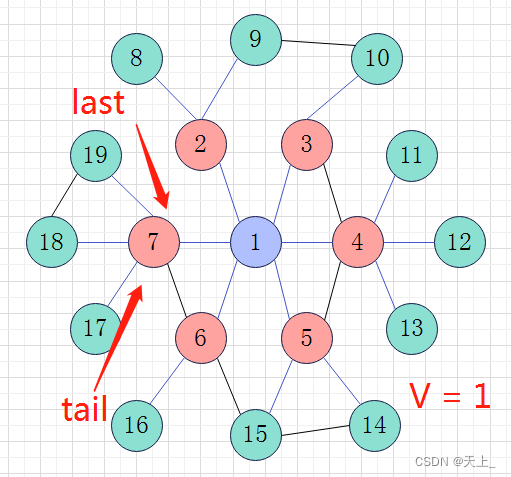
然后开始新一轮的循环，直到来到节点7，节点7的最后一个邻接点赋给tail，即节点19；此时last指向节点7；如此，通过last和tail来判断进入下一层。 

 

---

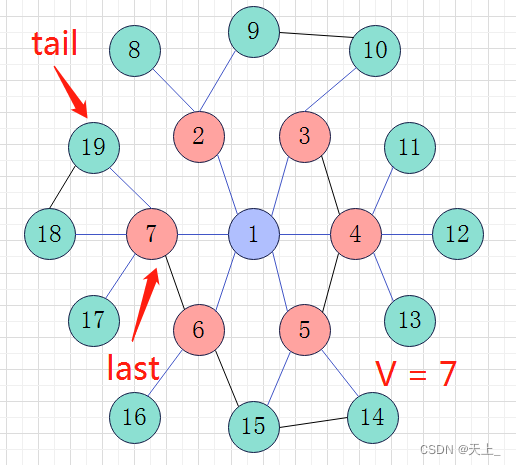
end

---

学习自：MOOC数据结构——陈越、何钦铭