分数 25

全屏浏览题目

作者 CHEN, Yue

单位 浙江大学

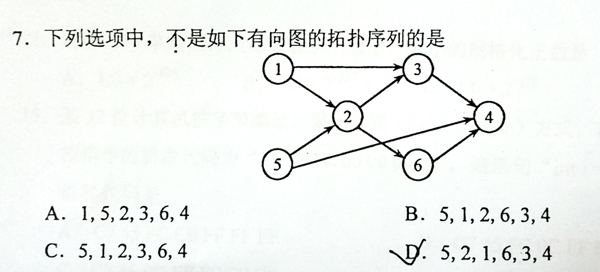
This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
6
5 2 3 6 4 1
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

0 4 5

鸣谢用户柳汀洲补充数据！

代码长度限制

16 KB

时间限制

200 ms

内存限制

64 MB

 算法思想：拓扑序列各相邻结点的顺序满足开始输入的边的端点顺序

举例如下：

判断序列5 2 3 6 4 1，序列下标分别为1 2 3 4 5 6，序列中1和2的下标分别为6和1不满足边的端点顺序故不是拓扑序列

#include<bits/stdc++.h>
using namespace std;
const int N=1009,M=10010;
int n,m;  
struct edge{
    int v1,v2;
}e[M];
int main(){
    cin>>n>>m;
    for(int i=0;i<m;i++)cin>>e[i].v1>>e[i].v2;//输入边 
    int k;
    cin>>k;
    int first=1;//用于第一次不是拓扑序列的输出 
    for(int i=0;i<k;i++){
        bool flag=true;
        vector<int>v;
        int pos[N];//记录询问序列各节点的位置 
        for(int j=0;j<n;j++){//询问序列各节点插入并记录位置 
            int t;
            cin>>t;
            v.push_back(t);
            pos[t]=j;
        }
        for(int j=0;j<n;j++){//该序列的结点先后位置若与边的端点先后顺序矛盾则不是拓扑序列 
            if(pos[e[j].v1]>pos[e[j].v2])flag=false;
        }
        if(!flag&&first)first=0,cout<<i;//第一次不是拓扑序列输出i 
        else if(!flag)cout<<' '<<i;//之后每次多输出个空格 
    }
    return 0;
}