1.22括号生成

参考：力扣题目链接；题解1，题解2

1.1.题目

在这里插入图片描述

1.2.题解

这道题目是使用递归的方法来求解，因为要求解所有的括号的可能情况，所以必须使用递归的方法来收集结果，而不能使用动态规划的方法。

做这道题目也可以大概理解什么时候要用回溯/动态规划的方法，就是要求所有的可能的时候，每个位置都有一种可能的选择，这个位置选了不同的结果，那么他也会影响后面的位置的选择。其实这个就是递归回溯算法来求解，或者动态规划来求解。

比如这道题使用递归回溯的方法来求解，其实就是一个树，当前节点选择不同的元素，得到的就是树中的不同节点。不同的当前节点决定了它后面展开的子树也是不同的。为了得到所有的可能，我们就要使用回溯：遍历完当前节点的所有子树之后，回溯算法回到当前节点的位置，然后重新选择当前节点选择的元素，从而得到其他的可能。

如下图所示，就展示了这个不同节点导致子树不同、以及回溯到当前位置得到其他的可能的过程。

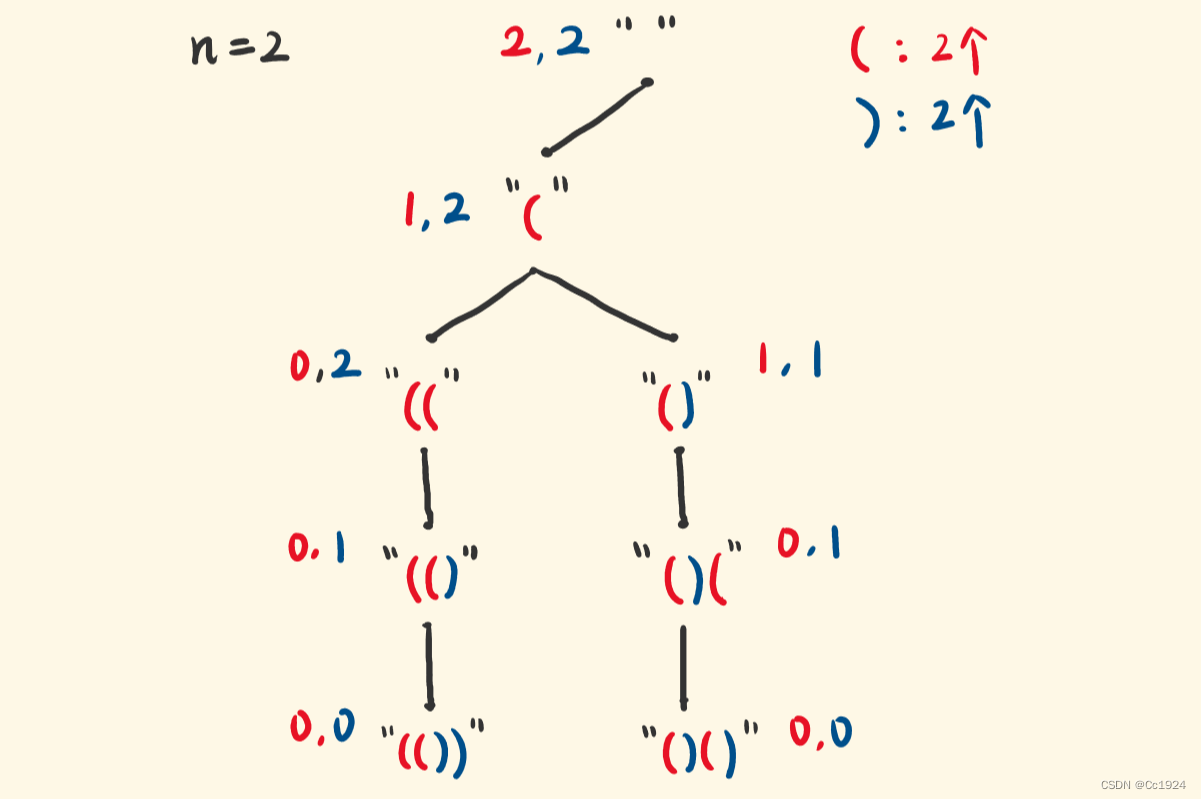
在这里插入图片描述
所以这道题目的题解如下：

首先要明白，一个合法的结果必须保证 ( 的个数 大于等于 ) 的个数。所以便利到当前位置的时候，可以有两个选择，即(或者)，但是有判断条件：

想选(：如果还有剩余的(，那么一定可以放(，因为它只需要等待后面有)来匹配它就行了，结果一定是合法的
想选)：如果还有剩余的)（实际上，由于我们都是优先选择(，并且保证(个数大于)的时候才会防止)，所以导致这个条件一定是满足的），并且当前传入的字符串中**(的个数大于)的个数**，那么就可以在当前位置加入)。

终止条件：当(和)个数都达到了个数n之后，就收集到了合法的结果，存储起来即可。

最后给出代码如下，和题解中不一样，而是沿用代码随想录中的写法，因为这种写法可以明显的显示出来回溯的过程，而题解的写法则是把这些内容忽略掉了。其实看下面的解答就可以发现，就是代码随想录中回溯算法那章的结果，非常简单。

vector<string> result;   // 最终收集的结果
string path;   // 当前收集的路径

void backtracking(int left, int right, int n)
{
    // 2.回溯终止条件：左右括号都收集满了
    if(left == n && right == n)
    {
        result.push_back(path);
        return;
    }

    // 3.开始递归和回溯
    // 3.1.还有剩余的(，那么(是可以无条件放的，都合法，只需要等待后面用)匹配它即可
    if(left < n)   
    {
        path.push_back('(');  // 加入一个(
        backtracking(left+1, right, n);   // 递归，选择后面的括号
        path.pop_back();   // 回溯，把上面加入的(弹出
    }
    // 3.2.还有剩余的), 并且当前已有的(个数 > 已有的)个数，那么可以加入)
    if(right < n && left > right)
    {
        path.push_back(')');   // 加入一个)
        backtracking(left, right+1, n);
        path.pop_back();   // 回溯，把上面加入的)弹出
    }
}

vector<string> generateParenthesis(int n)
{
    backtracking(0, 0, n);
    return result;
}

2.23合并K个升序链表

参考：力扣题目链接；参考题解

2.1.题目

在这里插入图片描述

2.2.解答

其实这道题目和昨天的合并两个升序链表思路基本是相同的，只不过由于有多个链表，所以代码中寻找当前位置的最小节点的时候需要一个for循环来判断所有的节点，从而寻找一个最小的节点。

另外最外面遍历链表到非空的大循环也不能使用两个链表都不是空来判断了，因为现在有多个链表，其中一个为空之后，其他的如果都不为空，那么都可以继续遍历，而不能直接退出。所以这里需要一个死循环，然后在循环里面判断当前选择的节点，如果当前没有选择到有效节点，说明所有的链表都是空了，则说明所有的链表都遍历完毕了，可以跳出循环了。

最后给出代码如下，其实还是很简单的，和昨天两个链表的题目差不多。

ListNode *mergeKLists(vector<ListNode *> &lists)
{
    int size = lists.size();  // 所有链表的个数
    ListNode* dummy = new ListNode(0);  // 新建结果链表，使用虚拟头指针
    ListNode* cur = dummy;

    while(true)
    {
        // 记录本次选择的最小节点的指针，和对应于vector中是哪条链表的节点
        ListNode* min_node = nullptr;
        int list_index = -1; 
        for(int i = 0; i < size; i++)
        {
            // 如果这条链表已经遍历到头了，那么不需要对比了
            if(lists[i] == nullptr)
                continue;
            // 运行到这里，说明这条链表还没有遍历完
            // 如果是第一次寻找当前位置的最小节点，则赋值min_node和list_index
            // 否则不是第一次，则如果当前节点值更小，则更新min_node和list_index
            if(min_node == nullptr || lists[i]->val < min_node->val)
            {
                min_node = lists[i];
                list_index = i;
            }
        }

        // 如果当期位置没有找到最小节点，说明所有链表都遍历完毕了，则直接跳出while循环
        if(min_node == nullptr)
            break;
        
        // 运行到这里，说明当前位置找到了最小节点，则先赋值、再后移节点
        cur->next = min_node;   // 赋值当前节点的下一个位置
        cur = cur->next;   // 移动当前节点到下一个位置
        lists[list_index] = lists[list_index]->next;  // 移动链表中的节点
    }

    ListNode* res = dummy->next;
    delete dummy;
    return res;
}