目录
1 排序基础
1.1 排序的基本概念
2 排序算法
2.1 插入排序
1.思想
2.实现
3.效率分析
4.优化
2.2 希尔排序
1.定义
2.实现
3.效率分析
3 交换排序
3.1 冒泡排序
1.定义
2.实现
3.效率分析
3.2 快速排序
1.算法思想
2.实现
3.效率分析
4 选择排序
4.1 简单选择排序
1.定义
2.实现
3.效率分析
4.2 堆排序
1.根堆
2.根堆建立
3.堆排序
4.效率分析
4.3 堆排序插入删除
1.插入
2.删除
5 其他排序算法
5.1 归并排序
1.原理
2.实现
3.效率分析
5.2 基数排序
1.定义
2.效率分析
3.适用领域
6 外部排序
6.1 外部排序
1.内外存数据交换
2.外部排序
3.时间分析
4.算法优化
6.2 败者树
1.算法思想
2.实现
6.3 置换-选择排序
6.4 最佳归并树
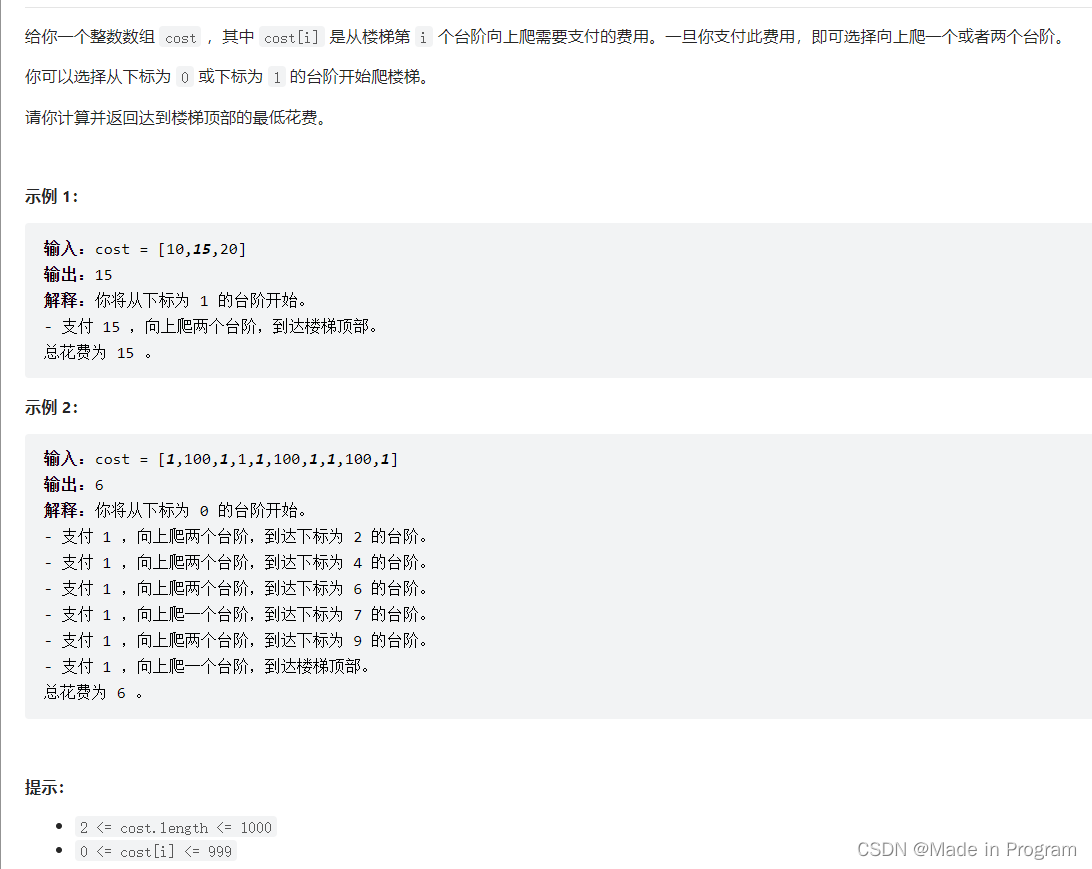
1 排序基础
1.1 排序的基本概念
排序:按关键字有序地排列表中的元素
评价指标:时间与空间复杂度、算法稳定性
分类:内部排序(数据在内存中)、外部排序
2 排序算法
2.1 插入排序
1.思想
算法思想:每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中,直到全部记录插入完成
2.实现
void Insertsort(int a[],int n)
{
int i,j = 0;
for (i = 0; i < n; i++) // 遍历整个数组
{
if (a[i] < a[i - 1]) // 若当前元素小于其前驱,进入下一层循环
{
int temp = a[i]; // 因当前元素应位于其前驱之前,先存放在临时变量中
for (j = i - 1; j >= 0 && a[j] > temp; --j) // 遍历该元素前驱之前的元素
{
a[j + 1] = a[j]; // 前驱依次后移
}
a[j+1] = temp; // 将该元素放在比他大的前驱前
}
}
}3.效率分析
空间复杂度O(1)
时间复杂度:O(n) ~ O(n^2)
平均时间复杂度:O(n^2)
稳定性:稳定
4.优化


2.2 希尔排序
1.定义
希尔排序︰先将待排序表分割成若干子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止。
2.实现

3.效率分析
空间复杂度:O(1)
最坏时间复杂度:O(n^2)
稳定性:不稳定
仅适用于顺序表
3 交换排序
3.1 冒泡排序
1.定义
从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即A[i-1]>A[i]),则交换它们,直到序列比较完。称这样过程为“一趟”冒泡排序。
2.实现

3.效率分析
空间复杂度:O(1)
时间复杂度:最好O(n),最坏O(n^2),平均O(n^2)
稳定性:稳定
适用于链表排序
3.2 快速排序
1.算法思想
在待排序表L[1..n]中任取一个元素pivot作为枢轴(或基准,通常取首元素),通过一趟排序将待排序表划分为独立的两部分L[1..k-1]和LIk+1..n],使得L1...k-1]中的所有元素小于pivot,Llk+1..n]中的所有元素大于等于pivot,则pivot放在了其最终位置L(k)上,这个过程称为一次“划分”。然后分别递归地对两个子表重复上述过程,直至每部分内只有一个元素或空为止,即所有元素放在了其最终位置上。
2.实现

3.效率分析


稳定性:不稳定
适用于链表排序
4 选择排序
4.1 简单选择排序
1.定义
每一趟在待排序元素中选取关键字最小的元素加入有序子序列
2.实现

3.效率分析
空间复杂度:O(1)
时间复杂度:O(n^210)
稳定性:不稳定
适用于链表
4.2 堆排序
1.根堆
若n个关键字序列L[ 1...n]满足下面某一条性质,则称为堆(Heap) :
若满足:L(i)≥L(2i)且L(i)≥L(2i+1) (1 ≤i sn/2) —―大根堆(大顶堆)
若满足:L(i)≤L(2i)且L(i)≤L(2i+1) (1 s i ≤n/2 ) —―小根堆(小顶堆)
将大(小)根堆看作顺序存储的完全二叉树,即根结点大(小)于左/右子树结点。
2.根堆建立
检查所有非终端结点(i <= [n/2])是否满足要求,若不满足将当前结点与更大的子树结点互换。

3.堆排序
每一轮都将堆顶元素加入有序子序列(与待排序中的最后一个元素交换),并将待排序元素序列再次调整为根堆。
基于大根堆得到递增序列

4.效率分析
若树高为h,某结点在第i层,则将这个结点向下调整最多只需要“下坠”h-i层,关键字对比次数不超过2(h-i)
时间复杂度:建堆O(n) + 堆排序O(n1og_2n) = O(n1og_2n)
空间复杂度:O(n)
稳定性:不稳定
4.3 堆排序插入删除
1.插入
以小根堆为例,新元素放入表尾,与父节点对比,若新元素较小就交换,持续上升。
2.删除
用堆底元素代替被删除的元素,并将该元素进行下坠交换。
5 其他排序算法
5.1 归并排序
将两个或多个有序序列合并
1.原理
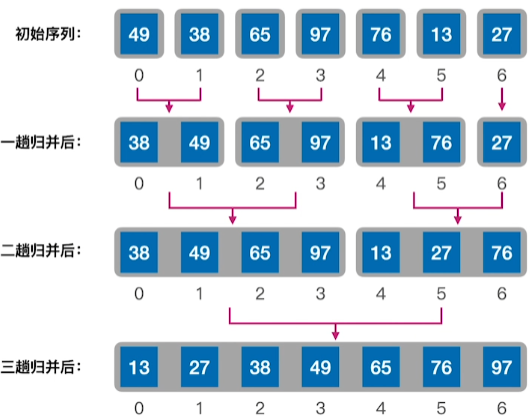
2.实现
将一个序列拆分成两个序列进行多轮归并排序

3.效率分析
时间复杂度:O(n*Log_2n)
空间复杂度:O(n)
5.2 基数排序
1.定义
第一轮以个位进行分配,将各元素链接后得到按个位递减排序的序列;次轮以十位进行分配,将各元素链接后得到按十位递减排序的序列;再次轮按百位进行分配,得到按百位递减排序的序列

2.效率分析
一轮分配O(n),一轮手机O(r),共d轮分配与收集
时间复杂度:O(d*(n + r))
空间复杂度:O(r)
稳定性:稳定
3.适用领域

6 外部排序
6.1 外部排序
1.内外存数据交换
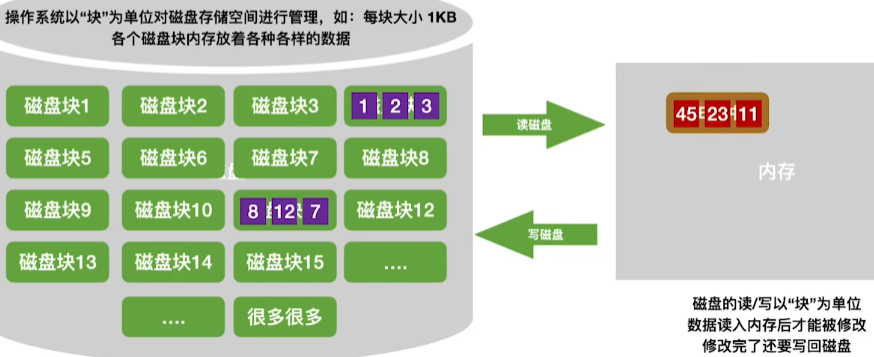
2.外部排序
因数据元素过多,外存数据无法全部读入内存进行排序,因此要进行基于归并排序的外部排序。
![]()
3.时间分析
外部排序时间开销=读写外存的时间+内部排序所需时间+内部归并所需时间
4.算法优化
可以使用多路归并,减少读写外存的时间。但内存开销与归并所需时间会增加
6.2 败者树
多路归并数增加,导致内部归并所需时间增加。
1.算法思想
可视为—棵完全二叉树(多了一个头头)。k个叶结点分别是当前参加比较的元素,非叶子结点用来记忆左右子树中的“失败者”,而让胜者往上继续进行比较,一直到根结点。
2.实现
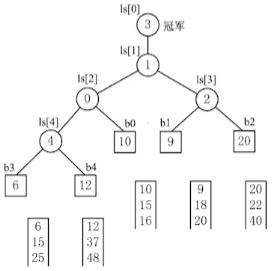
6.3 置换-选择排序

6.4 最佳归并树
要使磁盘I/O次数最少,就要让归并树的带权路径长度最小,构造K叉哈夫曼树。



![[附源码]计算机毕业设计病人跟踪治疗信息管理系统Springboot程序](https://img-blog.csdnimg.cn/e247eb823f544ee69daf2804d7919c8a.png)