前言

昨天无意中翻了翻以前的博文，发现关于强化学习部分的理论部分说的不是很清晰，属于那种懂得都懂，不懂的很难懂的那种。所以的话刚好趁期末有点空复习，那么把这个简要补充一下吧。从最基础的地方重新开始讲起吧，那么本文的话也是会将看起来比较复杂的概念进行简化，但是本文当中还是会有的，但是你可以选择性忽略，或者自行加一个补充。。

那么本文目标啥呢

1. 强化学习的概念
2. 强加学习的特征
3. 理解马尔科夫决策
4. bellman方程是啥
5. Q-learn
6. DQN

大概就是这5个目标吧，但是每一环节是环环相扣的，所以的话需要仔细观看本篇博文哈，OK，这也是难得写一次这种类型的基础的博文，略有不当，望多多指教。

强化学习概述

在开始疯狂输出前，我们需要好好理解一下到底啥是强化学习。这玩意到底是啥玩意，能够干啥。我们先来看一下这个玩意的官方一点的概念是啥吧：

强化学习（Reinforcement Learning,RL），又称再励学习、评价学习或增强学习，是机器学习的范式和方法论之一，用于描述和解决智能体（agent）在与环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题 。 强化学习的常见模型是标准的马尔可夫决策过程（Markov Decision Process,MDP）。按给定条件，强化学习可分为基于模式的强化学习（model-based RL）和无模式强化学习（model-free RL） ，以及主动强化学习（active RL）和被动强化学习（passive RL）。强化学习的变体包括逆向强化学习、阶层强化学习和部分可观测系统的强化学习。求解强化学习问题所使用的算法可分为策略搜索算法和值函数（value function）算法两类。深度学习模型可以在强化学习中得到使用，形成深度强化学习 。

这么说可能还是比较抽象，那么我们来提取一下关键词：再奖励，方法论，马尔科夫，最优化策略。

OK，这个的话就是我们整个强化学习的核心，没错就是这几个词，至于其他的，那是一种拓展。万变不离其中，因为强化学习是什么是一种方法论，这个就意味着他是一种思想，就比如web技术，具体的实现你可以使用java可以使用python可以使用go甚至是node.js（go和node.js这个基础的博文咱就不写了，鸽一下，别人写的比咱好，视频讲的都不错，GitHub也有很不错的教程）所以的话其他的什么算法都是实现强化学习的一种方案。

好接下来咱们再根据这几个关键词开始我们对强化学习的理解。

案例

我们现在来结合我们的比较出名的应用场景，案例，在结合我们的关键词来看看这个玩意现在用来干啥，为什么可以使用强化学习来做这个东西。

alphaGo

说到强化学习，这个玩意是比较有意思的一个案例，没记错的话应该是2016年的时候，那个时候我应该还在初中当英俊的少年。

无人驾驶

这个是咱们近期比较火热的一个话题，它的在这方面的应用非常的广泛。目前的话在咱们的生活当中用的比较多的是辅助驾驶，比如自动泊车，巡航之类的。

why

案例的话，我们就拿这几个就够了，总而言之，言而总之通过强化学习，我们可以让一个东西，具备一种类似于人类一样的决策思想，来完成某一种需要实时进行调整的任务。那么问题来了，凭什么强化学习可以做到这些事情，非她不可？！那么现在咱们来说说为啥。

首先我们回到一开始我们对于前面提取的关键词：再奖励，方法论，马尔科夫，最优化策略。

首先我们来解读解读啥是策略，策略就是一种步骤，一种执行的方案是吧，就比如我们下棋的时候一步一步下，一步一步怎么下，这个下的方法就是咱们的一种策略。那么我们下棋的时候肯定是期望我们能够找到最好的一种方案去做。并且每一次我们做了之后，都会得到一个及时的反馈，比如你下了一步，你的对手也会下一步给你进行一个及时反馈。那么同样的我们无人驾驶开车也是一样的，我们一步一步操作，保证车开的稳，又快又稳。

所以的话我们发现由于强化学习他可以做最优化策略，所以的话我们可以用这玩意来实现咱们的这种操作，当我们需要进行一些决策任务的时候，我们就可以选择强化学习方法来实现这个功能。

强化学习特点

ok，说完了前面强化学习的基本的一个概述之后，我想你对于强化学习应该有了基本的印象。并且我们现在可以对这个玩意儿下一简单的定义：这个东西是一个用于寻找到最优决策的一种优化方法论。并且为了实现这个方法论，我们衍生出了很多具体的算法用于实现她。

所以我们再给强化学习RL下一个定义，这玩意就是一个优化算法。只是优化的结果是我们的策略，是我们每一个步骤的操作，并且我们的操作是一次一次拿出来的。也就是和我们的其他算法，例如遗传算法其实是类似的，只是说我们的目标不太一样，怎么不一样呢遗传算法是求取具体的某一个函数的值或者是说我们的一个组合问题的结果。那么问题来了，强化学习的思路是怎么样的？有啥不太一样的嘛？

那么在这里的话，请记住我们目前找到的RL的特点，那就是：决策+最优化。

基本理论部分

首先我们来搞清楚强化学习到底是如何工作的。我们已经知道了她的特点那就是决策+最优化。那么我们这里就需要搞清楚两个问题，什么是决策，她这里的决策是指的啥，最优化如何最优化，最优化的是谁。搞清楚这个那么我们离搞清楚RL就不远了，那么在这里我们先来搞清楚决策。

刚刚我们拿下棋的例子说明了决策就是一步一步怎么个走法对吧。每一步怎么走的其实就是一个决策过程，那么这个就是决策，并且在我们下达决策之后，我们这边马上就可以得到外界给我们的一个反馈。例如你在此时选择向一个妹子表白，那么你很快就可以收到被拒绝的消息，得到一个反馈（这里不讨论成功的情况）。那么这个过程我们将如何表示呢。

ok,这里我们就可以对我们的决策进行一个简单的理解，决策就是在一个情况下做出一个行为，并且当行为做出之后，会得到一个及时的反馈，也就是会改变一个状态，比如你的心态，或者那个妹子的心态，总之会有一个状态的改变。例如你被拒绝了，于是你发奋图强，最终实现：“今日你对我爱答不理，明天我让你高攀不起”的一个目标。那么此时你的状态是有一个改变的。

基本概念

我们总是拿下棋，表白被拒这种案例来说明咱们这个高大上的概念实在是不妥，不符合我RL的规范。于是我们决定对我们刚刚的那些东西就行提出一些简单的概念。于是我们提取出了这些东西：

智能体

强化学习的本体，作为学习者或者决策者。也就是此时下棋的你

环境

强化学习智能体以外的一切，主要由状态集合组成。此时下棋的环境，比如我们下象棋有一系列的规程。

状态

一个表示环境的数据，状态集则是环境中所有可能的状态。

动作

智能体可以做出的动作，动作集则是智能体可以做出的所有动作。

奖励

智能体在执行一个动作后，获得的正/负反馈信号，奖励集则是智能体可以获得的所有反馈信息。例如下棋赢了之类的。

策略

强化学习是从环境状态到动作的映射学习，称该映射关系为策略。通俗的理解，即智能体如何选择动作的思考过程称为策略。

目标

智能体自动寻找在连续时间序列里的最优策略，而最优策略通常指最大化长期累积奖励。

因此，强化学习实际上是智能体在与环境进行交互的过程中，学会最佳决策序列。这个不就是咱们最优化的目标嘛

马尔可夫模型

那么刚刚的那个玩意如何用数学进行表示呢。我知道这个时候有人可能要问了，为什么要把那么痛苦的事情（举例中的表白失败）用数学来表示呢。原因很简单我们要做最优化问题，如果不能转为为数学模型，那么如何进行优化呀？！不懂得“反思”很难搞的呀。于是我们有这么一个玩意叫做马尔可夫模型来表示。

那么关于这个马尔科模型的，还有很多相关的概念，这里的话咱们就先不提了，我们只挑选我们需要理解的部分。毕竟博文不是专业图书，加上博主能力也有限，有些东西很难说清楚。

ok，好我们现在已经找到了一个模型，这个模型可以表示刚刚我们下棋，或者追女孩子被拒的一个情况。同样的，这个马尔可夫模型呢和俺们的强化学习类似，她也是一个大概念或者叫方法论吧。说不是人话就是：从模型的定义和性质来看，具有马尔可夫性质、并以随机过程为基础模型的随机过程/随机模型被统称为马尔可夫模型。其中包含马尔可夫链、马尔可夫决策过程、隐马尔可夫链（HMM）等随机过程/随机模型。

什么上来就放大招有那么一点带点不理会解是吧，没事咱们慢慢来，我们先来简单说说：马尔可夫链、马尔可夫决策过程，至于HMM，这个说清楚前面两个这个第三个就大概明白了是什么意思（老粉可能知道了，这玩意又可以被我水一篇博文出来了）还是那句话嘛，俺们重在理解，理解了去推倒数学公式不是有手就行。

马尔可夫链

（俄国数学家 Andrey Andreyevich Markov 研究并提出一个用数学方法就能解释自然变化的一般规律模型，被命名为马尔科夫链（Markov Chain）。马尔科夫链为状态空间中经过从一个状态到另一个状态的转换的随机过程，该过程要求具备“无记忆性 ”，即下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关。这种特定类型的“无记忆性 ”称作马尔可夫性质。马尔科夫链认为过去所有的信息都被保存在了现在的状态下了 。比如这样一串数列 1 - 2 - 3 - 4 - 5 - 6，在马尔科夫链看来，6 的状态只与 5 有关，与前面的其它过程无关。）

ok,我们先来说一下，那就是我们的马尔可夫链是什么东西，这里的话我们回到刚刚那个你被拒绝然后奋发图强的案例来（下棋的案例不好画图）

我们把时间先拉回到表白被拒绝的时间点：

于是你将迎来如下可能的状态的改变：
于是我们可以把这个状态的改变作为一个马尔可夫过程。那么链是啥呢，就是一系列状态的改变呀。

例如，你选择了图强，于是你选择去给博主来个三连，然后好好学习天天向上，最后达到人身巅峰。
状态由:s0-s1-s2-s3。因为我们刚刚在强化学习的时候也说过嘛，包括案例咱们都是连续的一个过程，比如开车，你总不可能方向盘拧一下就完事了吧。那么这个有一系列的状态的改变最终串联出来的一系列的状态过程就组成了一个链嘛。

我们在用形象一点的图来表示就是这样的：

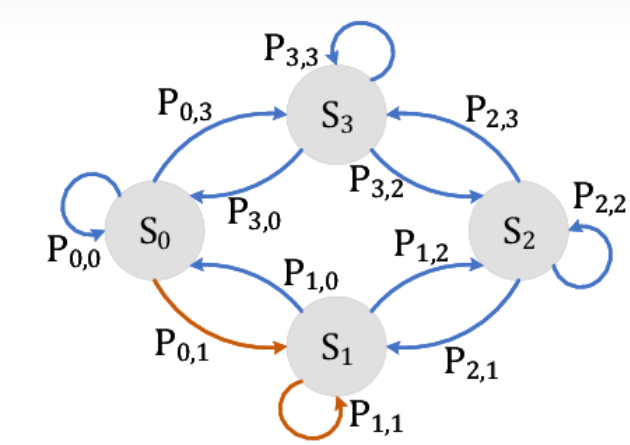
在这里我们简单解释一下这张图哈（没找到合适的图，又不好画只能先这样了）

S表示的就是咱们的一个状态，在刚刚的例子的话刚好就是有4个状态是吧。并且我们每一个时刻都只能有一种状态，总不能既堕落又图强吧，搁着叠加是吧。那么我们四个状态确定下来组成的序列，比如我们四个时间，每一个时间确定一个状态，并且我们的状态不重复，那么得到一个状态的过程例如 s1-s2-s3-s0 或者 s2-s3-s0-s1（假设这个的S的下标不是时间t，而是单纯表示状态的序号）那么这个组成的链状结构的话就是咱们的这个马尔科夫链。

P，说完了S，我们在来说说这个P是啥，这个P的话其实是咱们状态的转移矩阵，什么意思，当你此时决定图强的时候，下一个时刻还是不是图强是不一定的，例如某些人，阶段性奋发图强，持续性混吃等死。因此还有一个这个转移矩阵。

所以我们给出的那个图完整版是这样的：

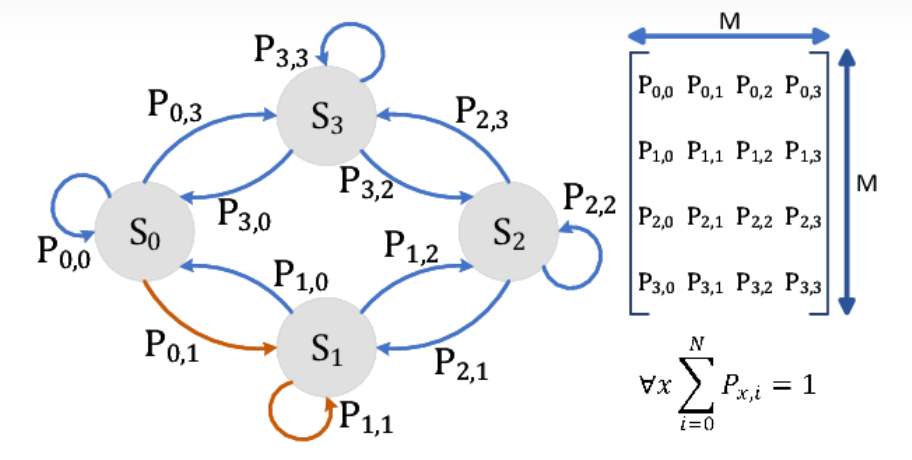
那么此时我想你对马尔科夫链应该是有一点了解了的。因为这玩意说白了其实就是算：由初始化状态通过N步骤之后达到最终状态的一个概率。

案例

OK，这里的话咱再举个例子吧，只需要使用到高中的数学只是即可。

我们有这样的一个状态和对应的一个状态转移的概率

现在我们求取从A开始两次之后还在A的概率。

通过高中的知识，我们可以这样算出结果：

P = 0.3 * 0.3 + 0.7 * 0.9 = 0.72
假设A—>A —>A
假设A—>B—>A
那么这个那两条链子就是马尔科夫链。好家伙，合着废了半天这个就是马尔科夫链呀，那问题来了我知道这个玩意有啥用呀。诶呀，咱们图强的目标是什么，是不是为了走上人身巅峰，我们知道每到一个阶段是不是说会得到一下东西，比如咱们好好学习，是不是可以变得优秀为以后打下基础，那么我们可以对自己简要的打个分对这个状态，当自己表现良好的时候，这样一来，当我们走向人身巅峰的时候，没有状态得到的评分之和都是非常高的。等等，这个不就是刚刚提到的这个嘛：

原来我们可以通过这个东西推算出来我们最后假设的每一种情况下能够得到的评分，假设评分可以换小钱钱，那么这个就是reward。

那么问题来了，是什么东西导致我们能够达到那个状态呢？！先前咱们是怎么说的，咱们是如何达到那个状态的来着？就是你为啥要决定奋发图强的来着的？哦，是因为你表白被拒绝了是吧（狗头）那么表白就是一种策略就是一种行为嘛。由于这冲动的行为导致了你将处于某一种状态。那么此时我们只是知道了表层。我们还需要知道你到底是为啥会做出这样的行为对吧。

马尔科夫决策过程

书接上回，我们还需要知道你为啥要做出这样的行为，并且我们还需要使用数学模型来表示你为啥要这样。之后我们就可以知道在这种情况下做出这个行为决策的原因，通过不断调整你的决策，最终让我们的马尔科夫链的奖励最大。那么这个做决策的过程就和我们正常思考的过程很像了。那么这个时候我们拿下棋的例子来举例子吧。老是那啥表白被拒被拒的太伤感了，搞得博主被拒过一样那么了解这个心太的变化（尽管是存在这种可能的）

来说点不是人话的东西：

所以一句话俺们通过上面的定义可以知道，其实就是加一点点细节，在我们状态转移的基础上加上决策。每次我们刚刚一直强调的案例，其实就是咱们的决策过程，就是你如何下棋，你如何表白并且被拒绝的一个过程。
前面介绍这个马尔科夫链只是为了咱们这个部分便于了解。

累计回报

OK，我们现在来试想一下，回到我们刚刚下棋的案例，我们现在知道了这几个东西：

1. 奖励
2. 状态
3. 反馈
4. 环境
5. 奖励

并且我们发现我们的状态，和反馈其实都是有环境进行反馈的。也就是说我们的环境包含了状态和反馈。那么反馈的是啥呢，我们要做最优化，那么反馈的应该是可以用来评判好坏的东西，并且我们不是不是一步到位需要一步一步慢慢来，因此每一步都需要有个东西来评价。那么这个东西是啥，显然就是前面提到的reward。

所以说，我们在下棋的时候，是不是可以这样，我们假设在当前的状态下，也就是在当前这一步，我们猜测一下如果下在这里会怎么，下在那里会怎么样，并且下在那里的时候我们给一个评估，那么也就是reward，那么这个时候你可能会说了，我选择当前能够得到最大的reward的地方然后把棋子放下去不就好了嘛。好像是可以，但是每一步最优一定是全局最优嘛？显示不一定吧，你下棋的时候也不可能只看这一步吧，而是看好几下，假设下到这里咋样，如果下到那里了后面又会咋样吧。

因此我们需要知道的不仅仅是我们下在那个地方之后能够得到的奖励吧，我们还要尽可能知道去预测后面能够的大的奖励吧。那么这个就是我们累计回报的意思。

那么公式就是这样的：

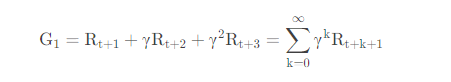
来咱们在这里简单解释一下这个函数是啥意思：
R，顾名思义就是咱们的奖励嘛，G就是咱们的累计回报嘛。那么接下来咱们再来解释一下下标是啥。
首先是咱们的t,这个是啥呢，这个其实就是time，时间。什么怎么还有一个时间，我们当前时刻假设为t,也就是此时此刻面对此情此景，要单走车取敌方首相的时候。那么数字是啥意思，这个那就是我现在走了这一步，那么我接下来可能会出现的状态能够得到的奖励呗。γ是啥，这个是咱们的一个因子，这样理解为了是不太确定的，因此权重比较低就是没有当下来的是在的意思，就是避免画大饼，我预测我走这里我能在10步之后赚100W，但是这个10步里面有太多变数了，因此要降低一下权重，避免“鬼迷心窍”。那么这个γ的取值也是0-1这个范围的。

在举个例子就是，在当前t时刻，我猜测接下来的状态转移是这样的（马尔科夫链）

我求出这个链路能得到的奖励就好了。

但是呢，记住一点就是，咱们这个都是预测，实际上需要实时的更新。大白话就是我猜的，不一定准。

所以说，在现在下棋的时候，我此时此刻，我有好几个位置可以落子，但是我需要选择累计回报最高的那个来落子。

概念及其求取流程

OK，又到了最OK的基础概念时刻了。现在我们来回顾一下，关于马尔科夫，强化学习，以及咱们先前提到的例子，我们现在已经扯到的东西。

首先是我们的一个概率转移矩阵是吧。这个转移矩阵就是咱们由状态1到状态2的一个概率。
之后是我们提到的马尔科夫链，这个和咱们的状态矩阵是一起的
然后是咱们提到的累计回报，我们的累计回报的表示方式呢刚刚那个公式
并且在当前的一个状态的时候，我们有很多选择，每一个选择对应一种行动，也就是对应一种策略。每一个策略的后果就是能够帮助我们转移到下一个状态。并且此时都对应一个奖励。
当我们选择下一个行动或者说策略的时候，我们通过累计回报来选择。

所以此时我们可以发现就是说，我们比较重要的是啥咧： 选择策略-那么如何选择-通过累计回报-累计回报怎么算呢。少年你问到点子上了！

其实这个咱们早就给出答案了。就是先前的那个算两次回到A那个位置的例子当中，我们说我们有一个马尔科夫链，并且知道状态转移矩阵，以及那个状态对应的reward。然后我们概率相乘做累加不就得到了一个累计奖励了嘛。

OK，现在我们来开始用数学语言来表达，但是我们先把我们先前一直提到的概念进行数学化表达；

策略：
强化学习的目标就是给定一个马尔可夫决策过程，去寻找最优的策略；
我们可以把策胳理解为在状态s下选择某一个动作的概率；
策略通常用符号来表示： 数学形式表示为：π(a|s)含义为；
策略π在每个状态s指定一个每个动作的发生概率；
如果策略π是确定的，那么策略π在每个状态下的每个动作的概率都是确定的。

然后我们再提取出一个概念叫做值函数。这个东西是啥呢。首先函数这个概念大家应该都知道输入一个值，得到另一个值。如果我们把刚刚得到的累计状态存储起来，以后你输入一个状态，我就把那个状态对应的累计回报给你那么，我们存储这个累计回报值的玩意，就是一个值函数。存放累计回报值的玩意的函数我们叫做“状态-值函数”
公式是这样的：

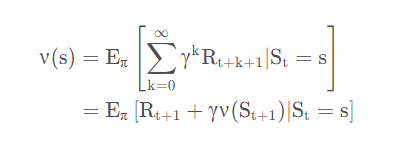
这个应该是很好理解的，如果概率论没有白学的话，看不懂，我们后面有个例子。

此外我们还有一个玩意叫做““状态-行为值函数””，这个是啥呢，就是在当前的这个状态下我做了一个动作能够得到的累计回报。因为在当前的状态的我们可以有很多个动作，上面那个值函数其实就是说把咱们的这个所有对应的动作的累计回报进行求和。那么这个函数的公式是这样的：

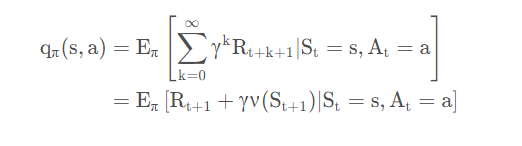
那么他们之间的关系呢就可以用下面的图表示：

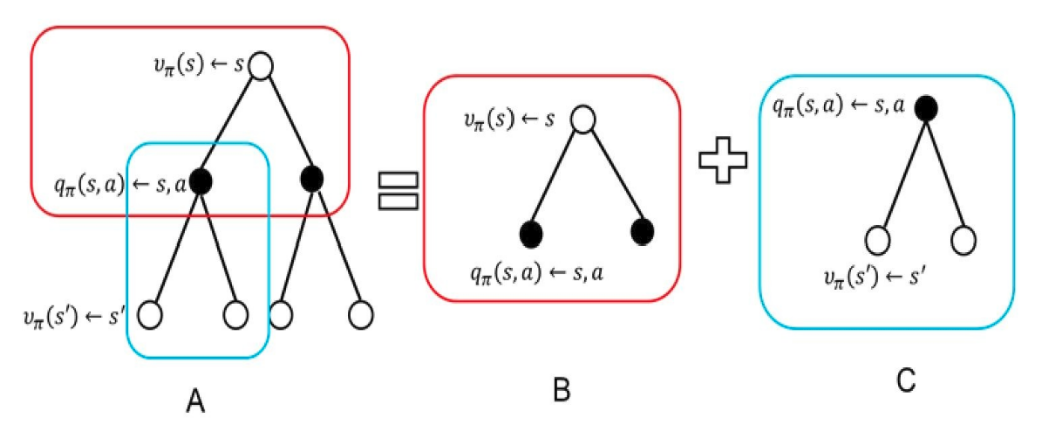
这个时候的话，我们在结合我们先前提到的状态转移概率，那么我们是不是就可以得到一个咱们对应的值函数。比如这个：

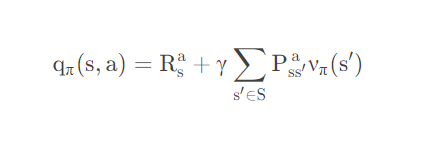
那么同样的这个“状态-值函数可以这样表示”

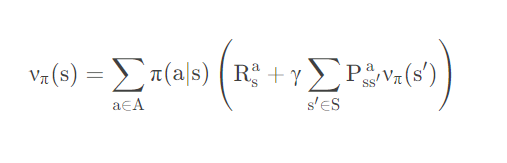
案例

OK，这个时候有点抽象，我们举个例子吧，我们举例子，这个例子是非常经典的例子。
来看到这个图：

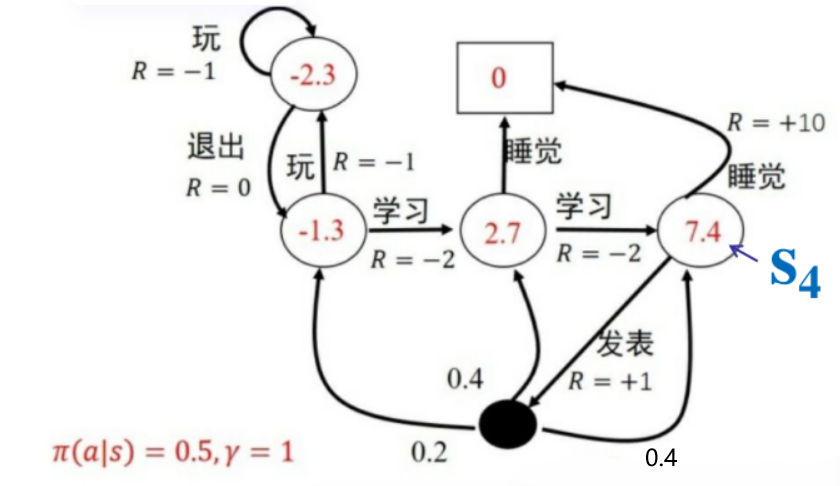
我们现在要对S4算一个累计回报，也就是咱们的“状态-值函数”V(s4) 的值

直接这样算：

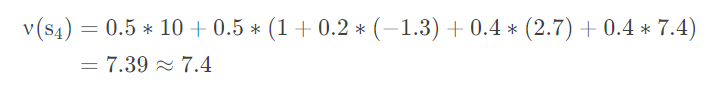
首先我们的在S4的时候我们有两个选择，睡觉和发表，概率都是0.5。如果选择睡觉那么一天结束，此时走入终点，也就是方框0，所以此时得到一个奖励就是0.5x10

之后的话是到发表这个节点，有0.5的概率，但是发表的话接下来有三个状态，结合上面的公式，我们只需要在算 0.2x-1.3+0.4x2.7+0.4x7.4 就可以了。

这个时候你可能需要问了，我们的公式是这样的：

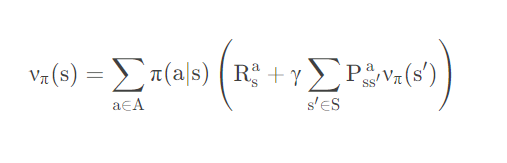
我们要算出一条链路的值呀，为什么案例只是算到0.2x-1.3+0.4x2.7+0.4x7.4就不算了，难道不应该继续算下去嘛，直到最终睡觉的一个情况嘛。OK，我们回到一开始对应马尔科夫的说明，他是当前状态之和上一个状态相关对吧。那么我们求取0.2x-1.3...这个值的时候我们是求取下一步的情况，我们的那个-1.3,2.7,7.4是怎么来的，这个东西是不是也是求取它的下一步的回报得到的，它的下一步的下一步也是通过下一步，下一步的下一步的下一步来的吧，那么我直接求下一步也就是那个式子是不是就是相当于直接把后面的一条链路直到最终状态都求到了，OK，这个就是看公式如果不看定义比较容易搞错的地方。

算法目的

OK，现在咱们已经知道了咱们的马尔科夫模型了。
我们知道了咱们的一些值函数，我们也知道了怎么求，我们可以通过这些值函数来决定我们的操作，最终改变一个状态实现一个目标。

因此我们不难发现，我们的强化学习算法其实目的就是：

但是别着急呀，我们操作的时候，我们其实按照这个

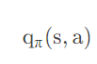
也就是咱们的“状态-行为值函数”就可以去决定我们的一个策略，我们选择最大的就好了嘛。但是这个玩意咱们一开始是压根就不知道的呀。只有我们不断去尝试才能够去知道的呀，不断试探才能知道底线嘛（狗头）但是只要我们能够得到或者求取出这个玩意，我们就可以无敌了，我们只需要不断去尝试就好了，因为我们又不是量子一次性就可以知道每一个动作能够得到的累计回报，我们只能知道当前的，那么我们就可以通过直接尝试，结合咱们的当前的奖励去不断尝试猜测，最后越来越准就好了。

Q-Leaning

OK，现在我们的问题定位到如何找到这个Q（s,a）函数。那么我们的Q-Learning就诞生了。我们首先直接看到伪代码。

我们直接看到我们那个公式的更新方程，这个和咱们那个求取V(s4）求取V(s4|发表)的过程有那么一点相似，但是还多了一点东西好像认不出来。OK我们来好好解读一下。

真实值与预测值

其实咱们前面一直在强调，那就是咱们的这些值函数，其实都是一个预测，通过马可夫模型进行预测的，我们通过预测的这些值来达到我们最优的一个策略。只有我们尽可能保证我们预测的“状态-行为值函数”更加准确我们才有可能更好地得到咱们的这个策略，也就是，咱们的这个Q（s,a）相当于一份棋谱，这玩意都不准，棋怎么可能可以下好呢。所以为了能够让我们的这个准一点，我们搞出真实值和预测值这样的概念，那么这个值是啥呢，显然就是对应的累计回报嘛。

但是问题来了，预测值我们知道呀，预测嘛，尝试呗，但是你说，真实值我上哪知道去？每次我们确实是不知道的，但是我们可以知道的就是随着我们不断尝试，我们的预测应该是越来越准的，因为我们把更多的可能性给走出来了，并且我们可以知道，结合公式一开始咱们提到的这个公式:

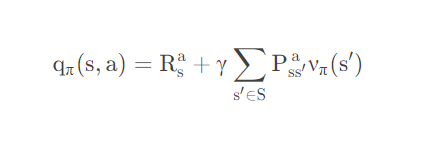
我们其实也是可以知道的，那就是我们最后的话这个对应的值应该是不断变大的。所以说我们直接一点，那就是我们我们更新Q（s,a)的时候直接按照某一种规则变大就好了。那么问题来了，为什么不直接按照上面的公式更新呢？V(s) 咱来的？Q(s,a1)+Q(s,a2)+…Q(s,an)来的，本来一个就不准，现在来一堆是不是更不准了。尽快能减少依赖吧。

那么真实和预测分别表示啥呢，就是这个：

案例

ok，又到了咱们的案例部分了，这里的话咱们举一个（以前的例子）我们让我们的强化学习Q算法来玩一个游戏，规则是这样的：

我们具象化我们的Q（s,a）是这样的：

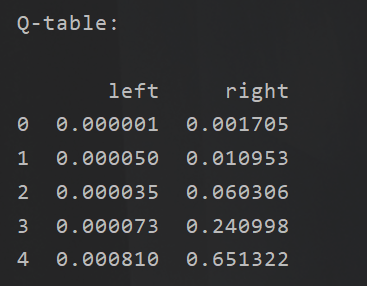
首先在回顾一下我们最开始提到的概念：

智能体

强化学习的本体，作为学习者或者决策者。也就是此时下棋的你

环境

强化学习智能体以外的一切，主要由状态集合组成。此时下棋的环境，比如我们下象棋有一系列的规程。

状态

一个表示环境的数据，状态集则是环境中所有可能的状态。

动作

智能体可以做出的动作，动作集则是智能体可以做出的所有动作。

奖励

智能体在执行一个动作后，获得的正/负反馈信号，奖励集则是智能体可以获得的所有反馈信息。例如下棋赢了之类的。

策略

强化学习是从环境状态到动作的映射学习，称该映射关系为策略。通俗的理解，即智能体如何选择动作的思考过程称为策略。

目标

智能体自动寻找在连续时间序列里的最优策略，而最优策略通常指最大化长期累积奖励。

因此，强化学习实际上是智能体在与环境进行交互的过程中，学会最佳决策序列。这个不就是咱们最优化的目标嘛

现在目标是走到重点，智能体是小人。此外我们还有对应的环境，那么这个环境其实就是我们制定的游戏。我们还要编写出这个游戏。

这部分的话我们直接看到代码就好了都有注释哈：

import numpy as np
import pandas as pd
import time

np.random.seed(2) 
#作用和pytorch的那个一样


N_STATES = 6
ACTIONS = ['left','right']
EPSILON = 0.9 #greedy
ALPHA = 0.1 #学习速率
GAMMER = 0.9
ECPHOS = 10 #轮数
FRESH_TIME = 0.01 #演示效果用的


def Init(n_states,actions):
    #初始化
    table = pd.DataFrame(
        np.zeros((n_states-1,len(actions))),
        columns=actions
    )
    return table


def ChoseAction(state:int,QTable:pd.DataFrame):
    state_actions = QTable.iloc[state,:]
    # 大于0.9 也就是0.1部分随便选择
    gailv = np.random.uniform()
    if(gailv>EPSILON or state_actions.all(0)==0):
        action = np.random.choice(ACTIONS)
    else:
        action = state_actions.idxmax()
    return action

def GetReward(S,A):
    #我觉得这个有点类似与一个损失函数，只是这个损失函数很特殊
    #这个是模拟游戏环境，同时也是假设如果我选择了a1 我会得到的R和下一步对应的步数是几
    if (A=="right"):
        if(S==N_STATES-2):
            #我们是假设往右走的
            S_= 'win'
            R = 1
        else:
            S_ = S+1
            R = 0
    else:
        R = 0
        if S==0:
            S_ = S
        else:
            S_ = S-1
    return S_,R

def updateEnvShow(S,ecpho,step_counter):
    #在终端可视化显示行走的过程
    env_list = ['-'] * (N_STATES-1) +['F']
    if(S=='win'):
        interaction = "当前训练轮数 %s: 胜利时走的步数= %s "%(ecpho+1,step_counter)
        print("\r{}".format(interaction),end="")
        time.sleep(2)
        print("\r",end="")
    else:
        env_list[S]='o'
        interaction=".".join(env_list)
        print("\r{}".format(interaction),end='')
        time.sleep(FRESH_TIME)


def QLearning():
    QTable = Init(N_STATES, ACTIONS)  
    for ecpho in range(ECPHOS): 
        step_counter = 0
        S = 0
        # 是否回合结束
        isWin = False
        updateEnvShow(S, ecpho, step_counter)
        while not isWin:

            #选择行为
            A = ChoseAction(S, QTable)
            # 得到当前行为会得到的Reward，以及下一步的情况
            S_, R = GetReward(S, A)
            # 估算的(状态-行为)值
            q_predict = QTable.loc[S, A]
            if S_ != 'win':

                # 实际的(状态-行为)值 这个就是类似与G1
                q_target = R + GAMMER * QTable.iloc[S_, :].max()

            else:
                #  实际的(状态-行为)值 (回合结束)
                q_target = R
                isWin = True    

            QTable.loc[S, A] += ALPHA * (q_target - q_predict)  #  QTable 更新
            S = S_  # 探索者移动到下一个 state
            # 环境更新显示
            updateEnvShow(S, ecpho, step_counter+1)

            step_counter += 1
    return QTable
if __name__ == '__main__':
    QTable = QLearning()
    print("\r\nQ-table:\n")
    print(QTable)

代码还是非常简单的。公式的实现咱们也有哈。

离线学习Sarsa

之后的话我们在刚刚的话我们还注意到一点，那就是咱们这个：

这个是啥：off-policy 什么玩意在线学习的意思，那么有在线的是不是就有离线的，显然是的，有男的怎么会没有女的。那么这个玩意是啥呢，有个算法和咱们的Q-Learning类似的，叫做Sarsa

这个算法其实和QLearning很像

区别在哪，或者说为什么要有这个算法咧？

选择动作函数

其实区别就在于选择下一步的策略。
我们可以重点看到这个函数：

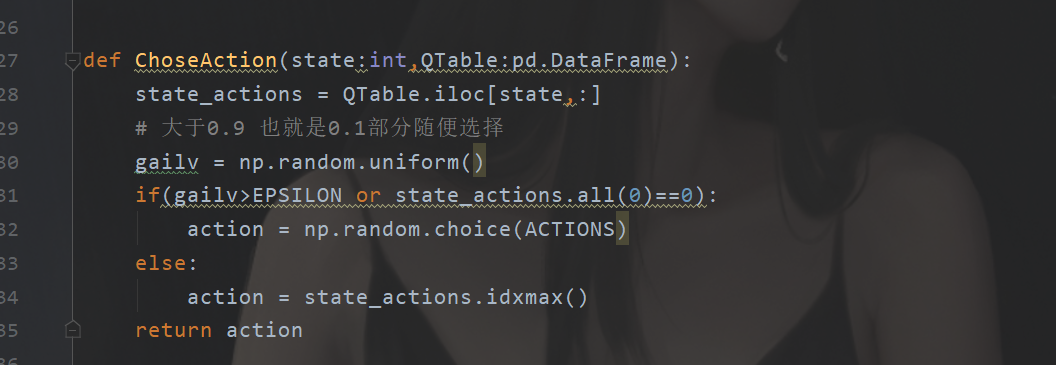
我们返回的动作有一定概率不是奖励最大的动作。

对于QLearning来说，他每一次都会现在新的动作，也就是每一次都有概率不是选择最优的动作。

但是Sarsa不是呀，它下一个动作就是选择下一步当中奖励最大的。

换一句话说QLearning 胆子大，Sarsa保守。有着不同的收敛性，相对而言QL会想着找到更好的路，Sarsa比较保守，走“稳路”。

代码

代码也是类似的，只需要修改一个函数

def SARSA():
    QTable = Init(N_STATES, ACTIONS)
    for ecpho in range(ECPHOS):
        step_counter = 0
        S = 0
        # 是否回合结束
        isWin = False
        updateEnvShow(S, ecpho, step_counter)
        A = ChoseAction(S, QTable)  # 先初始化选择行为
        while not isWin:

            S_, R = GetReward(S, A)
            try:
                A_ = ChoseAction(S_, QTable)
            except:
                # 这里说明已经到了终点（如果报错）
                pass
            q_predict = QTable.loc[S, A]
            if S_ != 'win':
                q_target = R + GAMMER * QTable.iloc[S_, :].max()

            else:
                q_target = R
                isWin = True

            QTable.loc[S, A] += ALPHA * (q_target - q_predict)  #  QTable 更新

            S = S_  
            A = A_  
            updateEnvShow(S, ecpho, step_counter+1)

            step_counter += 1
    return QTable

DQN

前面咱们说了这个Q-Leaning，我们已经知道了基本的一个强化学习算法了，但是呢，这个玩意是不是无敌了？OK，我们现在还是下棋，我们说，我们这个Q（s,a）是棋谱对吧，但是呢，就比如咱们下围棋吧，这个可能是很多的呀，我们不可能也很难直接把全部的S和 A都存进去吧，存进去了也很难检索呀，数据量很大呀。

所以有什么方式能够优化呢。
我们原来说 Q（s,a) 是什么东西，是一个“状态-行为值函数”

是一个函数呀，既然如此，我为什么不能去直接使用一种函数呢，你只需要输入当前的State然后我就能告诉你对应的action 的值

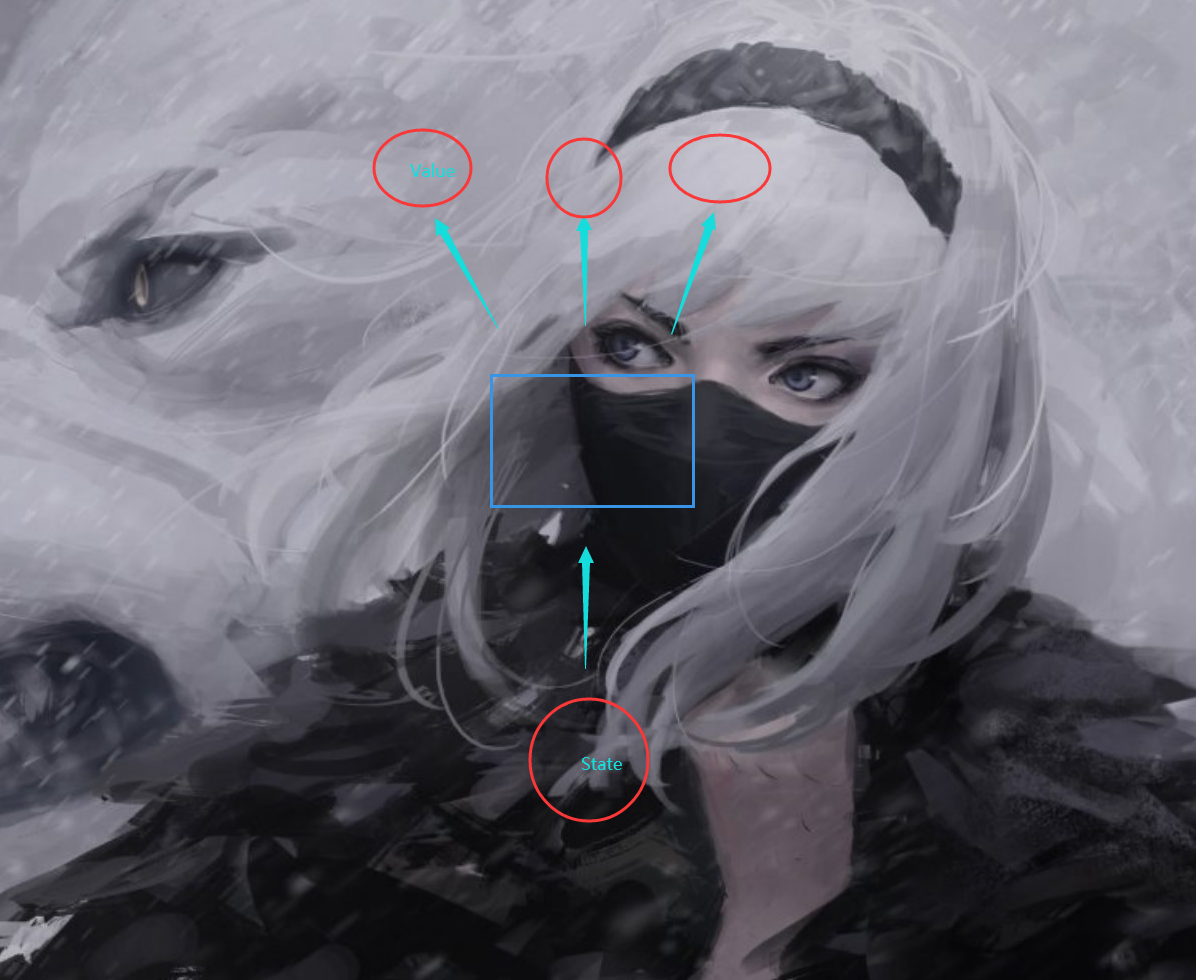
那么我们怎么才能找到这样的函数呀？
什么东西能够达到这样的效果咧？

当然是神经网络呀！这玩意不是可以“拟合”出任何我想要的函数嘛！！！
于是我们使用神经网络来代替了我们的Q表

流程

此时我们的流程也发生了变化。
这里的话我们是有两个版本的一个是2013年的

还有一个是现在使用的2015年的

这里多引入了一个记忆库的玩意，原因是为了打破原来数据之间的连贯性，也就是数据之间的强相关性。

原来我们的数据和上一步或者上几步之间是紧密相连的，换一句话来说，对于相邻的数据之间的相关性较高，这个就会导致一个问题，例如我们在做拟合的时候，就会导致局部拟合效果很好但是全局效果差，也就是两个图像部分贴合但是整体贴合度差。（还好老子玩过数学建模）

所以为了降低这玩意，这里选择了存储一定步骤的数据，然后随机选择一部分，然后去训练，你拟合，这样就可以降低训练数据之间的相关性。

你可以这样理解。如果我的输入是连续的，不是打乱的，此时我在做拟合，那么，为了拟合当前的这一端，我可能就会破坏另一端，最后当我拟合完毕后，可能只有一端是贴合的。现在我数据大散，那么我的拟合的点在图像上是均匀的，那么总体上贴合就会比较好。

那么流程如下：

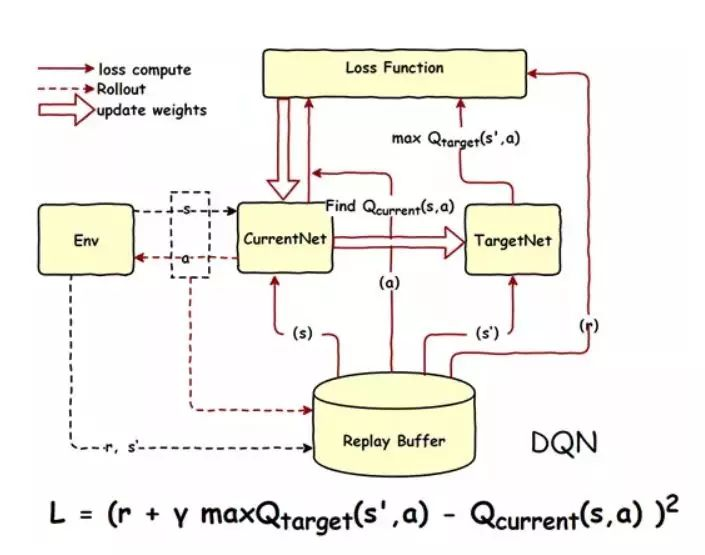
预估“表”与实际“表”

此外还有一个细节。在我们原来的时候

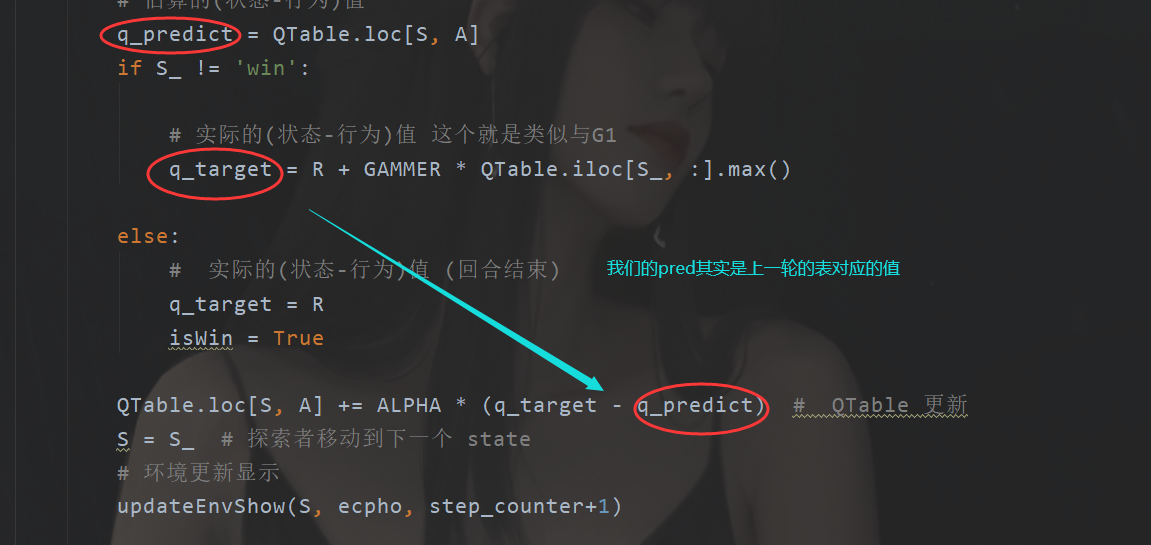
但是现在的话，由于我们是直接使用了这种“函数”所以我们可以单独使用两个神经网络去分别代表实际和估计（预测）

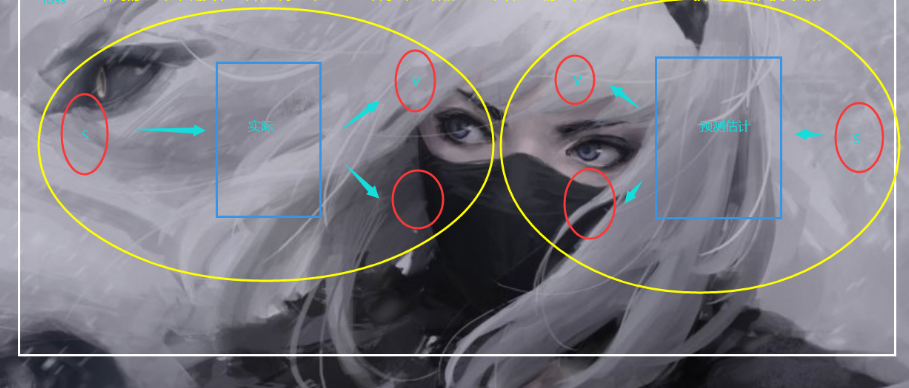
而我们的损失函数也很巧妙，什么时候我们会有最优解，显然最明显的特征是，我们的系统趋于稳定。
于是：

编码

坑点

在开始之前先来说说我踩到的坑。
第一个：

对于二维张量来说，max(a,1)是取行的最大值，因为我们这里的action是1x2的，要按照行来，但是一维的张量不行，于是只能取0

第二个：

是我们构建神经网络的坑，我原来使用的是ReLu()也就是nn下面的，但是报错，有毛病，后来我又试了一些Function下面的relu，结果ok了，得到了我想要的输出维度。

环境修改

现在俺们仿造一下gym，我们自己把刚刚的那个“走棋” 给做成环境出来。

我们封装一下：

import time

"""
这个环境是这样的，
每一步的observer只有一个，
到重点一共是5步,往右走一共6个格子，所以终点的下标是4
"""

class Env(object):

    def __init__(self):

        self.N_STATES = 6
        self.Actions = ['left','right']
        self.FRESH_TIME = 0.001
        self.Win = 'win'

    def updateEnvShow(self,S, ecpho, step_counter):
        # 在终端可视化显示行走的过程
        env_list = ['-'] * (self.N_STATES - 1) + ['F']
        if (S == self.Win):
            interaction = "当前训练轮数 %s: 胜利时走的步数= %s " % (ecpho + 1, step_counter)
            print("\r{}".format(interaction), end="")
            time.sleep(2)
            print("\r", end="")
        else:

            env_list[S] = 'o'
            interaction = ".".join(env_list)
            print("\r{ins}:当前训练轮数：{ec},当前步数{st}".format(ins=interaction,ec=ecpho+1,st=step_counter),end="")
            time.sleep(self.FRESH_TIME)

    def getStatus(self):
        return 1

    def getActions(self):
        return self.Actions

    def GetReward(self,S, A):
        # 我觉得这个有点类似与一个损失函数，只是这个损失函数很特殊
        # 这个是模拟游戏环境，同时也是假设如果我选择了a1 我会得到的R和下一步对应的步数是几

        if (A == 1):
            if (S ==  - 2):
                # 我们是假设往右走的
                S_ = self.Win
                R = 1
            else:
                S_ = S + 1
                R = 0
        else:
            R = 0
            if S == 0:
                S_ = S
            else:
                S_ = S - 1
        return S_, R
    def reset(self):
        #开始
        self.updateEnvShow(0,0,0)
        return 0

运行代码

现在我们开始进行完整的编码

import torch
from torch.nn import *
from torch import nn
from DQNNetWork.Env import Env
import numpy as np
import torch.nn.functional as F

#初始化运行环境
env = Env()

N_Status= env.getStatus()
HIDDEN_NUMBERS = 5
ACTIONS = env.getActions()
ACTIONSLEN = len(ACTIONS)
MEMORY_CAPACITY = 30
LR = 0.01
EPSILON = 0.9
BATCH_SIZE = 2
TARGET_REPLACE_ITER = 10
GAMMA = 0.9
ECPHOS = 50
class NetWork(nn.Module):
    #代替表格Q的神经网络
    def __init__(self, ):
        super(NetWork, self).__init__()
        self.fc1 = nn.Linear(N_Status, 50)
        self.fc1.weight.data.normal_(0, 0.1)   # initialization
        self.out = nn.Linear(50, ACTIONSLEN)
        self.out.weight.data.normal_(0, 0.1)   # initialization

    def forward(self, x):
        x = self.fc1(x)
        x = F.relu(x)
        actions_value = self.out(x)
        return actions_value


class DQN(object):
    def __init__(self):

        #在我们使用表格的时候，我们需要的是一个现实计算的V，和一个估计的
        #然而实际上我们做的时候其实只是把上一轮的作为预估的表然后更新下一轮
        #那么现在我们直接使用两个神经网络一个就是实际的“表”一个是预估的表
        #还有一个好处，原来用一个表是预估和实际的步长只有1，现在我可以随意设置
        #于是这个过程就变成了两个网络相互学习的过程
        self.eval_net, self.target_net = NetWork(), NetWork()

        self.LearnStepCount = 0
        self.MemoryCount = 0                                         # 记录了几条记忆
        self.Memory= np.zeros((MEMORY_CAPACITY, N_Status * 2 + 2))     # 初始化记忆
        self.optimizer = torch.optim.Adam(self.eval_net.parameters(), lr=LR)
        self.loss_func = nn.MSELoss()


    #我们的Status是只有一个状态的
    def ChooseAction(self,s):
        s = torch.FloatTensor([s])

        if np.random.uniform() < EPSILON:  # greedy
            actions_value = self.eval_net.forward(s)
            #由于我们是1x2的所以我们是0
            action = torch.max(actions_value, 0)[1].data.numpy()
            #选择出我们value最大对应的下标0，1
        else:
            action = np.random.randint(0, ACTIONSLEN)
        return action

    def Remember(self, s, a, r, s_):
        #这个是我们的记忆体
        transition = np.hstack((s, [a, r], s_))
        index = self.MemoryCount % MEMORY_CAPACITY
        self.Memory[index, :] = transition
        self.MemoryCount += 1

    def Learn(self):
        # 达到一定的训练步数后，我们更新我们的target网络
        #我们的这个函数的目的只有一个得到俺们的Q表，Q神经网络
        if self.LearnStepCount % TARGET_REPLACE_ITER == 0:
            self.target_net.load_state_dict(self.eval_net.state_dict())
        self.LearnStepCount += 1

        # sample batch transitions
        SelectMemory = np.random.choice(MEMORY_CAPACITY, BATCH_SIZE)
        selectM = self.Memory[SelectMemory, :]
        S_s = torch.FloatTensor(selectM[:, :N_Status])
        S_a = torch.LongTensor(selectM[:, N_Status:N_Status+1].astype(int))
        S_r = torch.FloatTensor(selectM[:, N_Status+1:N_Status+2])
        S_s_ = torch.FloatTensor(selectM[:, -N_Status:])

        #这一步得到了我们一个batch_size的最佳值（最佳）
        q_eval = self.eval_net(S_s)
        q_eval = q_eval.gather(1, S_a)
        #这个是下一步动作对应的值
        q_next = self.target_net(S_s_).detach()
        #更新我们的G
        # shape (batch, 1)
        q_target = S_r + GAMMA * q_next.max(1)[0].view(BATCH_SIZE, 1)
        loss = self.loss_func(q_eval, q_target)

        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()




if __name__ == '__main__':
    Dqn = DQN()
    for ecpho in range(ECPHOS):

        s = env.reset()
        e_step = 0
        isWin = False
        while not isWin:
            if(s >=env.N_STATES-2):
                env.updateEnvShow(s, ecpho, e_step)
                isWin = True
                print("")
            env.updateEnvShow(s,ecpho,e_step)

            a = Dqn.ChooseAction(s)
            s_,r = env.GetReward(s,a)
            Dqn.Remember(s,a,r,s_)
            #更新我们的Q表，准确来说是我们的Q神经网络
            #但是我们不是立即更新，我们先随便试一下，然后从里面去寻找最优值
            if(Dqn.MemoryCount>MEMORY_CAPACITY):
                Dqn.Learn()
            e_step+=1
            s=s_

运行效果

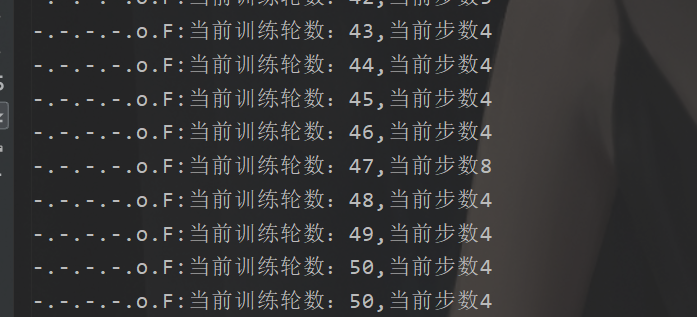
这里注意一下的是，我的那个步数是从0开始的，所以应该是走了5步，也刚好是要走5步到终点的。

总结

又水了一篇博文~