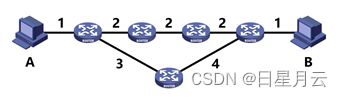
概念解释

先说明几个概念（非严谨定义）

码字：一个包含了数据位和校验位的n位单元，也就是“一种”编码

编码：由码字组成的可以表达传递信息的集合，这里不是指编码的过程，而是一个名词。一个编码就是一套系统，包含所有编码所能组成的码字

海明距离：两个码字中不同位的个数，即两个码字中不同“字符”的差异总数

偶校验：在原有的码字上添加一位，使得包含了该校验位的码字所有的“1”的总数为偶数

二进制拆分：所有整数总可以拆分为2的幂的和

块编码的检错和纠错特性取决于它的海明距离。为了可靠的检测d个错误，需要一个海明距离为d+1的编码。——《特南鲍姆，计算机网络第6版》

 在刚接触这句话，我很难理解其含义。为何需要使用一个编码来检测错误？这就需要弄清楚此处编码的概念。事实上，这里的一个编码，不是指的编码的实例化即一个码字，而是这套编码（系统）中相邻两个码字的最短海明距离是d+1

之所以产生了错误，是因为出现了不可能(invalid)编码，该编码在这套编码体系中不存在！由于相邻码字之间海明距离为n，即有n位差异，当发生了错误的编码与这套编码中任意一个与之相邻的编码计算海明距离时，只有n-1种错误的可能，这是两个相邻处于该编码系统中合法码字中间的不合法码字

要检测n位错误，而如果这个编码系统中相邻码字的海明距离为n的话，这个发生了n位错误的编码就会被当作合法的相邻码字处理，无法检测出错误。海明距离小于n同样的道理。这个问题的核心在于是否会产生不合法的码字

纠错理论

要求的最小码距

• 检测(detect)m个(bit的）错误：m+1
• 纠正(correct)n个错误:2n+1（向接近的码字纠正）
• 检测m并纠正n个错误:m+n+1（从一端考虑）

 

 

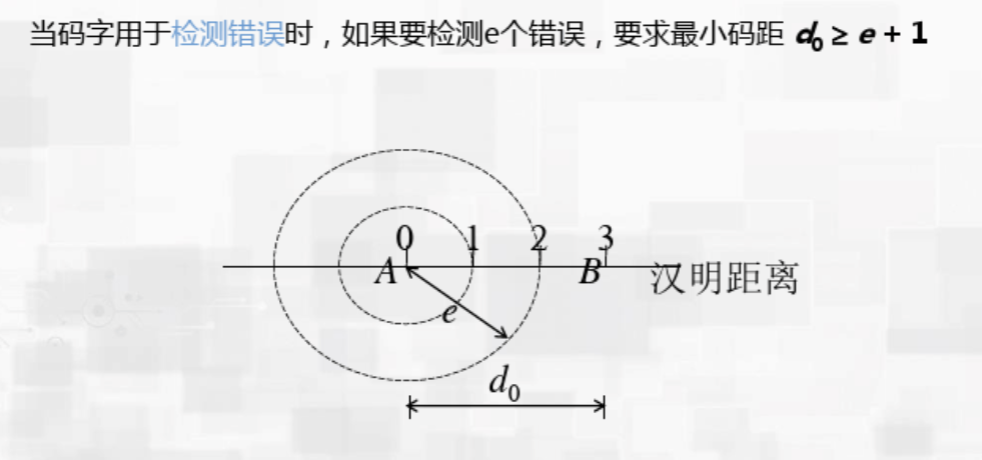
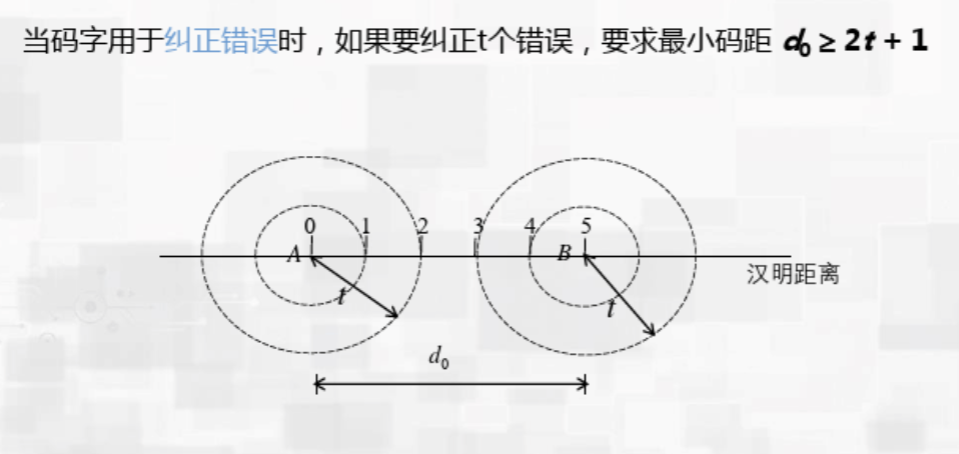
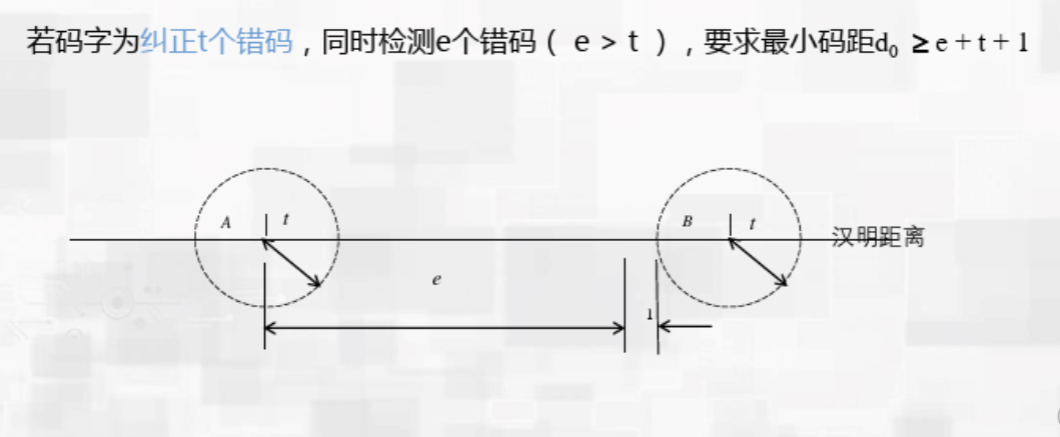
 纠错的过程与检错同理，但在发现错误时要向合法的码字靠拢来修复错误，因此需要确定哪一个码字离发生错误的码字的海明距离更近，因此就需要确定一个中心，产生了2倍关系，为了防止距离相等，又加上了一个1。可以看上面的图来理解。

海明码

海明码：m条消息位和r个校验位，能纠正所有的单个错误，是一种纠错码

校验位个数的确定: 

其中m+r为可能发生的一位错误的总数（每一位发生了错误），1为正确即合法的码字，右边2的r次方为纠错码所能覆盖的情况总数

使用海明码来纠错

计算海明码（概述，详情参考相关书籍资料）

1. 根据原有的码字来确认校验位的个数，利用上面的公式计算出r的取值
2. 校验位分布在2的幂次方位上(1,2,4,8,16,...)，其它位为原始数据位，依次填上即可
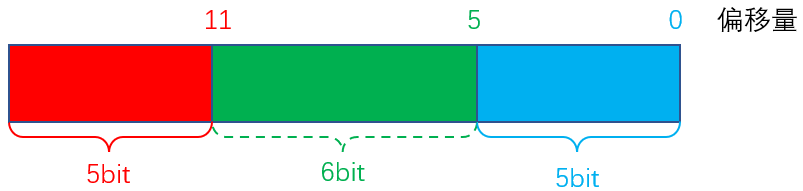
3. 计算校验位：每个校验位负责该海明码（已经确定了形式，计算除了校验位的个数，给原始数据位和校验位都按顺序编好号了）的每位的位序号用二进制拆分后包含组成该校验位的位数的2的幂数的位，对所有这些负责的位上的值进行异或运算（实质上这就是偶校验，如果1的个数为奇数异或结果为1，为偶数结果为0）

根据海明码纠错

1. 与海明码的计算过程相同，对接受到的“海明码”码字重新计算校验位，因为在发送时计算采用了偶校验，因此计算结果因为0，若为1则说明发生了错误
2. 将所有产生了错误的校验位的序号相加就得到了错误位

从上述过程可以看到，该方法只能纠正一个位的错误。从直观上理解就是采用的是偶校验，所以只能检测出单个错误，偶数个错误将无法检测到。因此将发生错误的校验位序号相加得到的就是错误的位。