秦九韶算法

什么是秦九韶算法？

        可以把多项式改写为便于递推的形式：

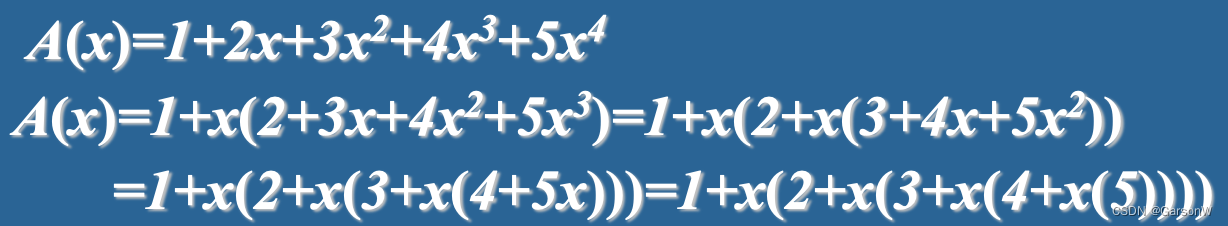
泰勒展开式

什么是泰勒展开式？

        泰勒公式，也称泰勒展开式。是用一个函数在某点的信息，描述其附近取值的公式。如果函数足够平滑，在已知函数在某一点的各阶导数值的情况下，泰勒公式可以利用这些导数值来做系数，构建一个多项式近似函数，求得在这一点的邻域中的值

        多项式   是最简单的一类初等函数。关于多项式，由于它本身的运算仅是有限项加减法和乘法，所以在数值计算方面，多项式是人们乐于使用的工具。因此我们经常用多项式来近似表达函数。这也是为什么泰勒公式选择多项式函数去近似表达给定的函数。

如何求sinx的泰勒展开式？      

        将sinx写成泰勒展开式的形式，然后等号两边分别约分。

        我们会发现等号左边是有规律的0、+1、0、-1的循环着。 

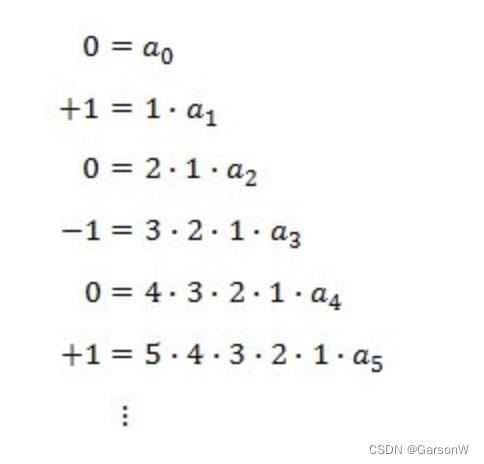
         因此，我们可以将这个规律写成以下的形式。

        这样，我们就可以推导出来每一个ak（系数）的值了。如果将系数数列 a 代入，那么偶数项都会消掉(系数为 0)，只剩下一加一减的奇数项了。

        所以，我们即可得到sinx的泰勒展开式：

 如何求sinx的近似值？

         我们可以使用SINTNV(x,n)表示利用sin(x)/x的泰勒展式取前n+1项之和作为sin(x)/x的近似值。

         当 n = 4 时，SINTNV(x,n)可以根据秦九韶算法写成以下形式：

         而后，根据秦九韶的算法可得每一项的系数：

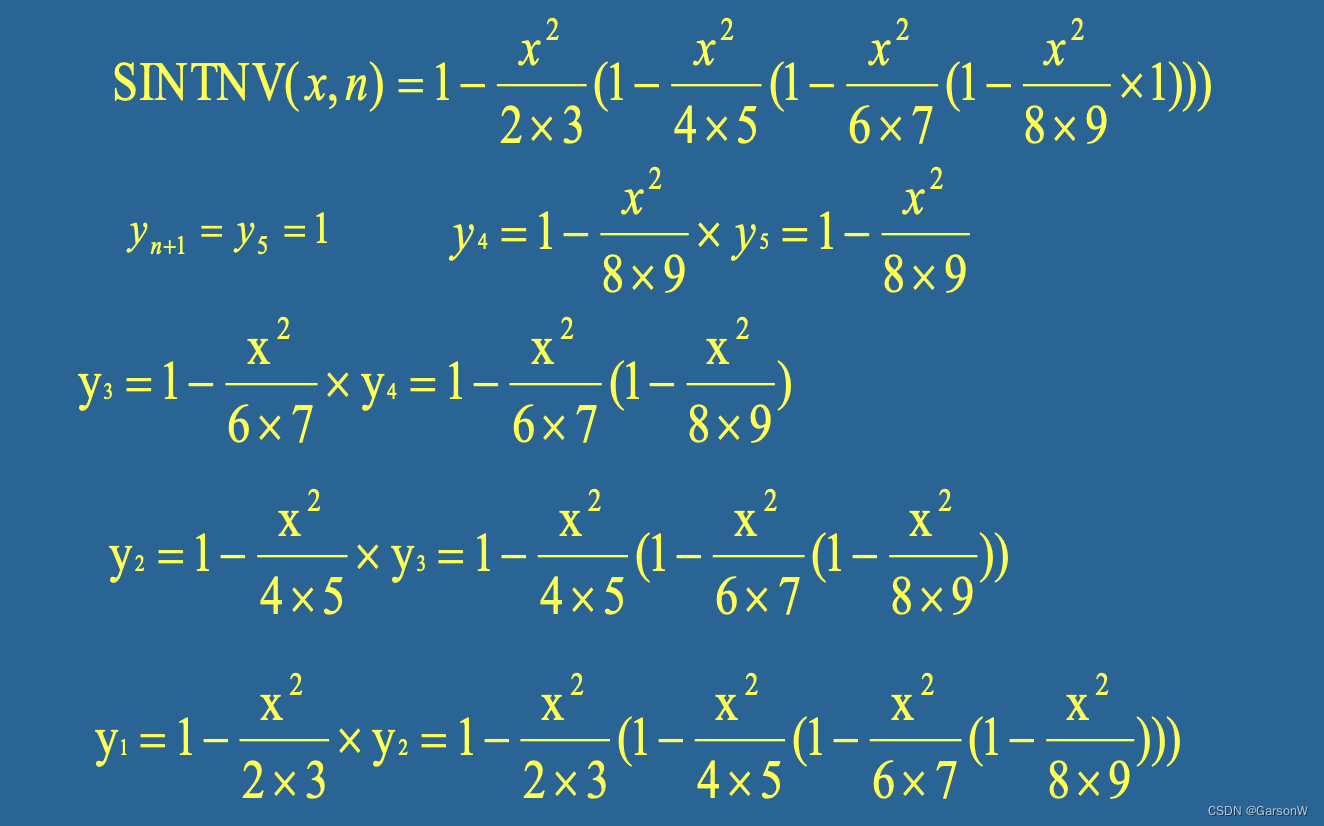
         计算出y1 ～ yn+1 从而求出sinx对应的泰勒展开式的每一项。

 如何求cosx的近似值？

        其实就是sinx的展开式分母由单数变成复数：