好久没有更新博文了,我上一篇博文的发布时间还是:![]()
题目
这是我们周考的第二道题,乍一看,很简单,仔细做,更简单。(我都没做起)



分析
我相信,很多人第一次看到这个题目就会想到暴力(我一开始就是这样的)。
但你们只要细看了过后,就能细细的品出其中的味道(递推!)
好了,暴力的方法我就不告诉你们了,我就先讲一下如何递推
首先,你得画一个图出来,我们就按照上面那个样例的图讲。你可以把他们想象在一个正方形网格中,这个正方形的便成为n.其中你只要算出在所有n的区间中,哪一个区间存在的重合的条数最多。上图

就是这样,从一算下去,会发现如果n%2==0中间两列为最大值,如果n%2==1最中间的一列为最大值。然后我们把最大的那一列抽出来看,你们可以发现这样的一个规律

在这六条线段中,长度为1,2,3,4的分别有1,2,2,1个。
然后,我们将n为1-8的所有情况列出来,可以发现下表
| 1 | 1 |
| 2 | 1,1 |
| 3 | 1,2,1 |
| 4 | 1,2,2,1 |
| 5 | 1,2,3,2,1 |
| 6 | 1,2,3,3,2,1 |
| 7 | 1,2,3,4,3,2,1 |
| 8 | 1,2,3,4,4,3,2,1 |
题目要我们所求的,只不过就是把第n行的2n-1个数全部加起来,是吧。
然后我们就可以退出以下结果:
1.如果n为奇数,则ans=((n+1)/2)*((n+1)/2)
2.如果n为偶数,则ans=(1+n/2)*(n/2)
则有如下代码:
#include<iostream>
using namespace std;
int n,maxn,sum1,sum2;
int main(){
cin>>n;
if(n%2==0){
cout<<(1+n/2)*(n/2)<<endl;
}else{
cout<<((n+1)/2)*((n+1)/2)<<endl;
}
return 0;
}
简化代码
咦?已经是O(1)的时间复杂度了,为什么还要再简化?
接下来,我来让你们大开眼界:只用一个输入一个输出就可以完成
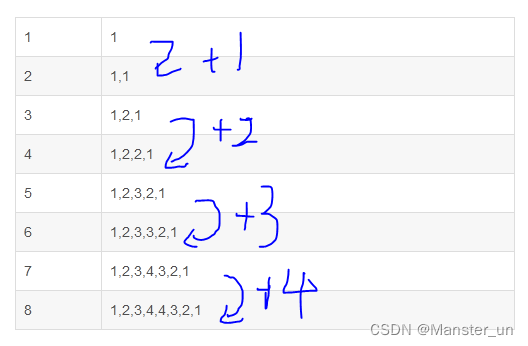
大家看了图应该都看懂了吧,如果它是奇数,我们就按照平常算,如果是偶数,那么在加一个n/2.那么额如何判断n是奇数还是偶数呢,我们只需要为n/2乘一个(n+1)%2就行了。这样的话,如果是奇数,我们就相当于加了0.完美的解决了这次的问题。
话不多说,上代码:
#include<bits/stdc++.h>
using namespace std;
int n;
int main(){
cin>>n;
cout<<((n+1)/2)*((n+1)/2)+((n+1)%2)*(n/2);
return 0;
}