目录

1、百分位数

2、数据分布

3、正态数据分布

---

1、百分位数

统计学中使用百分位数（Percentiles）提供一个数字，该数字描述了给定百分比值小于的值。

例如：假设我们有一个数组，包含一时刻一条街上人的年龄

arr = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

什么是 90 百分位数？答案是 61，这意味着 90％ 的人是 61 岁或以下。

NumPy 模块有一种用于找到指定百分位数的方法

使用 NumPy percentile() 方法查找百分位数

import numpy

ages = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

x = numpy.percentile(ages, 75)

print(x)    # 61

2、数据分布

在现实世界中，数据集要大得多，但是至少在项目的早期阶段，很难收集现实世界的数据

为了创建用于测试的大数据集，我们使用 Python 模块 NumPy，该模块附带了许多创建任意大小的随机数据集的方法

创建一个包含 250 个介于 0 到 5 之间的随机浮点数的数组

import numpy

x = numpy.random.uniform(0.0, 5.0, 250)

print(x)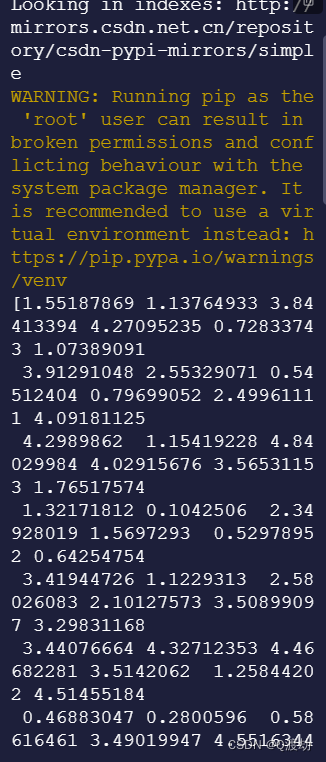

 创建一个具有 100000 个随机数的数组，并使用具有 100 栏的直方图显示它们

其中uniform() 是一个用于生成指定区间内随机浮点数的函数

import numpy as np
import matplotlib.pyplot as plt 

x = np.random.uniform(0.0, 5.0, 100000) 
plt.hist(x, 100)    # 将 0 ~ 5之间的数划分为 100 个小区间
plt.show()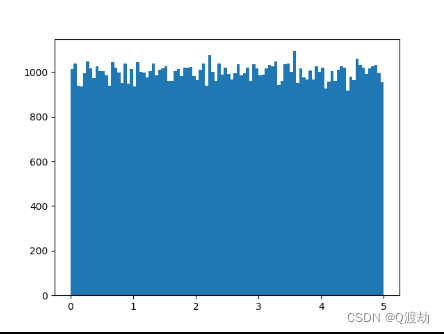

3、正态数据分布

normal`是指numpy.random 模块中的正态分布随机数生成函数

我们指定平均值为 5.0，标准差为 1.0

这意味着这些值应集中在 5.0 左右，并且很少与平均值偏离 1.0

import numpy
import matplotlib.pyplot as plt

x = numpy.random.normal(5.0, 1.0, 100000)

plt.hist(x, 100)
plt.show()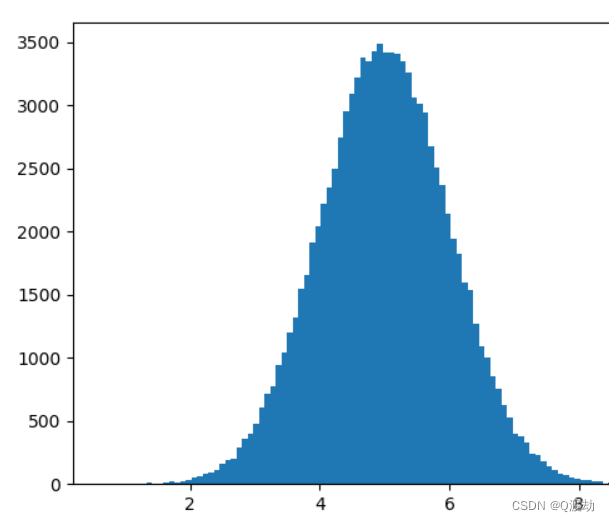

使用 numpy.random.normal() 方法创建的数组（具有 100000 个值）绘制具有 100 栏的直方图

从直方图中可以看到，大多数值都在 4.0 到 6.0 之间，最高值大约是 5.0