一、线性代数

1. 理解范数概念
2. 区分向量的内积 $\mathbf{a}\cdot \mathbf{b}$ 与外积 $\mathbf{a}\times \mathbf{b}$
3. 区分矩阵的乘法 $\mathbf{A}\otimes \mathbf{B}$、内积 $\mathbf{AB}$ 、哈达玛积 $\mathbf{A}\odot \mathbf{B}$

向量

向量是一组标量排列而成的，只有一个轴，沿着行或者列的方向。通常表示成：
$$s=\left[\begin{array}{cccc}{s}_1& s_2& \cdots & s_n\end{array}\right]或s=\left[\begin{array}{c}{s}_1\\ s_2\\ ⋮\\ s_n\end{array}\right]$$向量的模与范数

向量的长度：表示向量的维度，即向量有几个元素，比如 n 维向量 $a=(a_1,a_2,\cdots ,a_n)$ 的长度为 n，有 n 个元素。

向量的模长：简称为向量的模（Norm），表示向量在空间中的长度（欧式距离）。假设有 n 维向量 $a=(a_1,a_2,\cdots ,a_n)$，其模长 $\Vert a\Vert$ 等于 $\sqrt{a_1^2+a_2^2+\cdots +a_n^2}$。

向量的范数：$\Vert x\Vert =({\sum }_i|x_i{|}^p{)}^{\frac{1}{p}}$，其中 $p\in R,p\ge 1$。通常存在 $L_2$ 范数或者 $L_1$ 范数，其中 $1$ 和 $2$ 对应公式中的 $p$ 值。向量的模长就为 $L_2$ 范数。

单位向量

单位向量：即模长为 1 的向量，通常用于表示向量在空间中的方向，而不是长度（长度为模）。

假设有 n 维向量 $a=(a_1,a_2,\cdots ,a_n)$，其单位向量为$$\frac{1}{\sqrt{a_1^2+a_2^2+\cdots +a_n^2}}(a_1,a_2,\cdots ,a_n)$$向量的内积

向量的内积（Inner Product）：也成为点乘、点积，是向量对应位置元素相加再相乘，结果为一个标量。

假设有向量 $\mathbf{a}=(a_1,a_2,\cdots ,a_n)$，$\mathbf{b}=(b_1,b_2,\cdots ,b_n)$，那么其内积 $\mathbf{c}$ 为：$$\begin{array}{rl}\mathbf{c}& =\mathbf{a}\cdot \mathbf{b}\\ & =\sum _{i=1}^n{a}_i\cdot b_i\end{array}$$向量内积的几何意义：能够表示出两个向量之间的线性相关程度，假设两个向量 $\mathbf{a}=(a_1,a_2,\cdots ,a_n)$，$\mathbf{b}=(b_1,b_2,\cdots ,b_n)$，那么其夹角 $\theta$ 余弦值 $\cos \theta$ 就为：$$\cos \theta =\frac{\mathbf{a}\cdot \mathbf{b}}{\Vert a\Vert \Vert b\Vert }$$当 $\cos \theta =0$，表示两个向量空间垂直，即向量无关；当 $\cos \theta =1$，表示两个向量空间方向相同，即线性高度相关。

向量的外积

外积（Outer Product）：也称为向量叉积、叉乘，其计算结果是一个向量，其方向垂直于两个向量组成的平面。

假设有两个向量 $\mathbf{a}=(a_1,a_2,\cdots ,a_n)$，$\mathbf{b}=(b_1,b_2,\cdots ,b_n)$，那么向量外积 $\mathbf{c}$ 表示为 $\mathbf{c}=\mathbf{a}\times \mathbf{b}$，其大小为：$$\left|c\right|=\left|a\right|\left|b\right|\sin (\mathbf{a},\mathbf{b})$$

矩阵

矩阵是由多个元素组成的表格，是一种二维结构，每个数字在矩阵中对应一个行号与列号。矩阵表示如下：$$A=\left[\begin{array}{cccc}{A}_{1,1}& A_{1,2}& \cdots & A_{1,n}\\ A_{2,1}& A_{2,2}& \cdots & A_{2,n}\\ ⋮& ⋮& & ⋮\\ A_{m,1}& A_{m,2}& \cdots & A_{m,n}\end{array}\right]$$矩阵的转置

矩阵的转置（Transpose）是将矩阵以主对角线为轴，进行镜像翻转，$(A{)}_{m,n}^T=A_{n,m}$。

矩阵乘法

假设有矩阵 $A_{m,k}$ 和矩阵 $B_{k,n}$，那么矩阵乘法表示为：$$C=A\otimes B=AB\Rightarrow C_{m,n}=\sum _k{A}_{m,k}{B}_{k,n}$$

矩阵乘法能操作的前提是：矩阵 $A$ 的列数必须与矩阵 $B$ 的行数相同！

矩阵内积

矩阵内积表示将两个矩阵对应元素直接相乘再相加，结果为一个标量。$$c=\sum _{i=1}^m\sum _{j=1}^n{A}_{i,j}{B}_{i,j}$$

矩阵哈达玛积

矩阵的哈达玛积（Hadamard product）表示将两个矩阵对应元素相乘，其结果是一个矩阵。$$\mathbf{C}=\mathbf{A}\odot \mathbf{B}\Rightarrow \mathbf{C}=\left[\begin{array}{cccc}{A}_{1,1}{B}_{1,1}& A_{1,2}{B}_{1,2}& \cdots & A_{1,n}{B}_{1,n}\\ A_{2,1}{B}_{2,1}& A_{2,2}{B}_{2,2}& \cdots & A_{2,n}{B}_{2,n}\\ ⋮& ⋮& & ⋮\\ A_{4,1}{B}_{4,1}& A_{4,2}{B}_{4,2}& \cdots & A_{4,n}{B}_{4,n}\end{array}\right]$$张量

张量（Tensor）是多维数组的抽象概括，可以看作是向量和矩阵的扩展，这也是 Pytorch 中最基本的数据结构。

二、微积分

梯度

梯度是一个包含所有偏导数的向量，用符号 $\nabla$ 表示。

比如有函数 $z=f(x,y)=x^2+y^2$，其梯度向量为：$\nabla f(x,y)=(2x,2y)$。

在梯度下降算法中，参数的更新公式为：${\theta }_{t+1}={\theta }_t-\eta {\nabla }_{\theta }J({\theta }_t)$。

方向导数与梯度的关系，方向导数表示某一个点处沿各个方向的斜率，是一个标量。而梯度是一个向量，其方向上的方向导数最大，其大小正好是此最大方向导数。

三、概率

贝叶斯定理

贝叶斯定理公式：$$P(A|B)=P(A)\frac{P(B|A)}{P(B)}$$

英国数学家托马斯·贝叶斯（Thomas Bayes）在 1763 年发表的一篇论文中，首先提出了该定理。

该论文表示贝叶斯为了解决一个 ”逆概率” 问题，而提出了贝叶斯定理。在贝叶斯写这篇论文前，人们已经能够计算 “正向概率” 问题了。

正向概率问题就比如从箱子中摸球的问题，假设箱子中有 2 个白球、2 个黑球，你从箱子中摸一次且只拿一个球，那么抽到白球的概率是多少？这种从 已知信息 到 未知信息 的问题就是正概率问题。

逆概率问题就比如上面摸球问题，在之前并不知道箱子里面有什么颜色的球，而是摸出一个球，观察这个球的颜色，进而预测这个箱子里面有什么颜色的球，这种从 未知信息 到已知信息 的问题就是逆概率问题。

在平时生活中，大部分问题都是 “逆概率” 问题。因为绝大多数决策面临的信息都是不完整的，我们手中只有有限的信息。既然无法得到完整的信息，就只能在有限信息的条件下，尽可能做出一个好的预测。

而对于贝叶斯公式可以这么理解，比如一个例子：我喜欢吃冰淇淋，然后偶然在抖音上刷到有人推荐肯德基的冰淇淋很好吃，那么现在我想知道肯德基的冰淇淋到底好不好吃。

那么现在有：

• 要求解的问题（未知信息）：肯德基的冰淇淋是否好吃，记为事件 A；
• 已知条件：抖音上有人推荐肯德基的冰淇淋好吃，记为事件 B；

所以 $P(A|B)$ 就表示在抖音上有人推荐肯德基的冰淇淋好吃的事件发生后，肯德基的冰淇淋好吃的概率。那么有贝叶斯公式：$$P(A|B)=P(A)\frac{P(B|A)}{P(B)}$$对公式可以这样看：

• $P(A|B)$：后验概率
• $P(A)$：先验概率（Prior Probability），表示在不知道事件 B 的前提之下，我们认为对事件 A 的一个主观判断。
• $\frac{P(B|A)}{P(B)}$：可能性函数（Likelyhood），它是一个调整因子，即为新信息 B 带来的调整，其作用是将先验概率（之前做的主观判断）调整到更接近真是的概率。
  • 当 $\frac{P(B|A)}{P(B)}>1$ 表示先验概率被增强，事件 A 发生的概率变大；
  • 当 $\frac{P(B|A)}{P(B)}<1$ 表示先验概率被削弱，事件 A 发生的概率变小；
  • 当 $\frac{P(B|A)}{P(B)}=1$ 表示事件 B 无助于判断事件 A 的可能性。

极大似然估计

概率：在特定环境下某件事情发生的可能性，即在结果没有产生之前，根据环境中的参数，来预测某件事情发生的概率。比如抛硬币，在没有抛之前，我们并不知道结果会是硬币的那一面朝上。但是根据硬币的性质，可以推测得出任何一面朝上的概率都是 0.5。而这里的概率 0.5，只有在抛硬币之前是有意义的。因为硬币抛完了之后，结果就确定了。

似然：基于已经确定的结果，来推测产生这个结果的可能环境，或者说是推测环境中的某些参数。比如抛硬币，假设随机抛出硬币 10000 次，结果 8000 次人像在上，2000 次数字在上，就可以推测出该硬币可能比较特殊，进而可得该硬币的具体参数，即人像的概率为 0.8，数字的概率为 0.2。这种根据结果判断事情本身性质的过程就是似然。

假设 $\theta$ 表示环境对应的参数，而 $x$ 表示事件发生的结果，就有

• 概率表示为 $P(x|\theta )$，在环境参数为 $\theta$ 的前提下，事件 $x$ 发生的概率，其中 $P$ 是关于 $x$ 的函数。
• 似然表示为 $L(\theta |x)$，在已知观察结果为 $x$ 的前提下，来推断 $\theta$，其中 $L$ 是关于 $\theta$ 的函数。

极大似然估计（Maximum Likelihood Estimate）：也称为最大似然估计，利用已知的样本标记结果，反推最具有可能，或者说是最大概率导致这些样本结果出现的模型参数。极大似然估计是一种已知观察数据来推断模型参数的过程。

利用抛硬币的例子，假设 $P(人像朝上)=\theta$，$P(数字朝上)=1-\theta$，$\theta$ 存在但是具体未知。

为了获取 $\theta$，进行抛硬币实验并记录抛出的结果序列。假设在这个序列中，有 7 次是人像朝上，3 次是数字朝上，那么就有 $\theta$ 的似然函数$$L(\theta )={\theta }^7(1-\theta {)}^3$$其函数图像如下：

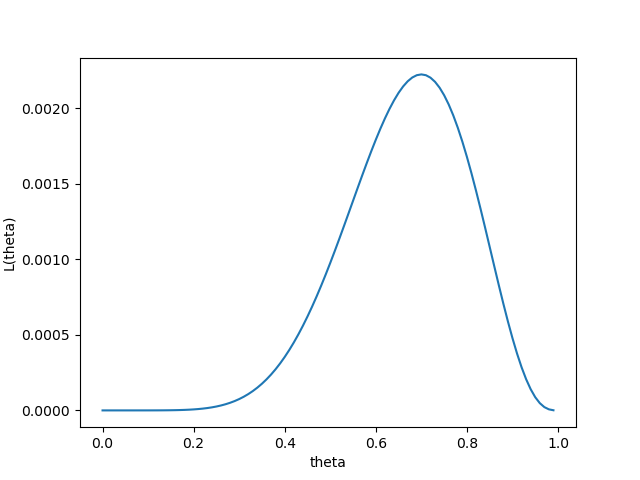
最大似然估计就是求解当 $\theta$ 取值为多少的时候，似然函数 $L(\theta )$ 取得最大值，即 10 次实验最可能发生 7 次是人像朝上，3 次是数字朝上。

为了获取更准确的参数，可以增加试验次数。