最近两个多月在实习，做的是GPS定位相关的一些工作，同时也简单做了一下组合导航。卡尔曼滤波是组合不同传感器比较核心的算法，应用也比较广泛，也有很多文章对其进行了详细的介绍，这里记录一下自己的一些理解。

优秀的博客推荐

这里必须要分享一篇博客，在我了解卡尔曼滤波的开始，看过很多上来就给你列出一堆公式或者说一堆让你看不懂的教材或者文章，让人从入门到放弃。但是这篇博客写的非常浅显易懂，可以说让我耳目一新，不得不佩服作者的写作风格，原文链接：How a Kalman filter works, in pictures

里面的语言也很通俗，遇到看不懂的用翻译软件翻译一下也完全够了。

直观理解

简单以上面博客的内容举个例子。假设小机器人在一维方向需要估计自己走了多远。现在有两类数据：

• 在起点有一个仪器，可以测量现在的位置距离起点有多远
• 同时可以小机器人可以给出自己的速度信息

由此，首先小机器人已知

• 传感器测量的离起点的距离（称之为观测值,比如雷达直接测量机器人离障碍物距离7m)
• 上个时刻机器人离起点距离
• 自己当前时刻的速度

而根据 上个时刻机器人离起点距离 和 自己当前时刻的速度 可以估算出当前机器人离起点的距离（称之为估计值）。例如：上一秒离起点2m，速度是4m/s，那么现在这秒估计就离起点距离是6m。但是这个时刻传感器测量的离起点的距离是7m。

那么问题来了，机器人离起点的距离现在既有个观测值7m，又有个估计值6m。到底相信哪个？单纯相信观测值万一那传感器坏了呢？单纯相信估计值那么万一上个时刻的距离估计值或者速度不准呢？所以，我们要根据观测值和估计值的准确度来得到最终机器人离起点的距离估计值。准确度高的就最终结果比重高，准确度低就占比低。

如果雷达测量的那个7m准确度是90%，根据速度估计出的那个6m准确度是80%，那么最终的距离估计结果就是 **0.8/(0.8+0.9)6+0.9/(0.8+0.9)7=6.52米。

事实上，0.9/(0.8+0.9) 就是所谓的卡尔曼增益,它就是表示这个传感器数据相对于根据速度计算出的估计值的靠谱程度。(每个传感器在使用前都可以对它的噪声的方差进行测量,比如IMU有对应的Allen方差）

卡尔曼滤波核心算法

重复的我也不多说了，根据上面的博客我们可以得到卡尔曼滤波的五个核心公式：
（以下公式截图均来自于i2Nav实验室的组合导航课程讲义）

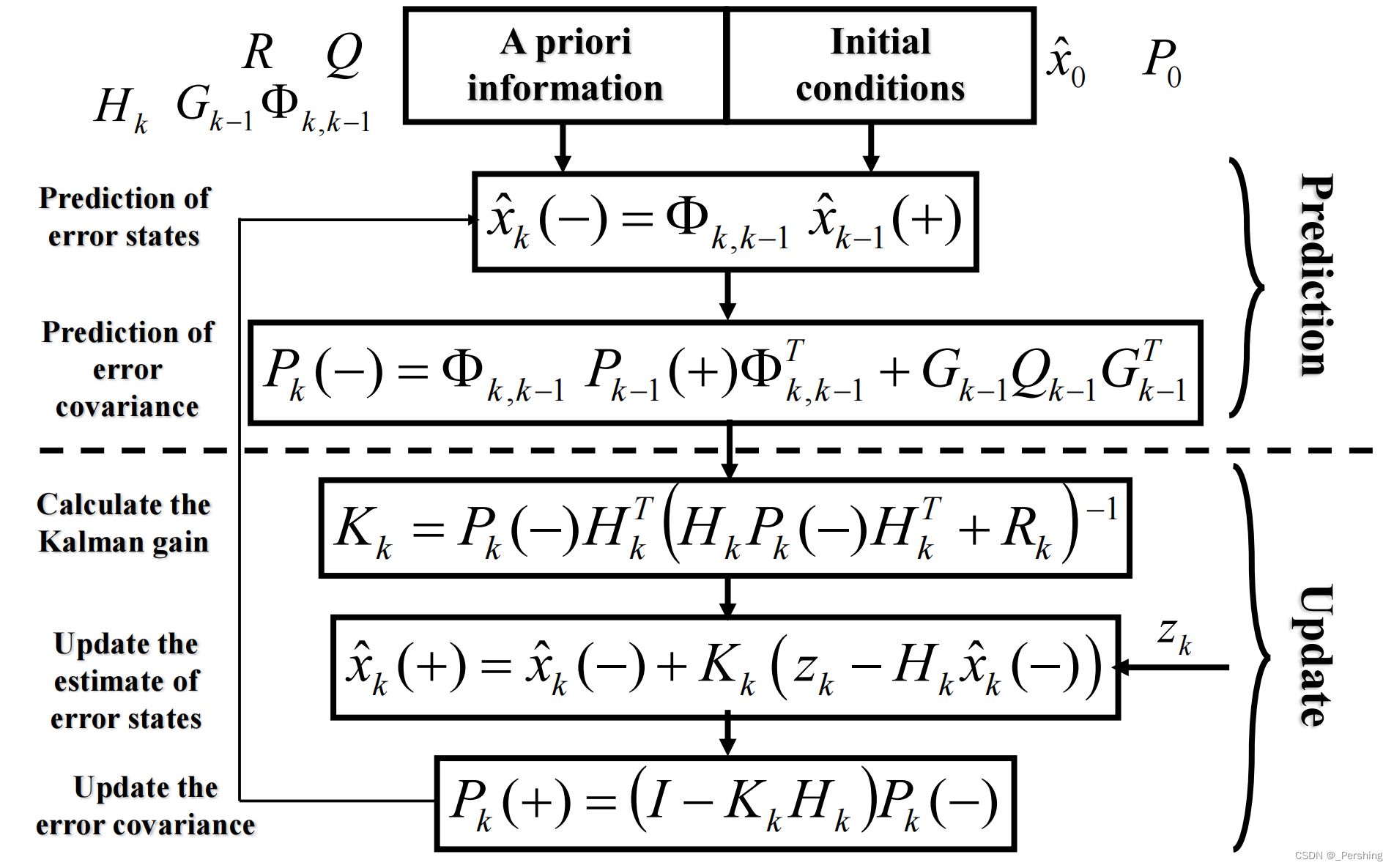
• 思路就像把上述的简单的值变成了一个矩阵，$\hat{x}$是状态向量 ，$\varphi$是状态转移矩阵，例如是运动方程的参数，因此第一个公式利用上一个时刻的状态向量${\hat{x}}_{k-1}(+)$乘上 $k-1$ 到 $k$ 状态的状态转移矩阵就可以得到这个时刻的状态向量预测值${\hat{x}}_k(-)$，为什么是预测值呢？因为是用状态转移矩阵直接乘出来了，没有加任何的观测约束。所以下一步就是要进行观测值对状态的更新修正。注意到更新之前还需要把状态向量对应的协方差矩阵也更新了，协方差在更新的时候需要主要误差的引入。这样第一步的预测过程就完成了。
• 在利用观测值更新的时候首先要计算卡尔曼增益$K_k$，卡尔曼增益即权重，决定了下一步哪个传感器的权重大哪个小，推到过程需要用正太分布的特性去计算，具体计算过程可以参考这篇博客：卡尔曼增益推导
• 卡尔曼增益计算完后对状态向量进行更新，注意到后面的括号中是$z_k-H_k{\hat{x}}_k(-)$，其中$z_k$是观测值，$H_k$是观测矩阵，${\hat{x}}_k(-)$是状态向量预测值，那观测矩阵乘以状态向量预测值应该得到什么呢？没错，就是预测的观测值，因此这一步实际是用真实的观测值减去预测的观测值，求出之间的差值再乘以卡尔曼增益。
  • 假设$K_k$很大，$K_k{H}_k{\hat{x}}_k(-)$与${\hat{x}}_k(-)$基本消去，${\hat{x}}_k(+)\approx Z_k$
  • 假设$K_k$很小，后面与等于0，${\hat{x}}_k(+)\approx {\hat{x}}_k(-)$
  • 因此可以看出卡尔曼增益就是起到该相信那部分数据的作用
• 最后再根据卡尔曼增益更新误差协方差矩阵$P_k$，显然$(I-K_k{H}_k)<I$，所以 $P_k(+)<P_k(-)$，这表明经过一次滤波，融合观测值信息会降低误差，而降低多少，就得看观测值起到的作用有多大了。
• 这样一直的循环修正，一个迭代的过程。

举个例子

卡尔曼滤波中的矩阵，以IMU+GNSS松组合为例，其中IMU是系统的运动估计，GNSS得到的位置坐标作为观测值输入。

常见系统状态含有位置、速度、姿态、传感器误差等是21x1大小的矩阵，常见GNSS测量值包含经度、纬度、高程是3x1大小的矩阵。即状态空间 $\hat{x}$是21维，观测空间 $z$ 是3维。

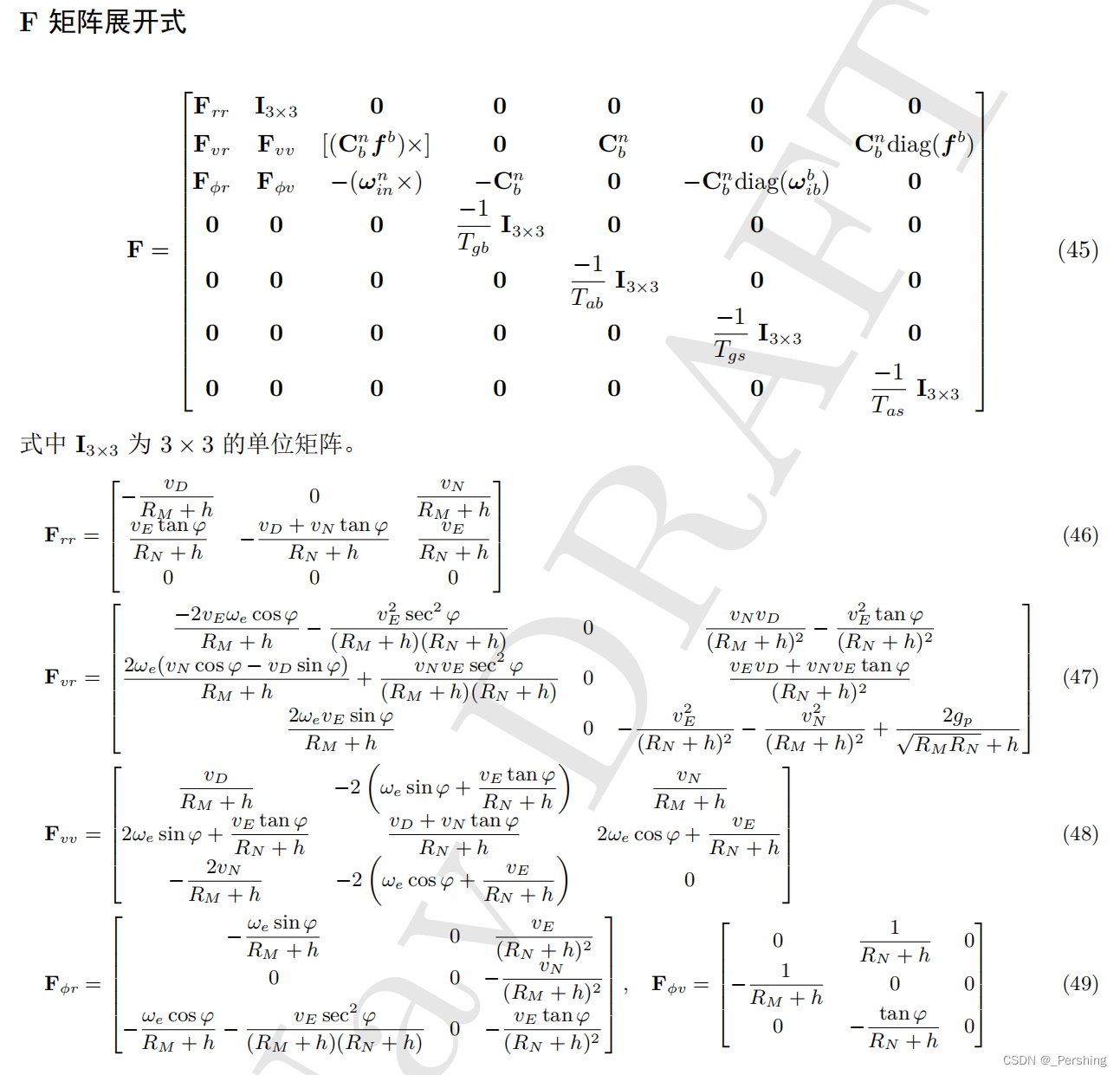
• $F$ ——状态转移矩阵：根据上一刻状态，进行系统状态预测；大方阵 21x21维
  

• $H$——观察矩阵：根据系统状态，胖矩阵，3x21维
  

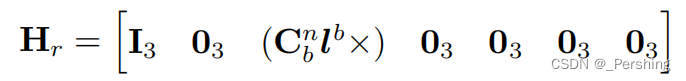
• $K$——卡尔曼增益，这是一个瘦矩阵，21x3维，直观意义是代表了对观测结果（GNSS）的接受程度，同时，还兼具把观测空间 $z$ 转换到 $\hat{x}$ 空间的功能。

• $P$——状态估计矩阵，这是一个大方阵，21x21维

• $Q$——运动噪声矩阵（IMU的噪声），这是一个中型方阵，取决与IMU的噪声模型，比如考虑零偏，随机游走，读数非线性， 3x3(三维）x2(陀螺仪/加计）=18， 则Q阵是18x18维，中方阵
  

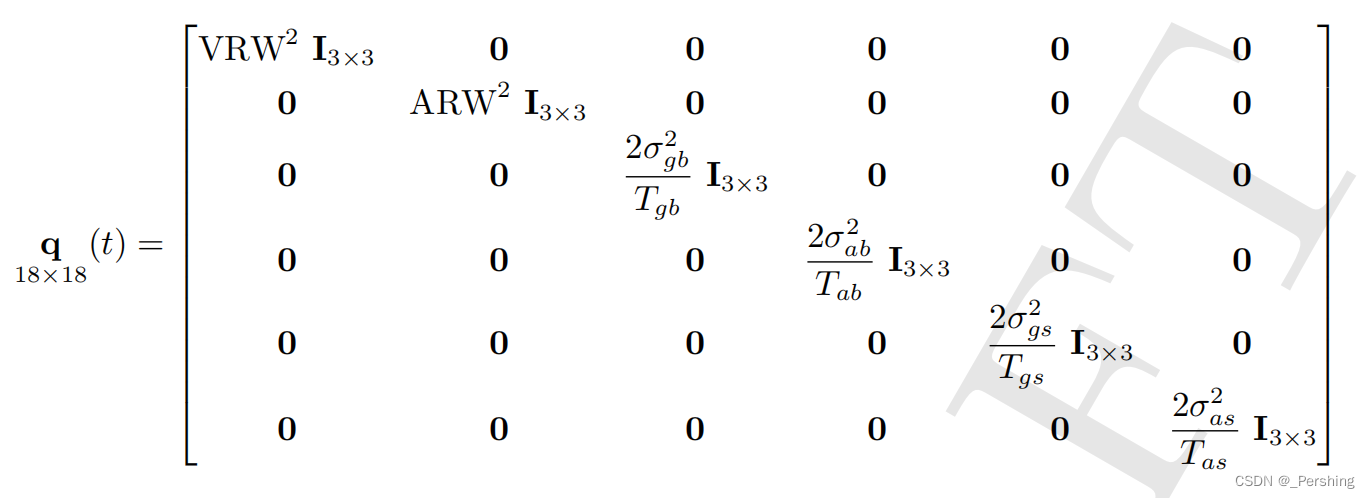
• $R$——观察噪声矩阵（GNSS的噪声），只考虑经纬高，则是3x3，小方阵

• $G$——G矩阵，