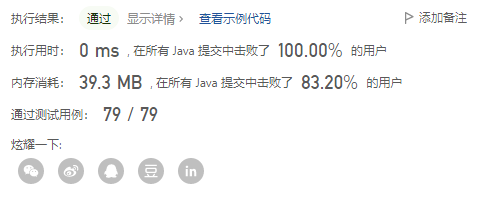
文章目录
- 1. priority_queue的介绍和使用
- 1.1 priority_queue的介绍
- 1.2 priority_queue的使用
- 1.2.1 仿函数介绍
- 1.2.2 在OJ中的使用:数组中的第K个最大元素
- 思路1:排序
- 思路2:priority_queue
- 思路3:TOP-K思想
- 2. priority_queue的模拟实现
- 2.1 核心接口
- 2.2 向上调整
- 2.3 向下调整
- 2.4 仿函数less和greater模拟实现及使用
- 3. priority_queue 存放自定义类型数据
- 4. 拓展
这篇文章我们接着上一篇的内容,再来学一个STL里的容器适配器——
priority_queue(优先级队列)
1. priority_queue的介绍和使用
1.1 priority_queue的介绍
我们上一篇文章学了queue(队列),那优先级队列也是在<queue>里面的:
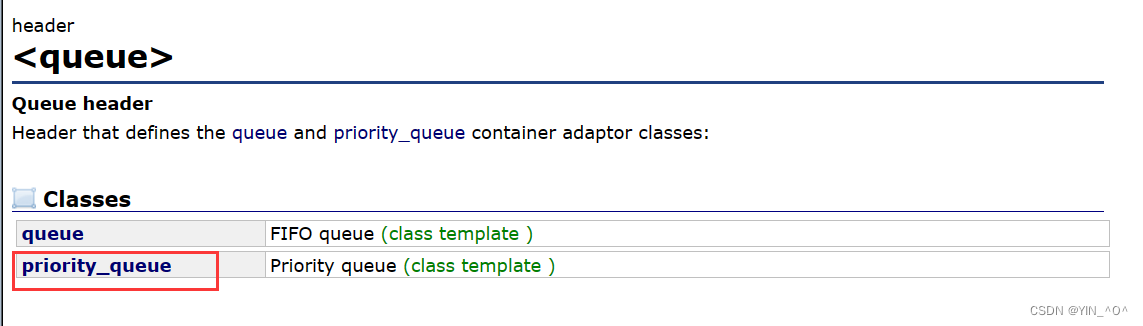
和queue一样,priority_queue也是一个容器适配器,那他和queue有什么区别呢?我们一起来认识一下priority_queue:
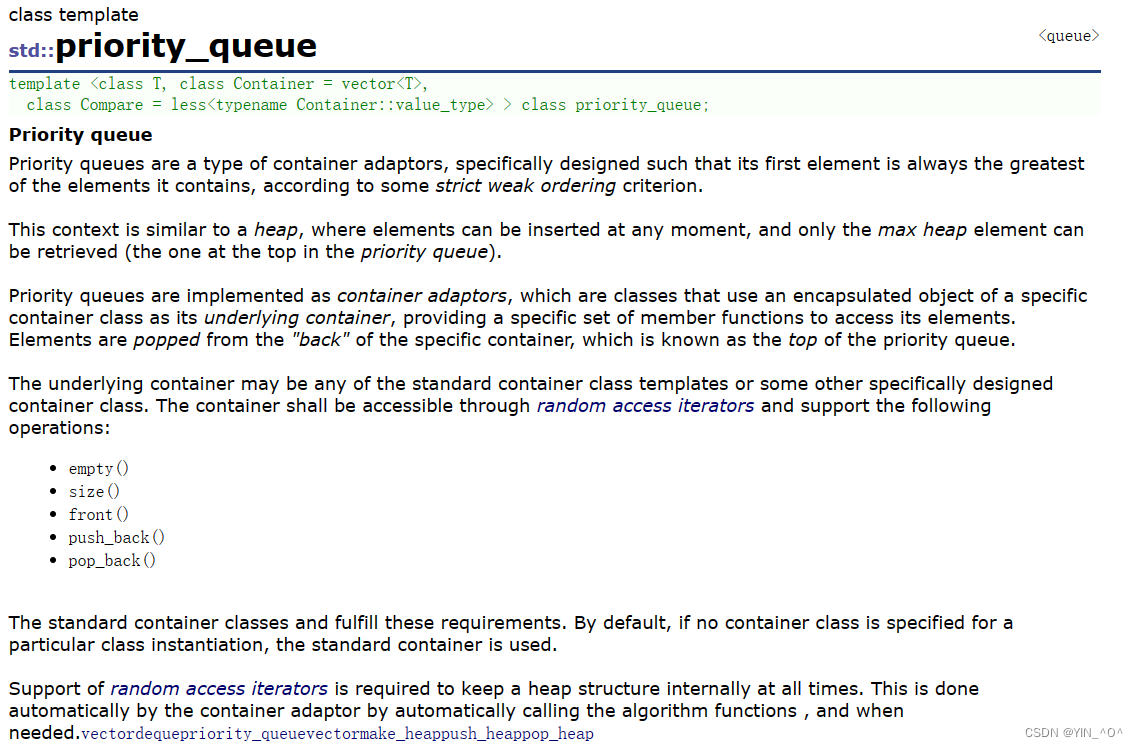
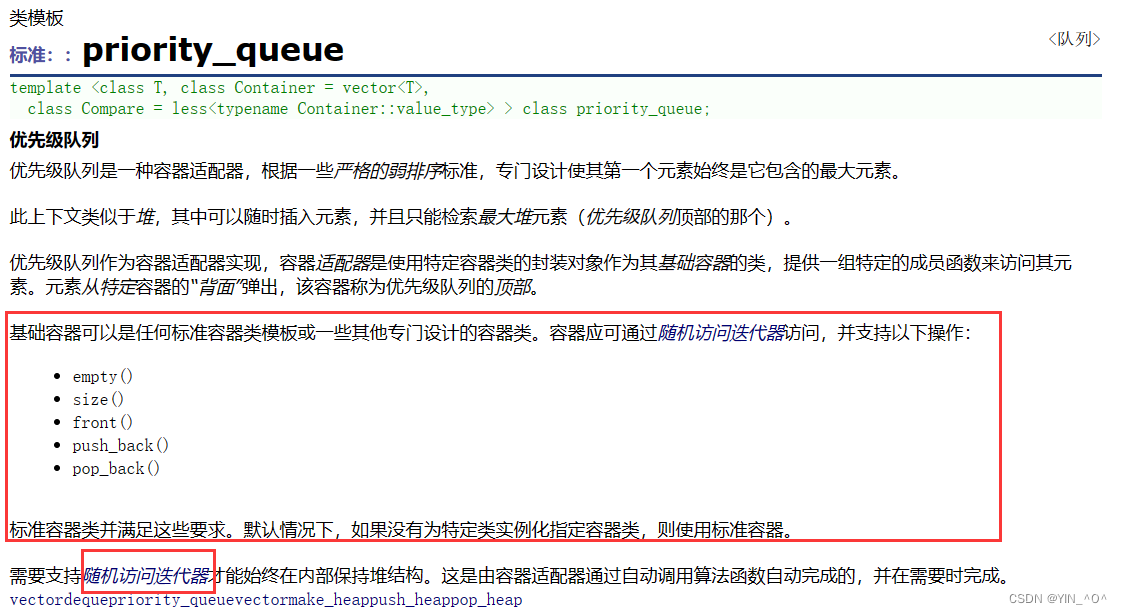
- 优先队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素总是它所包含的元素中最大的。
- 此上下文类似于堆,在堆中可以随时插入元素,并且只能检索最大堆元素(优先队列中位于顶部的元素)。
- 优先队列被实现为容器适配器,容器适配器即将特定容器类封装作为其底层容器类,queue提供一组特定的成员函数来访问其元素。元素从特定容器的“尾部”弹出,其称为优先队列的顶部。
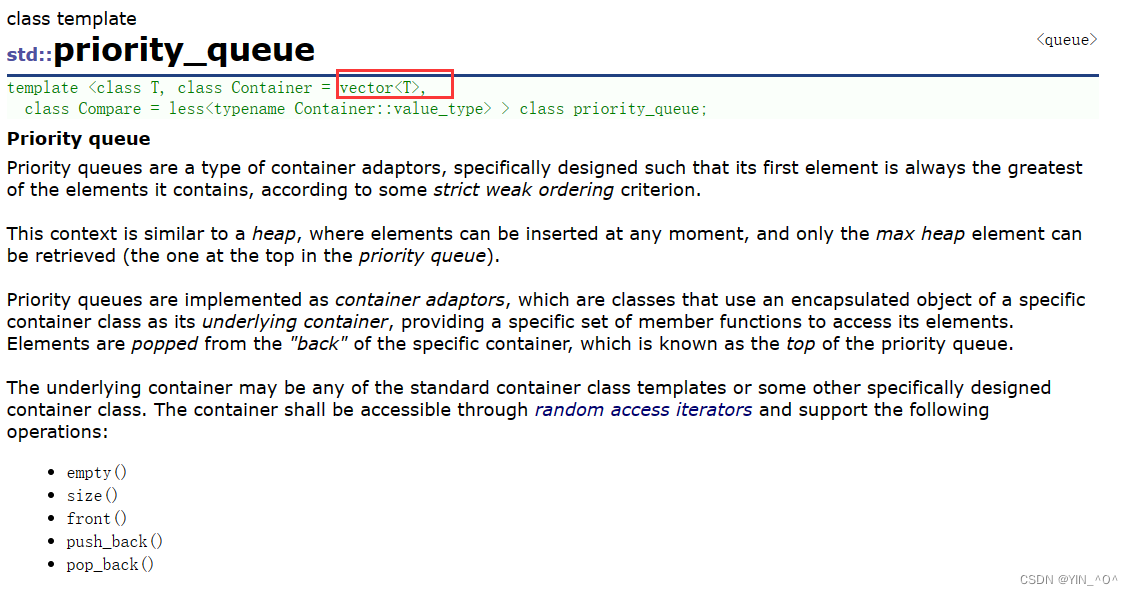
- 底层容器可以是任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问,并支持以下操作:
empty():检测容器是否为空
size():返回容器中有效元素个数
front():返回容器中第一个元素的引用
push_back():在容器尾部插入元素 - 标准容器类vector和deque满足这些需求。默认情况下,如果没有为特定的priority_queue类实例化指定容器类,则使用vector。
- 需要支持随机访问迭代器,以便始终在内部保持堆结构。容器适配器通过在需要时自动调用算法函数make_heap、push_heap和pop_heap来自动完成此操作。
首先我们看到它的默认底层容器不再是deque了,而是vector。
当然不是只能用vector,只要支持这些操作的容器都可以,另外我们看到他对容器的迭代器是有要求的,要求得是随机迭代器random access iterators。
那现在问一下大家,听到优先级队列有没有感到有点熟悉?
或者我们可以来看一下它的成员函数:
有没有感觉有点熟悉?
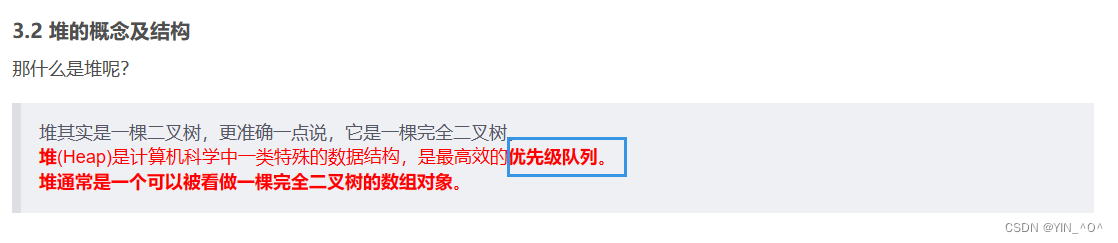
🆗,这不就是我们之前数据结构学过的堆嘛(如果大家之前没有了解过堆或者遗忘了可以去看一下之前的文章)
我们在讲解堆的时候也提到过,优先级队列就是堆。
1.2 priority_queue的使用
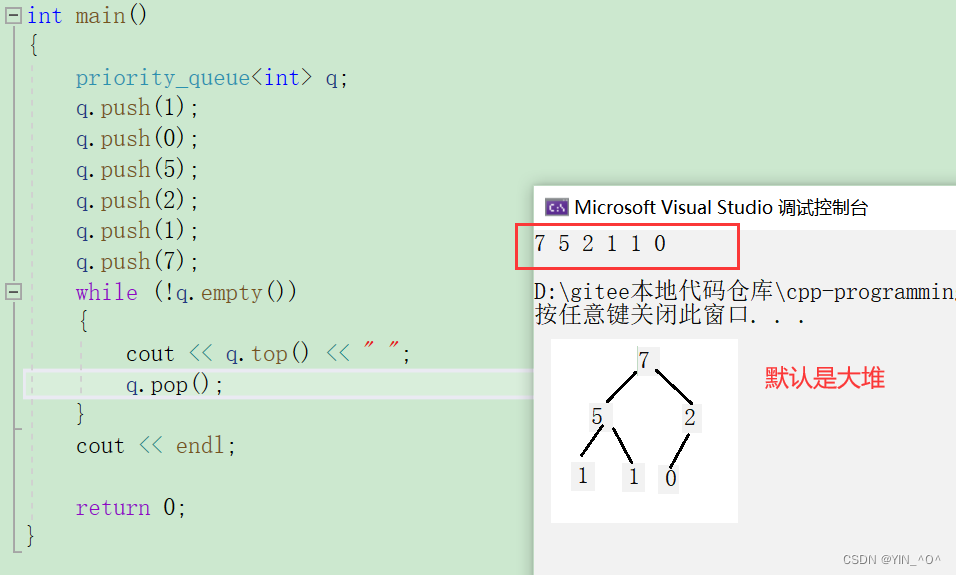
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。注意:默认情况下priority_queue是大堆。

经过数据结构阶段的学习,这些常见的接口我们是可以直接上手使用的,其它的接口如果后续用到大家可以自己查阅文档,这里就不展开介绍了。
【注意】
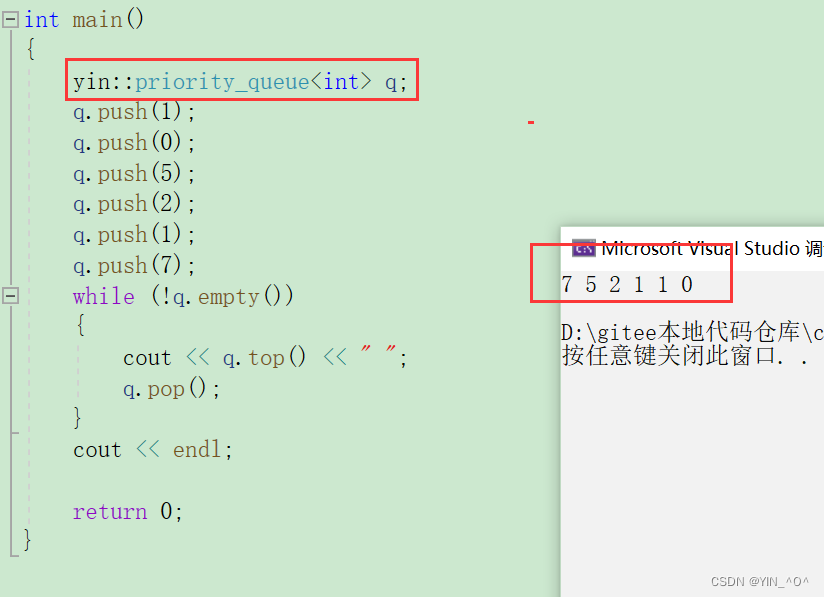
默认情况下,priority_queue是大堆(大的优先级高)
我们来验证一下:
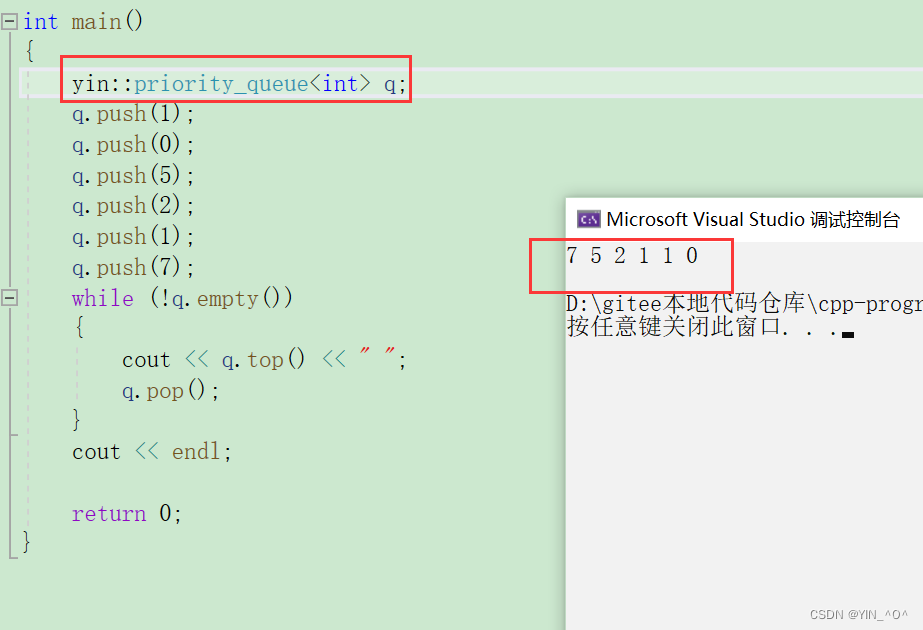
int main()
{
priority_queue<int> q;
q.push(1);
q.push(0);
q.push(5);
q.push(2);
q.push(1);
q.push(7);
while (!q.empty())
{
cout << q.top() << " ";
q.pop();
}
cout << endl;
return 0;
}
看一下结果:
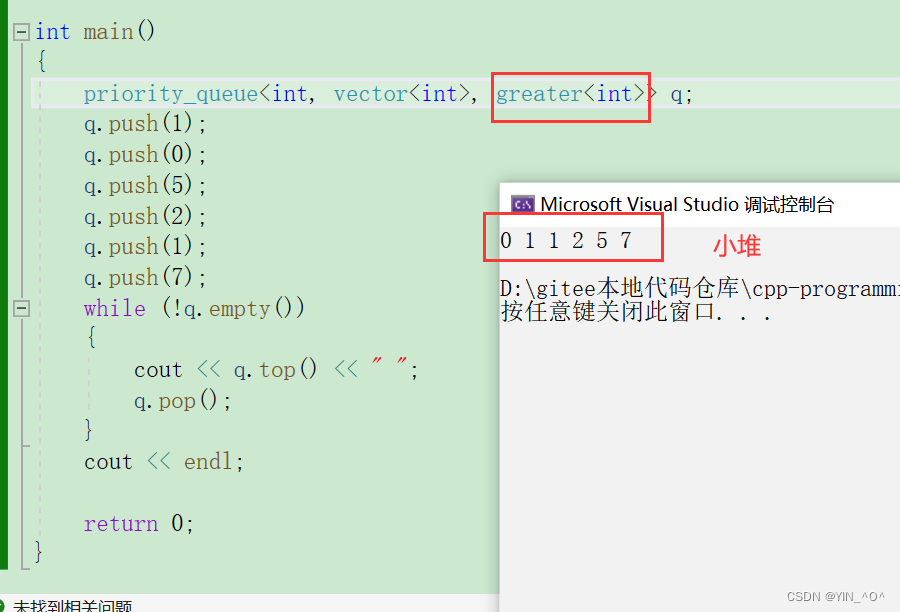
那如果我们想使用小堆怎么做呢?
🆗,这时候就要用到一个东西叫做仿函数。
怎么做呢?
我们要多传一个参数,即对应第三个模板参数。
不过呢,因为Compare这个模板参数被设计在了第三个位置,所以我们要传第三个的话,也要传一下第二个。
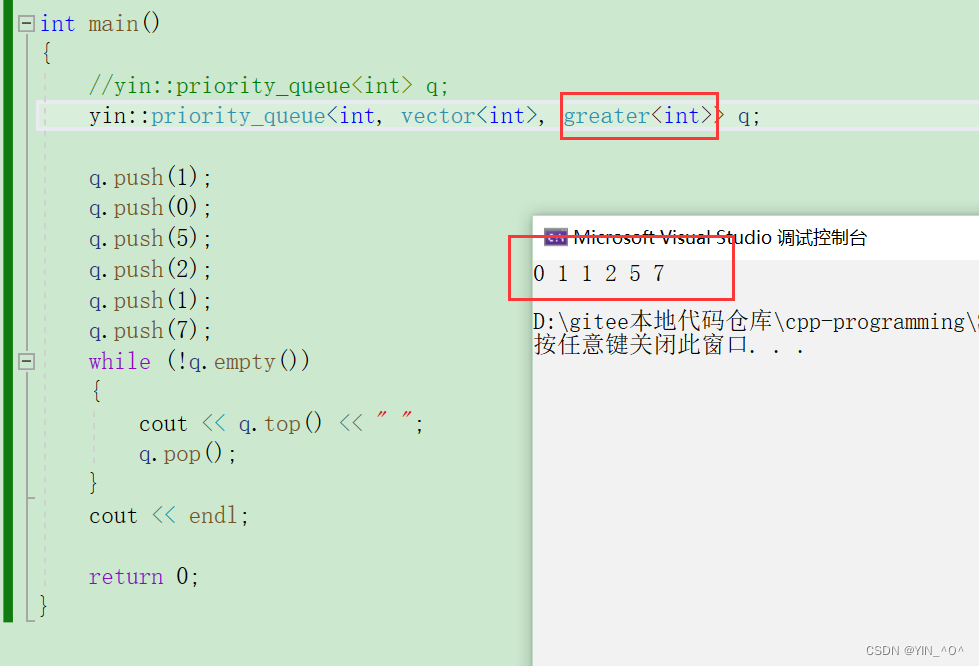
那我们现在优先级队列里面放的是整型,就可以传一个greater<int>,让它变成大堆:
int main()
{
priority_queue<int, vector<int>, greater<int>> q;
q.push(1);
q.push(0);
q.push(5);
q.push(2);
q.push(1);
q.push(7);
while (!q.empty())
{
cout << q.top() << " ";
q.pop();
}
cout << endl;
return 0;
}
那这个地方大家可能有这样的疑惑:
我们看到第三个模板参数给的缺省值是less <value_type>,less不是较小的意思嘛,但是默认对应的却是大堆;而我们把它变成小堆传的是greater <value_type>,而greater却是较大的意思。
那除此之外:
第二个模板参数是不是放到第三个位置比较好一点啊,因为默认容器我们一般不会去动它,但是第三个参数控制这个优先级,我们可能需要经常换,那这样我们传递三个参数的时候就必须把第二个也传上,但第二个一般我们不需要动,用默认的就是比较好的。
所以这个地方感觉设计的好像不是很好。
1.2.1 仿函数介绍
然后我们来解释一下这里用到的
greater<int>是个啥?
那我们先来认识一个东西——仿函数。
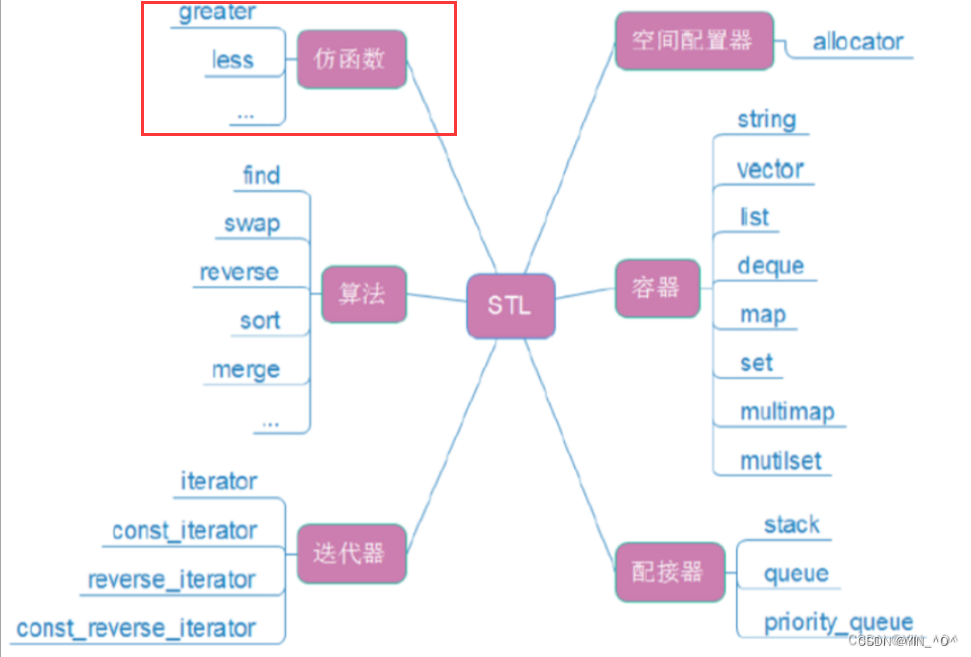
他也是STL的六大组件之一。
那什么是仿函数呢?
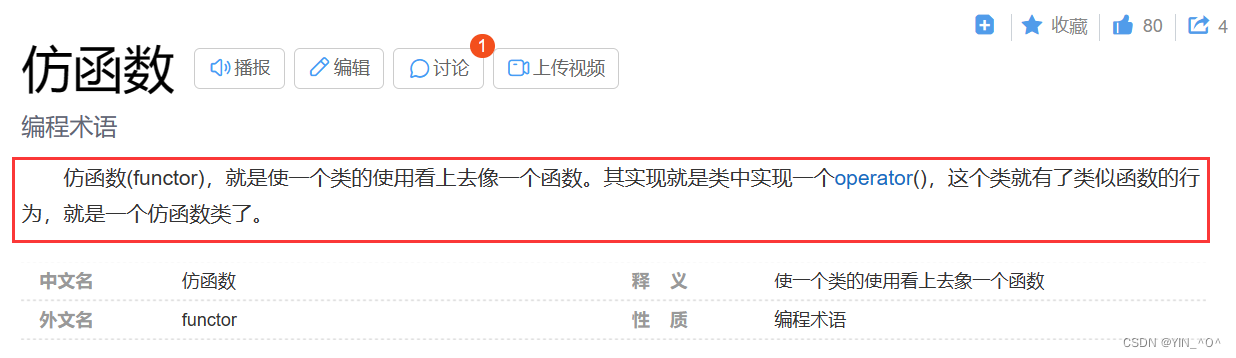
🆗,仿函数(又称函数对象)其实就是一个类重载了(),使得这个类的使用看上去像一个函数。
举个栗子:
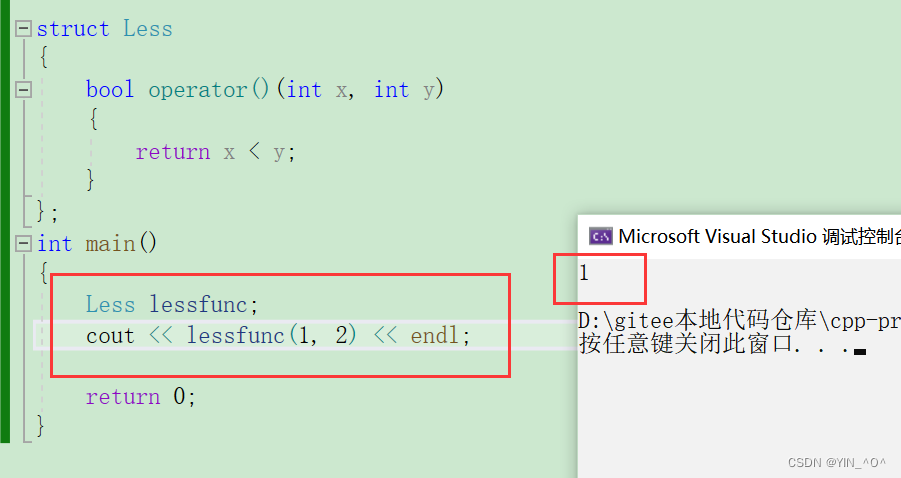
我们来写一个判断小于的仿函数,怎么做呢?
定义一个类,重载一下()就行了,函数体的实现根据我们的需求去写:
ps:也可以用class,区别只是它的的默认访问限定符不同。
那我们来用一下这个仿函数:
1小于2为真,所以打印结果为1。
🆗,那如果我们只看这一行:
这是不是就像是一个函数调用啊。
当然它本质是去调用了类里面的operator()。
那要告诉大家的是仿函数它的作用和价值还是很大的,不过我们现在还不能很好的体会到。
C++其实本质搞出这个东西是因为函数指针太复杂了,而仿函数在很多场景能达到一个替代函数指针的作用。
就比如我们这里优先级队列控制这个大堆小堆,我们之前实现过堆,我们知道控制大堆小堆其实就是就是控制里面元素的比较方式不同。
那我们C语言解决这样的问题是不是就是去传一个函数指针嘛,就比如C语言里面那个qsort函数:
它是不是就是通过传递一个函数指针来控制元素的比较方式啊。
而C++的sort就可以传仿函数去控制:
当然不是只能传仿函数,我们看到它给的是一个模板。
那我们上面用到的greater包括默认给的less其实就是库里面提供的仿函数。
当然我们看到它可以写成这样
greater<int>,那库里面的其实是实现成模板了。
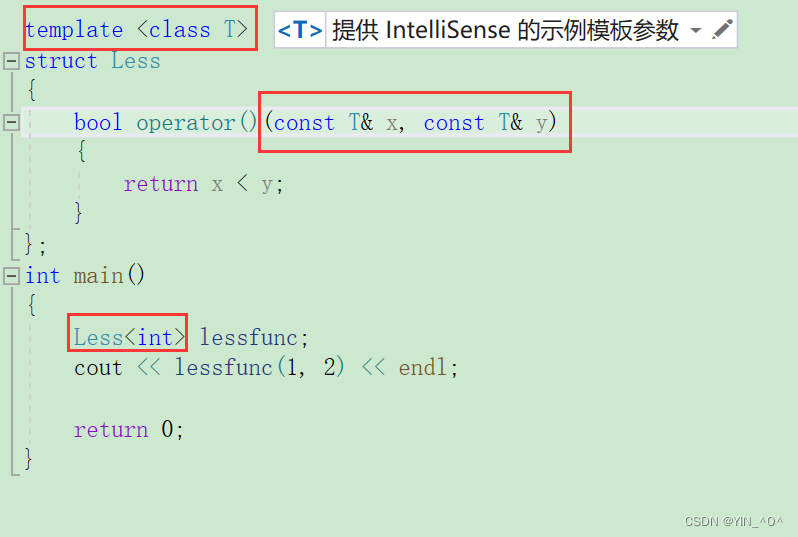
而我们刚才这样写的是只针对整型,如果像比较任意类型我们就可以将他实现成模板:
1.2.2 在OJ中的使用:数组中的第K个最大元素
下面我们来看一个题:数组中的第K个最大元素
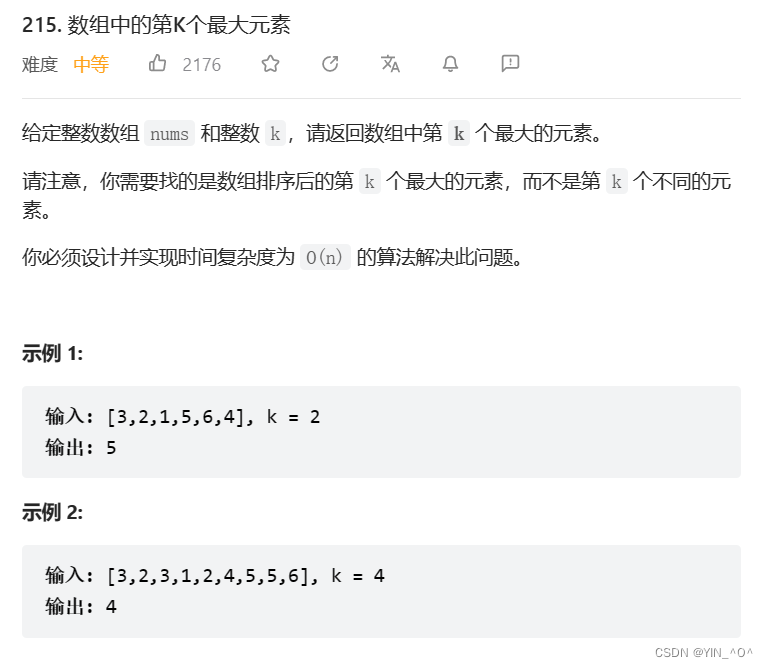
思路1:排序
那这道题我们最容易想到的方法应该就是堆数组排个序,如果数组是有序的,那我们想拿到第k个最大的元素,不是轻而易举嘛。
那直接用sort排序就行了,要注意sort默认是升序。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
sort(nums.begin(),nums.end());
return nums[nums.size()-k];
}
};
但是题目要求时间复杂度为 O(n) ,那我们还有没有其它更好的算法呢?
思路2:priority_queue
🆗,我们是不是可以考虑使用优先级队列(堆)来搞啊。
那我们现在要使用优先级队列的话,还需要自己写吗?
是不是可以直接用啊——priority_queue。
怎么做呢?
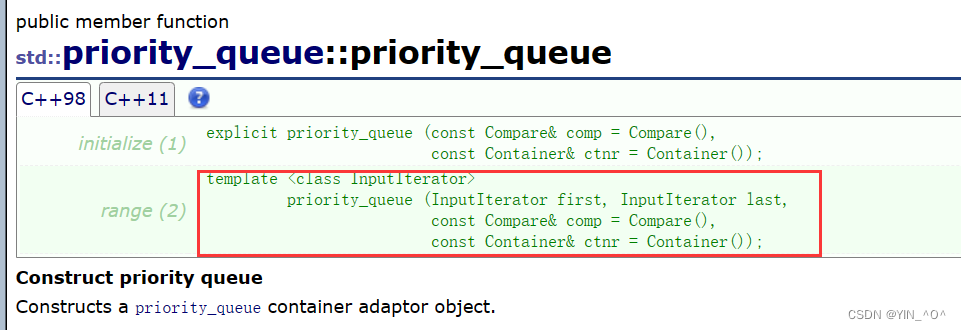
那我们知道它默认是大堆,那我们就用大堆,首先我们拿数组的数据建堆,怎么建?
我们可以选择这个迭代器区间的这个构造函数。
拿建好堆之后,默认是大堆,那我们就可以pop k-1次,然后堆顶的那个数据不就是第K个最大的数了嘛。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int> q(nums.begin(),nums.end());
while(--k)
{
q.pop();
}
return q.top();
}
};
那这种写法的时间复杂度应该是多少呢?
🆗,应该是O(N+k*logN),大家可以自己算一下,这里建堆包括pop的时间复杂度我们之前二叉树的文章也讲过。
那还要其它方法吗?
思路3:TOP-K思想
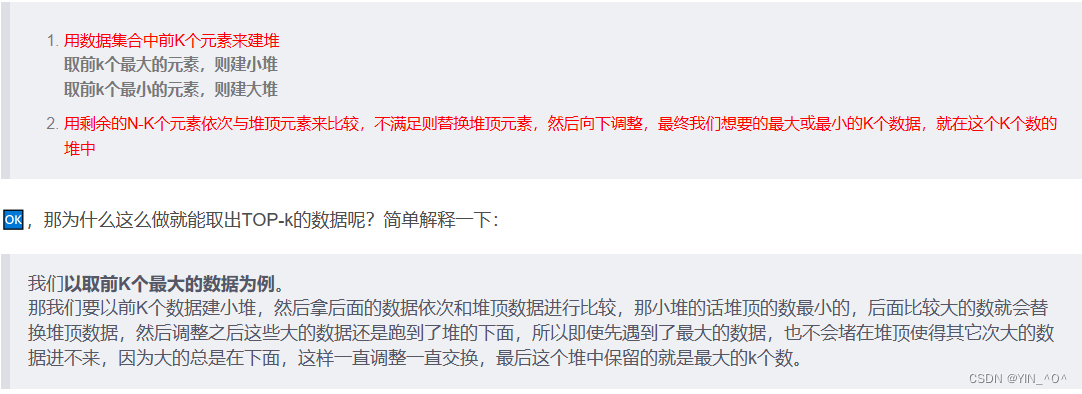
我们还可以考虑用TOP-K的思想去解决这道题:
首先我们来复习一下TOP-K(时间复杂度是O(N*log2K))的思想,这也是我们之前文章讲过的内容:
那这道题我们可以怎么做呢?
我们是不是可以先拿前K个数建堆,这里我们想要获取最大得前K个,应该建小堆,然后一个个比较,不符合大小关系就调整,最终堆中得数据就是最大的前K个,那此时堆顶得数据不就是我们要的数嘛。
当然我们现在用的是库里面的priority_queue,没有向下调整这些接口,而且top返回的也是引用,也不能直接替换堆顶数据,所以我们可以先pop,然后再push。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
//建小堆
priority_queue<int,vector<int>,greater<int>> q(nums.begin(),nums.begin()+k);
for(size_t i=k;i<nums.size();++i)
{
if(nums[i]>q.top())
{
q.pop();
q.push(nums[i]);
}
}
return q.top();
}
};
2. priority_queue的模拟实现
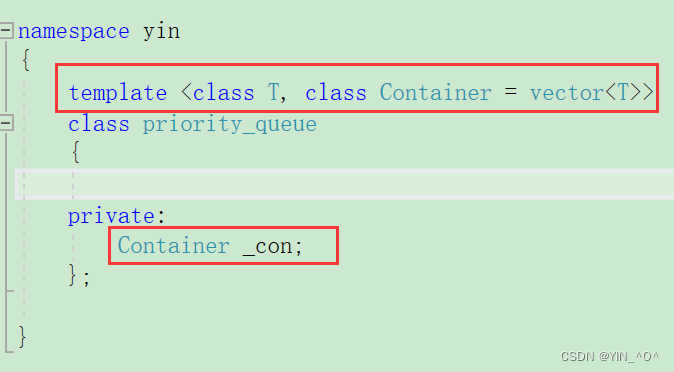
那我们接下来就对priority_queue进行一个模拟实现:
那我们还是按照库里面的来,把它实现成一个容器适配器的类模板
那它的结构就是这样的,第三个模板参数即比较的仿函数我们放到后面再搞。
2.1 核心接口
然后先我们来实现一下它的几个核心的接口:
首先写一下push:
那我们再来复习一下,堆的push怎么搞的?
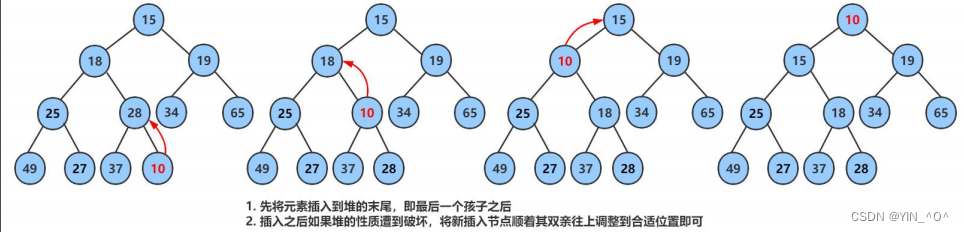
🆗,堆的逻辑结构是一个完全二叉树,其物理结构,即底层实际的存储结构是一个一维数组(我们这里使用的是vector),我们push的时候先尾插一个数据,然后是不是要对它进行向上调整啊,确保插入新数据之后它还是一个堆。
那我们待会还要实现一下向上调整。
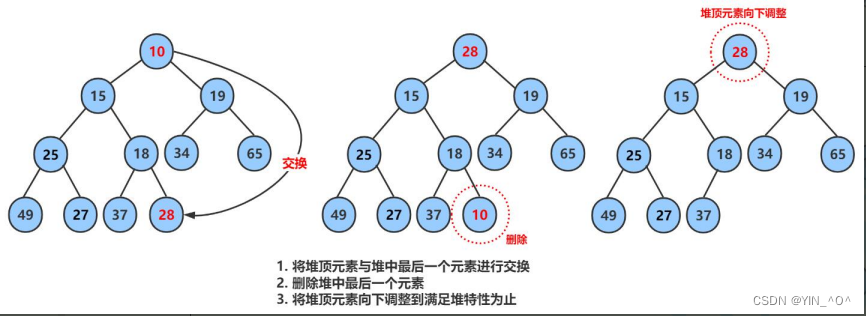
然后pop,再来回忆一下,堆的删除怎么搞?
🆗,是不是将堆顶的数据跟最后一个数据进行交换,然后删除数组最后一个数据,再进行向下调整啊。
当然待会我们也要写一下向下调整。
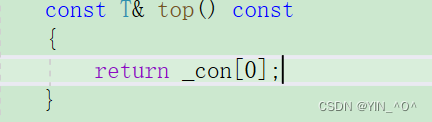
然后top,那就简单了:
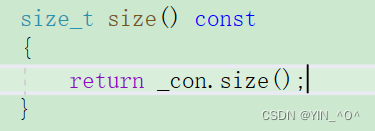
然后还有size:
empty:
然后我们回过头来把向上调整实现一下。
2.2 向上调整
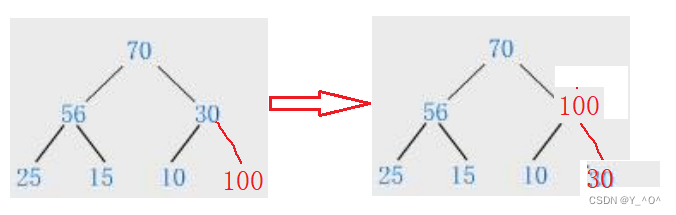
向上调整怎么搞(这里我们默认先按大堆来搞),回忆一下:
怎么调?
首先进行向上调整要保证之前的数据必须是一个堆。
然后看插入的数据满足不满足对应的大小关系,不满足就进行交换,直到满足为止。
100这个结点是不是大于它的父亲啊,那大堆中大的才应该做父亲,所以呢,就应该交换100和30这两个结点。
那调整一次就完了吗?
如果调整一次后满足了,那确实就结束了,但是现在是不是还不满足是一个大堆啊,那就要继续调整。
100还是大于它的父亲70:
所以:
这个调整应该是一个循环的过程,那循环什么时候结束呢?
当调整到所有结点都满足大堆或小堆的关系时,或者需要一直调整,当插入的新数据一直交换到成为根结点时就结束了。
当然如果插入的数据直接满足,那一次也不需要调整。
我们把这种从下往上调整的算法叫做向上调整。
思路还是和我们之前讲的一样。
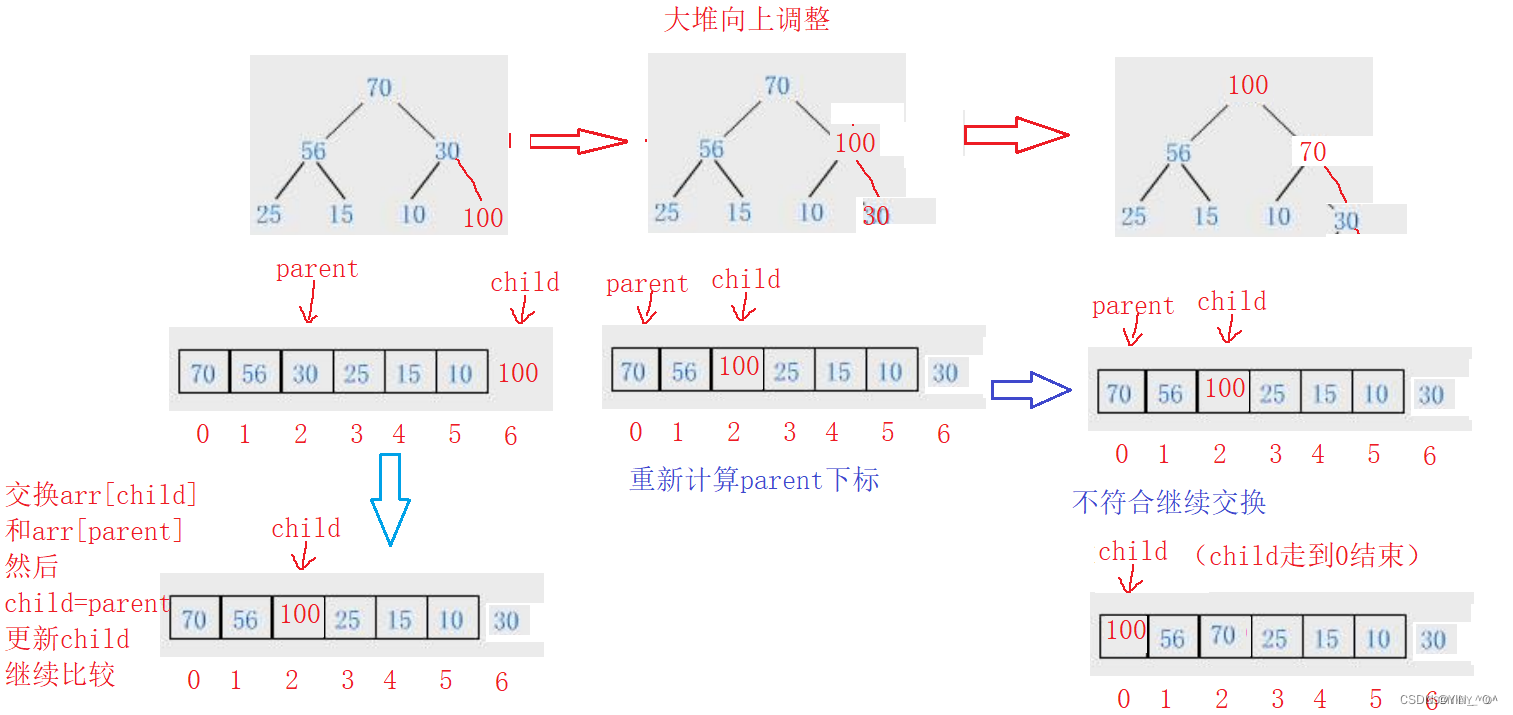
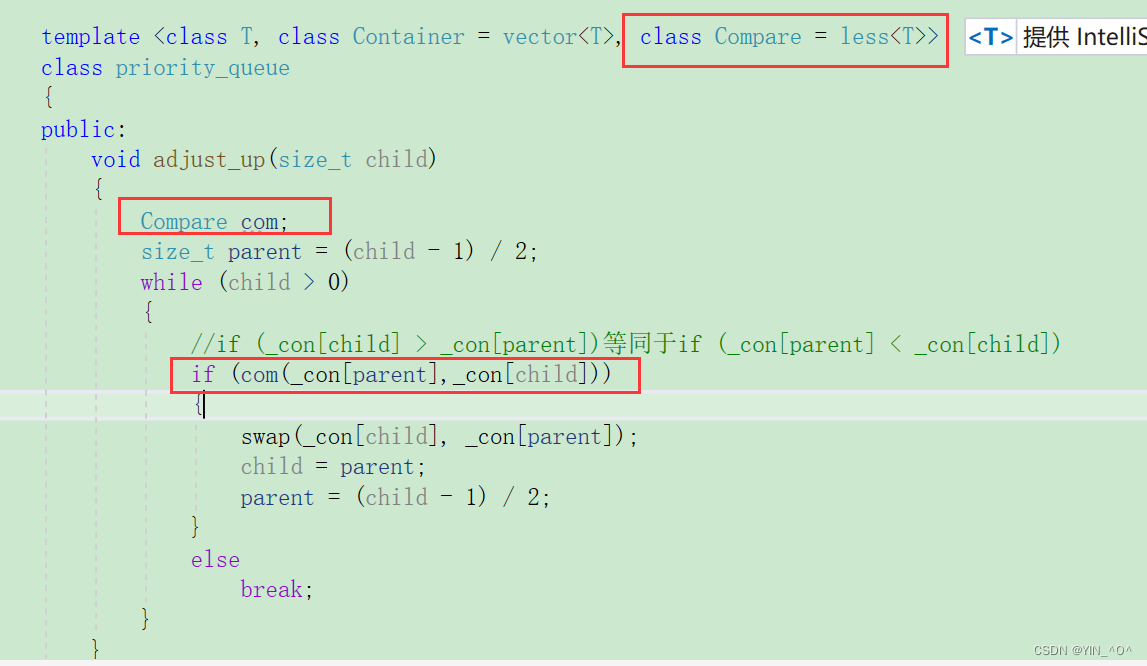
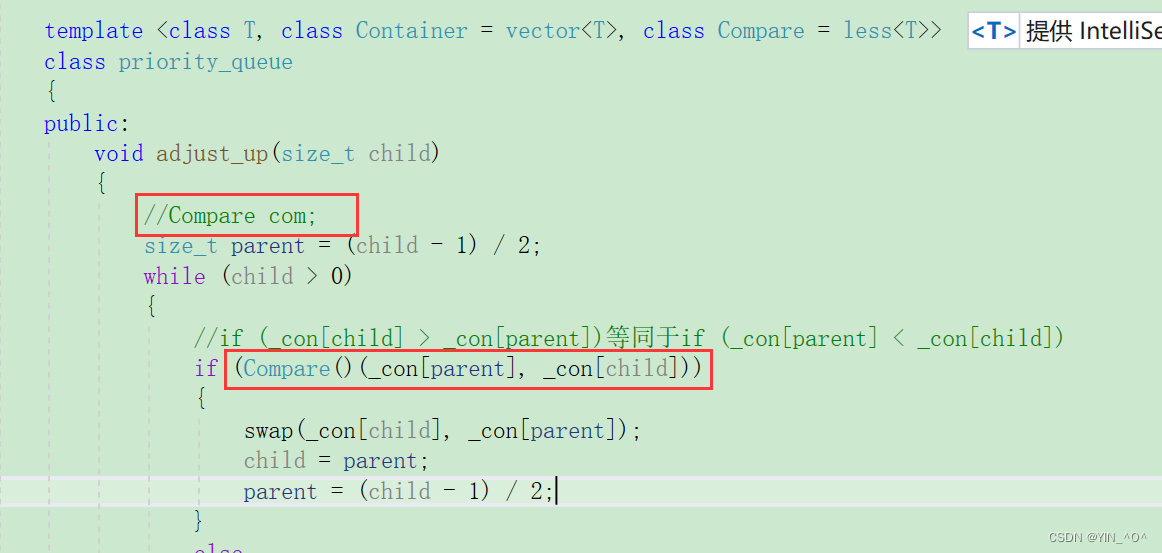
void adjust_up(size_t child)
{
size_t parent = (child - 1) / 2;
while (child > 0)
{
if (_con[child] > _con[parent])
{
swap(_con[child], _con[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}
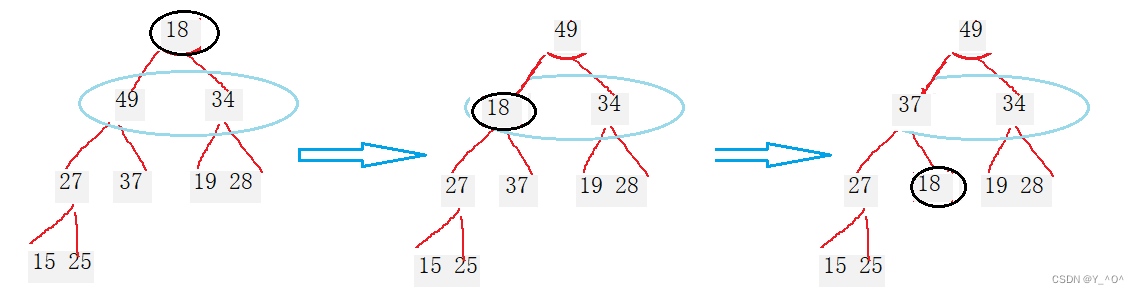
2.3 向下调整
然后向下调整呢?
如何调整:
其实思路跟向上调整一样,只不过这次我们是从上往下,不符合关系的进行交换,直至使它成为一个新的大堆。
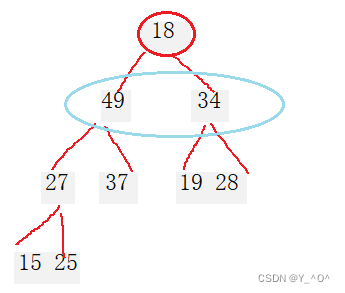
我们开始调整:
18在这里肯定不合适,它比自己的孩子还要小,所以要交换。
和谁交换?
34可以吗,34换到堆顶,它是不是还撑不住啊。
所以我们要选择它的孩子中大的那一个进行交换。
那在这里就是49。
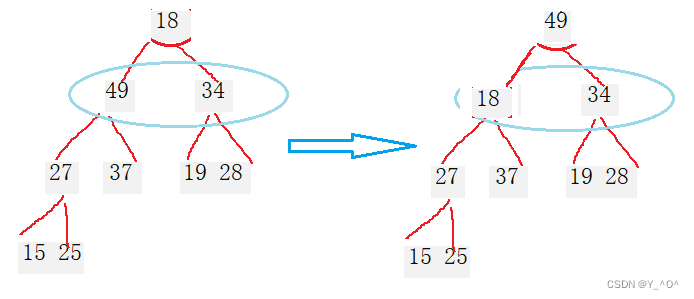
那现在18坐到原来49的位置,现在这个位置怎么样?
🆗,18是不是还是坐不稳啊。
还得进行交换。
选择18的孩子中大的那一个交换:
现在是不是就可以了啊。
我们交换了两次完成了,所以这还是一个循环的过程。
那这个循环的交换过程应该什么时候停止?
是不是当交换到满足大小关系或者一直交换,直到自己成为叶子结点时结束啊。
void adjust_down(size_t parent)
{
size_t child = parent * 2 + 1;
while (child < _con.size())
{
//得出较大(小堆则较小)的那个孩子
if (child + 1 < _con.size()
&& _con[child] < _con[child + 1])
child++;
if (_con[parent] < _con[child])
{
swap(_con[parent], _con[child]);
parent = child;
child = parent * 2 + 1;
}
else
break;
}
}
那我们来测试一下我们写的priority_queue:
没问题。
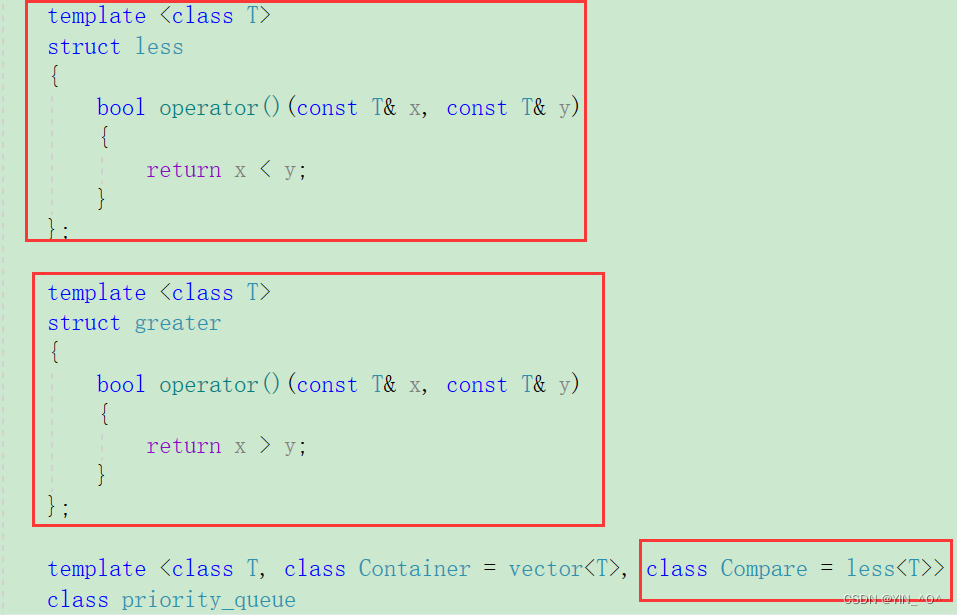
2.4 仿函数less和greater模拟实现及使用
那然后呢我们把第三个模板参数加上,把仿函数实现一下:
我们刚才实现的是大堆,那我们想要小堆怎么办?
我们之前数据结构学习堆的时候就知道了,是不是把向上向下调整里面的比较的大于号换成小于就行了啊
但是,经过我们上面的学习以及对仿函数的介绍,我们是不是可以通过传仿函数去控制啊。
所以我们要增加一个模板参数,然后通过两个仿函数去控制比较大于还是比较小于,以此控制大堆还是小堆。
那怎么使用第三个参数呢?
我们这里和库里面保持一样,默认第三个参数class Compare的缺省值是仿函数less,对应的是大堆。
那这样做就可以了:
那这下我们就可以通过仿函数去控制大小堆 了。
来试一下:
现在默认用less是大堆:
那想要小堆怎么办?用greater就行了:
🆗,就好了,大家理解一下这个过程:
当然也可以这样写
就是用匿名对象嘛。
3. priority_queue 存放自定义类型数据
下面我们再来研究一个问题:
class Date
{
public:
Date(int year = 1900, int month = 1, int day = 1)
: _year(year)
, _month(month)
, _day(day)
{}
bool operator<(const Date& d)const
{
return (_year < d._year) ||
(_year == d._year && _month < d._month) ||
(_year == d._year && _month == d._month && _day < d._day);
}
bool operator>(const Date& d)const
{
return (_year > d._year) ||
(_year == d._year && _month > d._month) ||
(_year == d._year && _month == d._month && _day > d._day);
}
friend ostream& operator<<(ostream& _cout, const Date& d);
private:
int _year;
int _month;
int _day;
};
ostream& operator<<(ostream& _cout, const Date& d)
{
_cout << d._year << "-" << d._month << "-" << d._day;
return _cout;
}
现在有一个日期类,并重载了
<<,>和<。
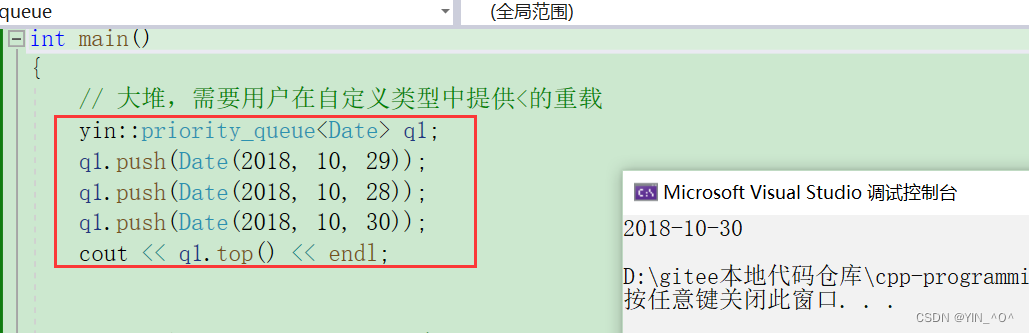
那现在呢,我想用我们的priority_queue(优先级队列)去存我们的自定义类型数据——日期类的变量,可以吗?
我们来试一下:
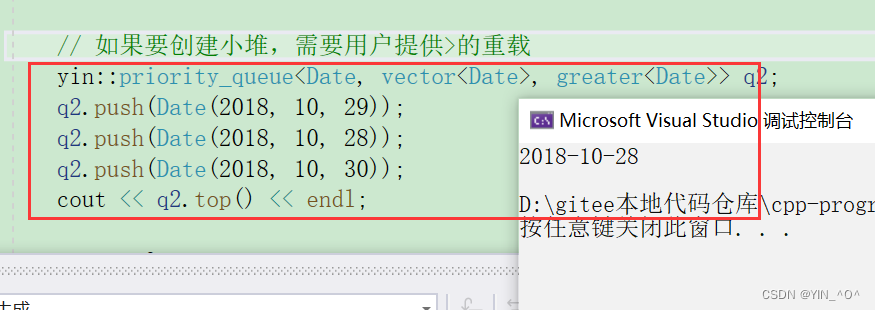
没问题,可以,现在默认是大堆嘛,所以top是最大的那个日期。
如果换成小堆:
那堆顶就是最小的。
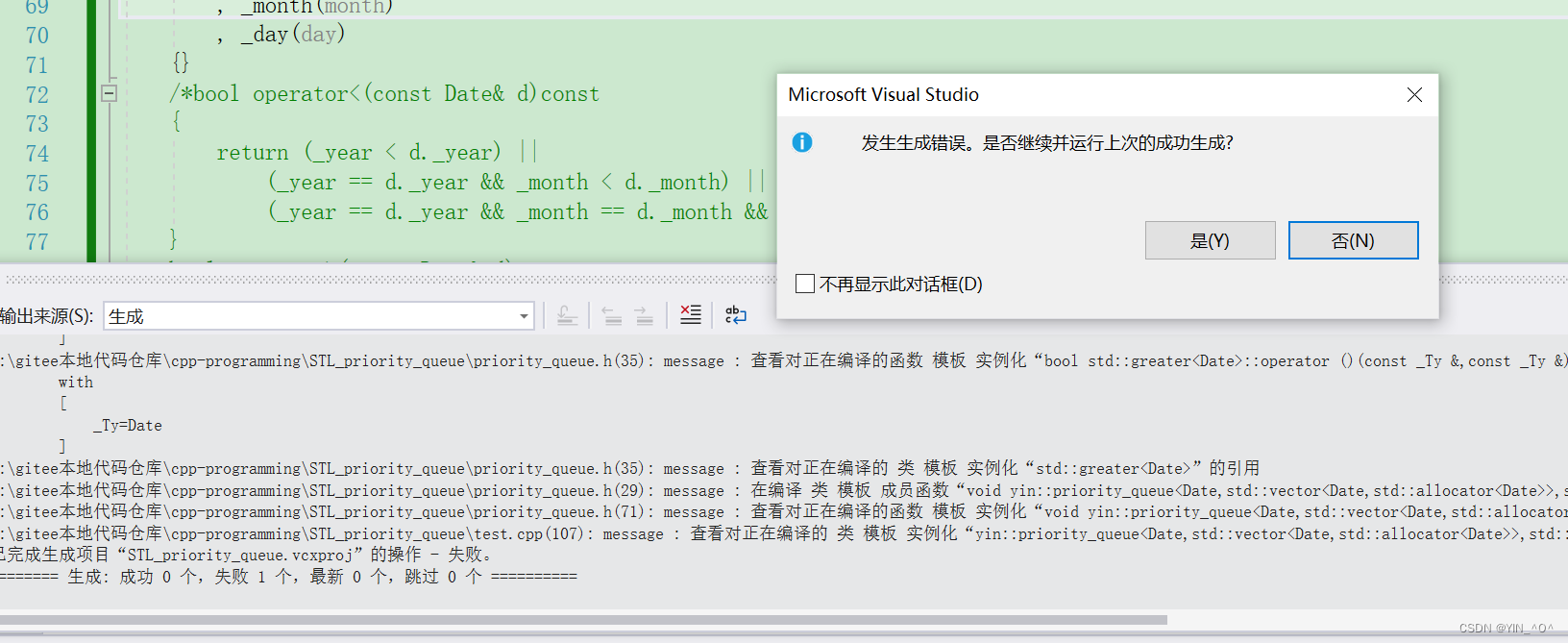
那这里为什么可以,其实是因为我们的日期类重载了>和<,因为它里面建堆的过程是不是要进行比较啊。
如果没有>和<的重载就不行了。
所以:
如果在priority_queue中放自定义类型的数据,用户需要在自定义类型中提供> 或者< 的重载
4. 拓展
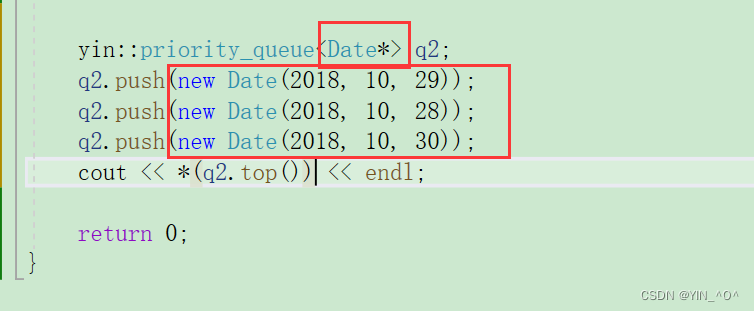
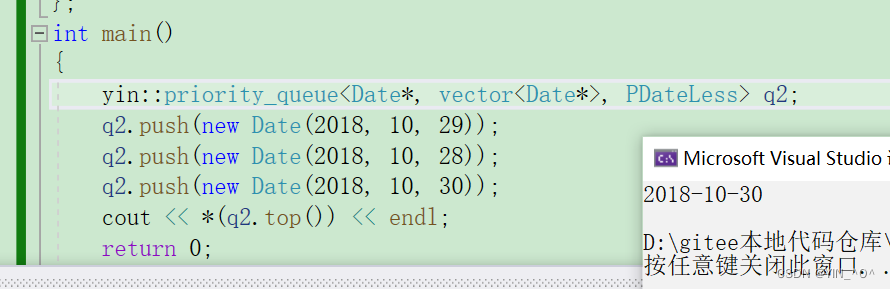
🆗,再来看,如果是这样呢:
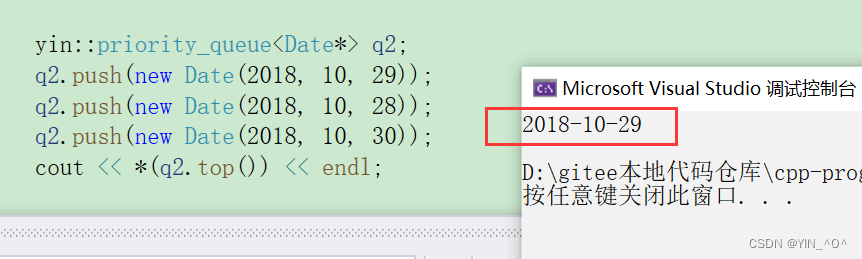
现在它里面存的是Date* 的指针,我们来看下结果:
好像没什么问题,不过结果好像不对。
而且:
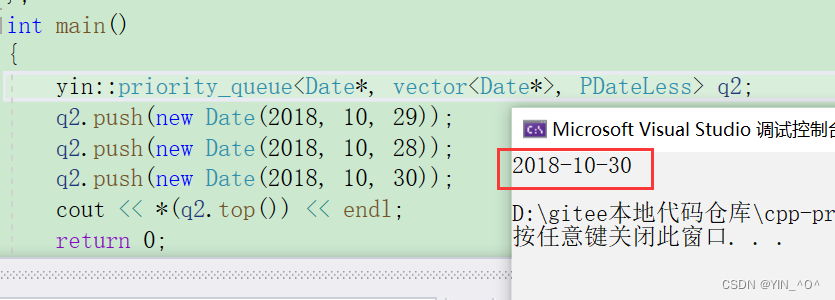
我们重新编译一下,再运行
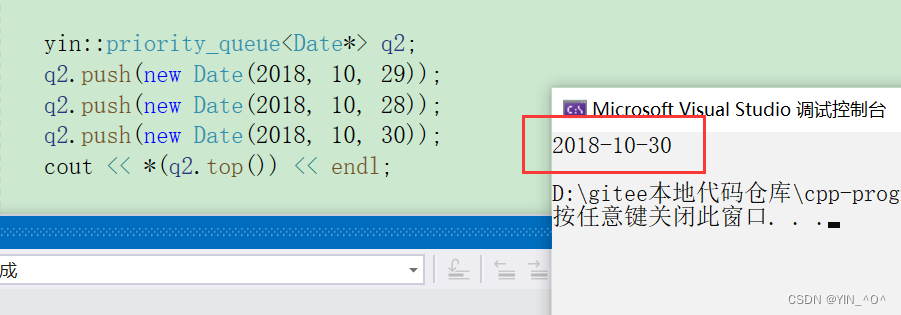
哎呀,怎么回事。
怎么结果会变化啊,为什么呢?
🆗,原因在于:
我们现在里面存的是啥,是Date* 的指针变量,那指针能比较大小嘛?
当然也可以,它是内置类型,指针比较大小的话就是去比较对应地址的大小嘛。
但是这里我们new出来的地址,它们的大小关系可认为是随机的,所以虽然可以比,但是这结果是我们想要的嘛,是不是不是啊。
我们想要的的是不是去比较它们指针指向的Date类对象的大小啊。
指针是内置类型,我们也没法重载它的比较操作,那怎么办呢?
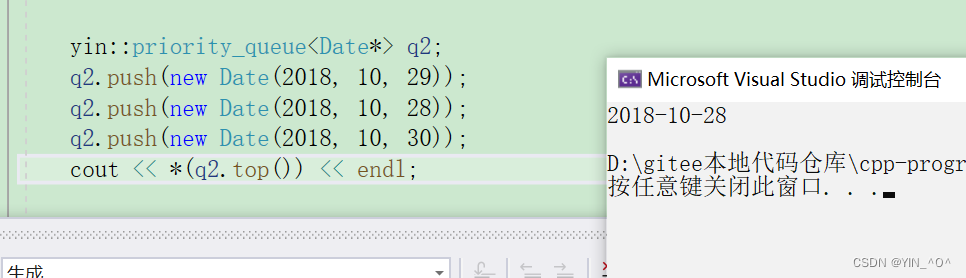
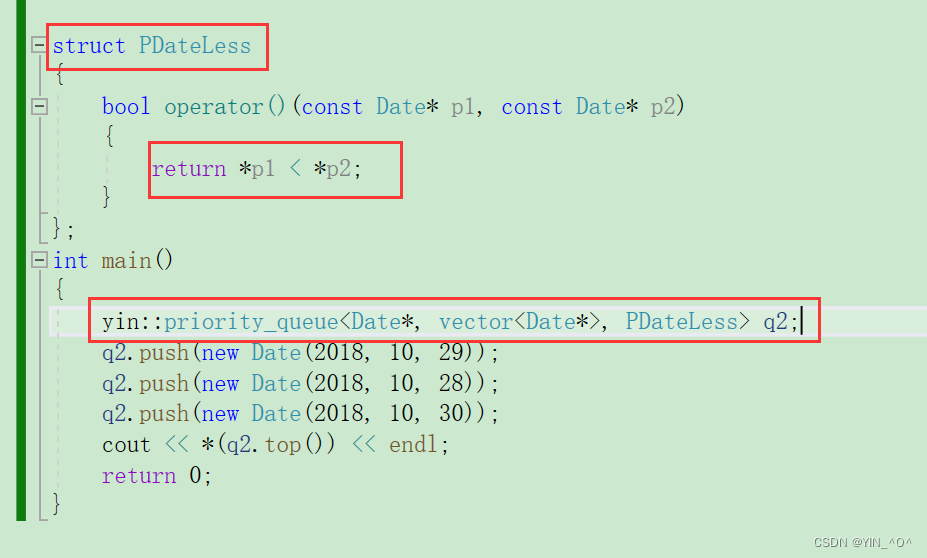
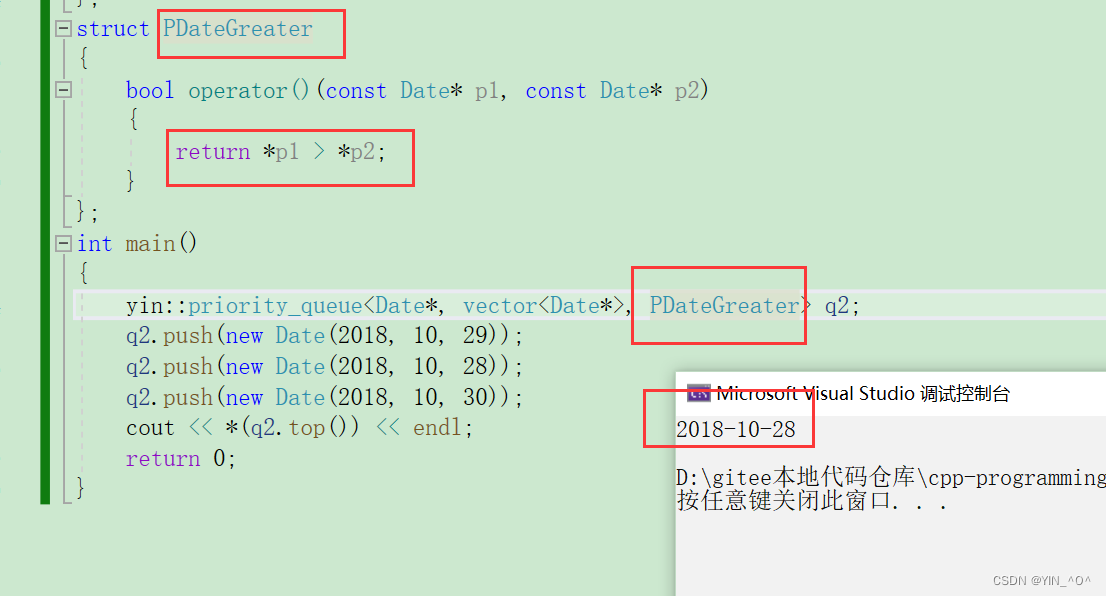
我们是不是可以使用仿函数来解决啊。
然后我们再运行:
就会发现结果正确并且不会变化了。
那如果要小堆,很简单,再搞一个仿函数:
就可以了。
所以这里我们看到有了仿函数,即使是内置类型,这里我们也可以去控制它的比较方式。
这篇文章的内容就先到这里,欢迎大家指正!!!























![[Nginx 发布项目] 打包后的项目,使用nginx发布](https://img-blog.csdnimg.cn/45bc9b3e282e44f683b3b5ab1499e5c7.png)