文章目录
- 第五章 贝叶斯分类与概率图模型
- 5.1、贝叶斯决策与贝叶斯分类
- 5.1.1、贝叶斯基本原理
- 5.1.2、朴素贝叶斯分类器(naive bayes)
- 5.1.3、半朴素贝叶斯
- 5.2、有向图与无向图一般概念
- 5.2.1、有向图
- 5.2.2、无向图
- 5.2.3、条件独立性
- 5.2.4、图模型推理的概念
- 5.3、马尔可夫随机场
- 5.3.1、基本概念
- 5.3.2、应用
- 5.4、隐马尔可夫模型
- 5.4.1、引例
- 5.4.2、组成要素
- 5.4.3、基本问题
第五章 贝叶斯分类与概率图模型
5.1、贝叶斯决策与贝叶斯分类
5.1.1、贝叶斯基本原理
用于生成式模型(y取不同值有不同概率)
p
(
y
∣
x
)
=
p
(
x
,
y
)
p
(
x
)
=
p
(
x
∣
y
)
p
(
y
)
p
(
x
)
p(y|\boldsymbol x)=\dfrac{p(\boldsymbol x,y)}{p(\boldsymbol x)}=\dfrac{p(\boldsymbol x| y)p(y)}{p(\boldsymbol x)}
p(y∣x)=p(x)p(x,y)=p(x)p(x∣y)p(y)
5.1.2、朴素贝叶斯分类器(naive bayes)
主要假设:各特征之间相互独立且权重相同
对于上面的表达式,其中的 x \boldsymbol x x可表示为: x = ( x 1 , x 2 , x 3 , … , x n ) \boldsymbol x=\left(x_1,x_2,x_3,\ldots,x_n\right) x=(x1,x2,x3,…,xn)
由于各个
x
x
x间是独立的,因此上述表达式可写成:
P
(
y
∣
x
1
,
…
,
x
n
)
=
P
(
x
1
∣
y
)
P
(
x
2
∣
y
)
.
.
.
P
(
x
n
∣
y
)
P
(
y
)
P
(
x
1
)
P
(
x
2
)
.
.
.
P
(
x
n
)
即:
P
(
y
∣
x
1
,
…
,
x
n
)
=
P
(
y
)
Π
i
=
1
n
P
(
x
i
∣
y
)
P
(
x
1
)
P
(
x
2
)
…
P
(
x
n
)
P(y|x_1,\ldots,x_n)=\dfrac{P(x_1|y)P(x_2|y)...P(x_n|y)P(y)}{P(x_1)P(x_2)...P(x_n)}\\即:P(y|x_1,\ldots,x_n)=\dfrac{P(y)\Pi_{i=1}^nP(x_i|y)}{P(x_1)P(x_2)\ldots P(x_n)}
P(y∣x1,…,xn)=P(x1)P(x2)...P(xn)P(x1∣y)P(x2∣y)...P(xn∣y)P(y)即:P(y∣x1,…,xn)=P(x1)P(x2)…P(xn)P(y)Πi=1nP(xi∣y)
-
当属性是离散型时:类的先验概率可通过训练集中各类样本出现的次数来估计:
p ( x i ∣ y ) = ∣ D y , x i ∣ ∣ D y ∣ p(x_i|y)=\dfrac{|D_{y,x_i}|}{|D_y|} p(xi∣y)=∣Dy∣∣Dy,xi∣
其中 D y D_y Dy表示训练集 D D D中 y y y类样本组成的集合, D y , x i D_{y,x_i} Dy,xi是 D y D_y Dy在第 i i i个属性上取值为 x i x_i xi的样本组成的集合。 -
当属性是连续型时:可假设变量服从某种概率分布
例如是高斯朴素贝叶斯分类器,则条件概率函数可以写成:
p
(
x
i
∣
y
)
=
1
2
π
σ
y
,
i
exp
{
−
1
2
σ
y
,
i
2
(
x
i
−
μ
y
,
i
)
2
}
p(x_i|y)=\frac{1}{\sqrt{2\pi}\sigma_{y,i}}\exp\{-\frac{1}{2\sigma_{y,i}^2}(x_i-\mu_{y,i})^2\}
p(xi∣y)=2πσy,i1exp{−2σy,i21(xi−μy,i)2}
μ y , i \mu_{y,i} μy,i:在类别为𝑦的样本中,特征𝑥_𝑖的均值
σ y , i \sigma_{y,i} σy,i:在类别为𝑦的样本中,特征𝑥_𝑖的标准差
参考自:
朴素贝叶斯分类器(Naive Bayes Classifiers)_K.Sun的博客-CSDN博客
高斯朴素贝叶斯(Gaussian Naive Bayes)原理与实现——垃圾邮件识别实战 - ISGuXing - 博客园 (cnblogs.com)
栗:
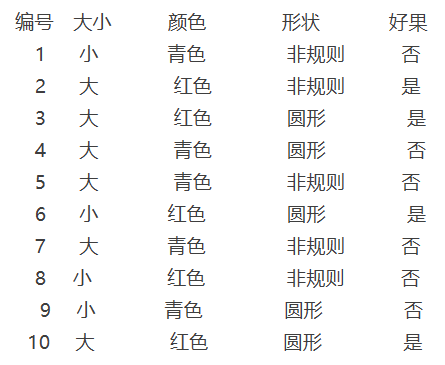
现在在超市我正要买的一个苹果的特征如下:
大小 颜色 形状 好果
大 红色 圆形 ?
P
(
y
∣
x
1
,
x
2
,
x
3
)
=
P
(
x
1
∣
y
)
P
(
x
2
∣
y
)
P
(
x
3
∣
y
)
P
(
y
)
P
(
x
1
)
P
(
x
2
)
P
(
x
3
)
P(y|x_1,x_2,x_3)=\dfrac{P(x_1|y)P(x_2|y)P(x_3|y)P(y)}{P(x_1)P(x_2)P(x_3)}
P(y∣x1,x2,x3)=P(x1)P(x2)P(x3)P(x1∣y)P(x2∣y)P(x3∣y)P(y)
其中:
p
(
y
=
好果
)
=
4
/
10
,
p
(
y
=
一般
)
=
6
/
10
p(y=好果)=4/10,p(y=一般)=6/10
p(y=好果)=4/10,p(y=一般)=6/10,
p
(
x
1
=
大
∣
c
=
好果
)
=
3
/
4
,
P
(
x
2
=
红色
∣
c
=
好果
)
=
4
/
4
,
p
(
x
3
=
圆形
∣
c
=
好果
)
=
3
/
4
p
(
x
1
=
大
∣
c
=
一般
)
=
3
/
6
,
P
(
x
2
=
红色
∣
c
=
一般
)
=
1
/
6
,
p
(
x
3
=
圆形
∣
c
=
一般
)
=
2
/
6
p(x_1=大|c=好果)=3/4,P(x_2=红色|c=好果)=4/4,p(x_3=圆形|c=好果)=3/4\\ p(x_1=大|c=一般)=3/6,P(x_2=红色|c=一般)=1/6,p(x_3=圆形|c=一般)=2/6
p(x1=大∣c=好果)=3/4,P(x2=红色∣c=好果)=4/4,p(x3=圆形∣c=好果)=3/4p(x1=大∣c=一般)=3/6,P(x2=红色∣c=一般)=1/6,p(x3=圆形∣c=一般)=2/6
其实我们只需要比较:
p
(
y
=
好果
∣
x
)
和
p
(
y
=
一般
∣
x
)
p(y=好果|\mathbf{x})和p(y=一般|\mathbf{x})
p(y=好果∣x)和p(y=一般∣x)的大小,而分母
P
(
x
1
)
P
(
x
2
)
P
(
x
3
)
P(x_1)P(x_2)P(x_3)
P(x1)P(x2)P(x3)是一样的,所以可以只算分子。
p
(
y
=
好果
∣
x
)
∝
p
(
y
=
好果
)
∗
p
(
x
1
=
大
∣
c
=
好果
)
∗
P
(
x
2
=
红色
∣
c
=
好果
)
∗
p
(
x
3
=
圆形
∣
c
=
好果
)
=
4
/
10
∗
3
/
4
∗
4
/
4
∗
3
/
4
=
0.225
p
(
y
=
一般
∣
x
)
∝
6
/
10
∗
3
/
6
∗
1
/
6
∗
2
/
6
=
0.0167
p(y=好果|\mathbf{x}) \propto p(y=好果)*p(x_1=大|c=好果)*P(x_2=红色|c=好果)*p(x_3=圆形|c=好果)\\ =4/10 * 3/4 * 4/4 * 3/4 =0.225\\ p(y=一般|\mathbf{x}) \propto 6/10 * 3/6 * 1/6 * 2/6= 0.0167
p(y=好果∣x)∝p(y=好果)∗p(x1=大∣c=好果)∗P(x2=红色∣c=好果)∗p(x3=圆形∣c=好果)=4/10∗3/4∗4/4∗3/4=0.225p(y=一般∣x)∝6/10∗3/6∗1/6∗2/6=0.0167
所以这个苹果是好果。
参考:朴素贝叶斯分类器:例子解释 (qq.com)
某个样本的属性值并未出现在训练集中,导致尽管要预测的这个苹果看起来很像是好果,但是朴素贝叶斯目标函数的结果仍为0,最终被划分为一般的苹果。这需要拉普拉斯修正朴素贝叶斯分类:拉普拉斯修正。仅做了解
5.1.3、半朴素贝叶斯
朴素贝叶斯分类器的一个重要假定:分类对应的各个属性间是相互独立的,然而在现实应用中,这个往往难以做到,那怎么办呢?
很简单,适当考虑一部分属性间的相互依赖关系,这种放松后的分类称为半朴素贝叶斯分类,其中最常用的策略:假定每个属性仅依赖于其他最多一个属性,称其依赖的这个属性为其超父属性,这种关系称为:独依赖估计(ODE)。因此表达式变为:
p
(
y
∣
x
)
∝
p
(
y
)
∏
i
=
1
d
p
(
x
i
∣
y
,
p
a
r
i
)
p(y|\mathbf{x})\propto p(y)\prod\limits_{i=1}^d p(x_i|y,par_i)
p(y∣x)∝p(y)i=1∏dp(xi∣y,pari)
其中,
p
a
r
i
par_i
pari为属性
x
i
x_i
xi依赖的属性,称为
x
i
x_i
xi的父属性。
参考自: 机器学习:半朴素贝叶斯分类器_算法channel的博客-CSDN博客
5.2、有向图与无向图一般概念
概率图分为有向图和无向图两大类。有向图模型也就是贝叶斯网络,图之间的链接有一个特定的方向,使用箭头表示。另一大类是马尔科夫随机场,也被称为无向图模型,这个模型中,链接没有箭头,没有方向性质。有向图对于表达随机变量之间的因果关系很有用,而无向图对于表示随机变量之间的软限制比较有用。为了求解推断问题,通常比较方便的做法是把有向图和无向图都转化为一个不同的表示形式,被称为因子图。
5.2.1、有向图
有向图中的边有明确的由一个节点到另一个节点的方向,也称作贝叶斯网络
一个有向图中所有变量的联合分布为每个节点以其所有父节点为条件的概率分布乘积:
p
(
x
1
,
…
,
x
K
)
=
∏
k
=
1
K
p
(
x
k
∣
p
a
r
(
x
k
)
)
p(x_1,\ldots,x_K)=\prod\limits_{k=1}^K p(x_k\mid par(x_k))
p(x1,…,xK)=k=1∏Kp(xk∣par(xk))
与一般化表达
p
(
x
1
,
.
.
.
,
x
K
)
=
p
(
x
K
∣
x
1
,
.
.
.
,
x
K
−
1
)
…
p
(
x
2
∣
x
1
)
p
(
x
1
)
p(x_1,...,x_K)=p(x_K|x_1,...,x_{K-1})\dots p(x_2|x_1)p(x_1)
p(x1,...,xK)=p(xK∣x1,...,xK−1)…p(x2∣x1)p(x1)的区别:
一般表达是由概率原则得到的任何情况都正确的分解表达,其假设所有变量之间都有关系;有向图表达是在某种具体图结构下的表达,其在不同变量之间引入了独立性假设。
例1:

p ( x 1 , . . . , x 7 ) = p ( x 1 ) p ( x 2 ) p ( x 3 ) p ( x 4 ∣ x 1 , x 2 , x 3 ) ⋅ p ( x 5 ∣ x 1 , x 3 ) p ( x 6 ∣ x 4 ) p ( x 7 ∣ x 4 , x 5 ) p(x_1,...,x_7)=p(x_1)p(x_2)p(x_3)p(x_4|x_1,x_2,x_3)\\ \cdot p(x_5|x_1,x_3)p(x_6|x_4)p(x_7|x_4,x_5) p(x1,...,x7)=p(x1)p(x2)p(x3)p(x4∣x1,x2,x3)⋅p(x5∣x1,x3)p(x6∣x4)p(x7∣x4,x5)
例2:(注意初始分布和视频帧的使用)
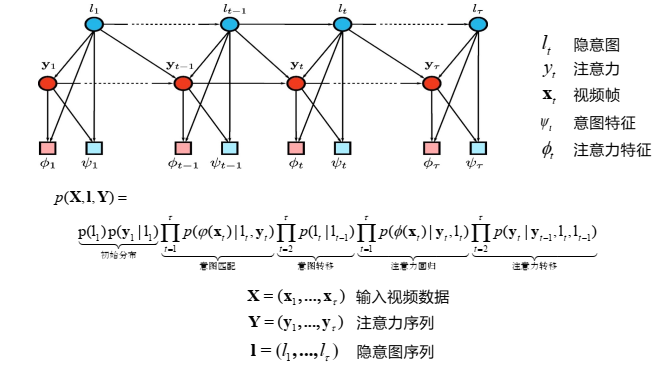
5.2.2、无向图
无向图中连接节点的边没有方向,也称作马尔可夫随机场(Markov Random Field)
一个团是图中一个全连接的结点子集,团中任意两个结点间都有边相连接。 一个 最大团是一个不能再增加结点的团,最小的团就是图中一条边连接的两个结点组成的团。

一个无向图总是可以划分为很多个团的集合。同一个团中的结点绝对不满足条件独立性, 而不同团之间的结点是可以有条件独立性的。这里我们就用将联合概率密度分解成定义在团上的局部函数的乘积,我们将这个局部函数称为势函数(potential function)。(结合后面图像去噪的例子来看)
p
(
x
)
∝
∏
C
∈
e
ψ
x
C
(
x
C
)
=
1
Z
∏
C
∈
e
ψ
x
C
(
x
C
)
\begin{array}{c}p(\mathbf{x})\propto\prod\limits_{C\in e}\psi_{\mathbf{x}_C}\left(\mathbf{x}_C\right)\\ =\dfrac{1}{Z}\prod\limits_{C\in e}\psi_{\mathbf{x}_C}\left(\mathbf{x}_C\right)\end{array}
p(x)∝C∈e∏ψxC(xC)=Z1C∈e∏ψxC(xC)
其中
e
e
e是所有最大团的集合,团
C
C
C中的变量集合为
x
C
\mathbf x_C
xC,其中:
Z
=
∑
x
∏
C
∈
e
ψ
x
C
(
x
C
)
Z=\sum_{\mathbf{x}}\prod\limits_{C\in e}\psi_{\mathbf{x}_C}\left(\mathbf{x}_C\right)
Z=x∑C∈e∏ψxC(xC)
在实际使用中,我们可以将势函数表示成:
ψ
C
(
x
C
)
=
exp
{
−
E
(
x
C
)
}
\psi_{C}(\boldsymbol{x}_{C})=\exp\{-E(\boldsymbol{x}_{C})\}
ψC(xC)=exp{−E(xC)},其中的
E
(
x
C
)
E(\boldsymbol{x}_{C})
E(xC)称作能量函数,该指数表达式称为玻尔兹曼分布,这样可以把势函数的积转化成每个最大团 能量的和。
《概率图模型:原理与技术》里面讲的更为细致,目前简单理解为用因子的乘积去表示联合概率,而为了使因子数量最少,所以选用最大团。
5.2.3、条件独立性
基本表示:
-
两个随机变量相互独立(independent) : a ⊥ b a\perp b a⊥b,即 p ( a , b ) = p ( a ) p ( b ) p(a,b)=p(a)p(b) p(a,b)=p(a)p(b)
-
两个随机变量条件独立(conditional independent) a ⊥ b ∣ c a\perp b|c a⊥b∣c
p ( a ∣ b , c ) = p ( a ∣ c ) p ( b ∣ a , c ) = p ( b ∣ c ) p ( a , b ∣ c ) = p ( a ∣ c ) p ( b ∣ c ) p(a|b,c)=p(a|c)\quad p(b|a,c)=p(b|c)\quad p(a,b|c)=p(a|c)p(b|c) p(a∣b,c)=p(a∣c)p(b∣a,c)=p(b∣c)p(a,b∣c)=p(a∣c)p(b∣c)
-
有向图条件独立性:D分离方法
有三种结构:



D分离法的使用:

例:

-
无向图条件独立性:条件移除方法
① 移除C中所有的节点以及连接到这些节点的边
② 判断是否存在连接A中任一节点和B中任一节点的一条路径,若不存在,则A ⊥B|C成立,否则,不成立

如果我们考虑两个结点 x i x_i xi和 x j x_j xj,它们不存在链接,那么给定图中的所有其他结点,这两个结点一定是条件独立的。这是因为两个结点之间没有直接的路径,并且所有其他的路径都通过了观测的结点,因此这些路径都是被阻隔的。这个条件独立性可以表示为:
p ( x i , x j ∣ x \ { i , j } ) = p ( x i ∣ x \ { i , j } ) p ( x j ∣ x \ { i , j } ) p\bigl(x_i,x_j\big|\textbf{x}_{\backslash\{i,j\}}\bigr)=p\bigl(x_i\big|\textbf{x}_{\backslash\{i,j\}}\bigr)p\bigl(x_j\big|\textbf{x}_{\backslash\{i,j\}}\bigr) p(xi,xj x\{i,j})=p(xi x\{i,j})p(xj x\{i,j})
5.2.4、图模型推理的概念
在一个图模型中,推理是计算某些节点的边缘分布或以一些节点为条件计算其他节点的后验概率
在很多算法中,推理可以看作是局部信息(local messages)在图中的传播(beliefpropagation)
5.3、马尔可夫随机场
5.3.1、基本概念
-
位点空间 Site Space :有限元素集合 S = { s 1 , s 2 , … , s m } S=\{s_{1},s_{2},\ldots,s_{m}\} S={s1,s2,…,sm}表示位点的集合
-
相空间 Phase Space :有限元素集合 Λ = { λ 1 , λ 2 , … , λ n } \Lambda=\{\lambda_{1},\lambda_{2},\ldots,\lambda_{n}\} Λ={λ1,λ2,…,λn}表示变量的取值空间
-
随机场:位点空间 S S S中每一个位点从相空间 Λ \Lambda Λ中取值的随机变量的集合是空间 S S S上的一个随机场 : x = { x ( s ) ∣ s ∈ S , x ( s ) ∈ Λ } \mathbf{x}=\{x(s)|s\in S,x(s)\in\Lambda\} x={x(s)∣s∈S,x(s)∈Λ}
-
一个定义在位点集合 S S S上的邻域系统(neighborhood system)定义为
N = { N s ∣ s ∈ S } N=\{N_s|s\in S\} N={Ns∣s∈S}
其中: N s = { s ′ ∈ S ∣ d ( s , s ′ ) ≤ α , s ′ ≠ s } N_s=\{s'\in S|d(s,s')\leq\alpha,s'\neq s\} Ns={s′∈S∣d(s,s′)≤α,s′=s}邻域系统的两个性质:
- 一个位点不属于自己的邻域,即 s ∉ N s s\notin N_{s} s∈/Ns
- 相邻关系是相互的,即 s ∈ N s ′ ⇔ s ′ ∈ N s s\in N_{s^{\prime}}\Leftrightarrow s^{\prime}\in N_{s} s∈Ns′⇔s′∈Ns
-
马尔科夫随机场:
对一个随机场 x = { x ( s ) ∣ s ∈ S , x ( s ) ∈ Λ } \mathbf{x}=\{x(s)|s\in S,x(s)\in\Lambda\} x={x(s)∣s∈S,x(s)∈Λ},若满足:
∀ s ∈ S , p ( x ( s ) ∣ x ( S − s ) ) = p ( x ( s ) ∣ x ( N s ) ) \forall s\in S,\quad p(x(s)|\mathbf{x}(S-s))=p(x(s)|\mathbf{x}(N_s)) ∀s∈S,p(x(s)∣x(S−s))=p(x(s)∣x(Ns))
则该随机场为关于邻域系统N的马尔可夫随机场- 含义:一个事件发生的概率只取决于相邻的事件
- 符号: p ( s ) ( x ) = d e f p ( x ( s ) ∣ x ( S − s ) ) = p ( x ( s ) ∣ x ( N s ) ) p^{(s)}(\mathbf{x})\stackrel{\mathrm{def}}{=}p(x(s)|\mathbf{x}(S-s))=p(x(s)|\mathbf{x}(N_{s})) p(s)(x)=defp(x(s)∣x(S−s))=p(x(s)∣x(Ns))称为位点s的马尔可夫局部特性

- 吉布斯分布
定义在S上的随机场
x
\mathbf x
x是一个吉布斯随机场,当且仅当
x
\mathbf x
x服从吉布斯分布:
p
(
x
)
=
1
Z
e
−
1
T
U
(
x
)
p(\mathbf{x})=\frac{1}{Z}\mathrm{e}^{-\frac{1}{T}U(\mathbf{x})}
p(x)=Z1e−T1U(x)

在马尔科夫随机场中,联合概率密度可以表示为各个变量的条件概率的乘积形式,即每个变量的概率分布仅依赖于其邻居节点的取值,所以马尔科夫随机场的概率密度就可以用一个吉布斯分布来表示

5.3.2、应用
能量函数常见的定义方式:
U
(
x
)
=
∑
s
∈
C
1
V
1
(
x
s
)
+
∑
(
s
,
s
′
)
∈
C
2
V
2
(
x
s
,
x
s
′
)
+
∑
{
s
,
s
′
,
s
′
′
}
∈
C
3
V
3
(
x
s
,
x
s
′
,
x
s
′
′
)
+
⋯
U(\mathbf{x})=\sum_{s\in C_1}V_1(\mathbf{x}_s)+\sum_{(s,s')\in C_2}V_2(\mathbf{x}_s,\mathbf{x}_{s'})+\sum_{\{s,s',s''\}\in C_3}V_3(\mathbf{x}_s,\mathbf{x}_{s'},\mathbf{x}_{s''})+\cdots
U(x)=s∈C1∑V1(xs)+(s,s′)∈C2∑V2(xs,xs′)+{s,s′,s′′}∈C3∑V3(xs,xs′,xs′′)+⋯
一般只写到三元团,后面的不再写
对于图像去噪而言:

要把有噪声的图像尽可能恢复到原始图像,其中噪声图的变量为 y i y_i yi,目标还原图变量为 x i x_i xi,两者的值域为 { − 1 , + 1 } \{-1,+1\} {−1,+1},分别代表黄色和蓝色,表示成马尔科夫随机场即为:

这个图里有两种类型的图块,每个图块有两个变量。我们用两个变量之间的关系来构建能量函数。
首先对于 x i , y i x_i,y_i xi,yi,我们认为一般情况下他俩是强相关的,即取值相同(正常噪声图像不会太离谱,不会偏差巨大),所以定义一个简单的能量函数: − η x i y i ( η > 0 ) -\eta x_i y_i(\eta>0) −ηxiyi(η>0),当两者同色时, x i y i x_iy_i xiyi为正,能量函数小,因此势函数就大,概率就大(在玻尔兹曼定义中理解)。
剩余的团块由变量 { x i , x j } \{x_i,x_j\} {xi,xj}组成,其中 i , j i,j i,j是相邻像素的下标。与之前一样,我们希望当两个像素符号相同时能量较低,当两个像素符号相反时能量较高,因此选择能量函数 − β x i x j ( β > 0 ) -\beta x_ix_j(\beta>0) −βxixj(β>0)
由于势函数是最大团块上的一个任意的非负的函数,因此我们可以将势函数与团块的子集上的任意非负函数相乘,或等价的我们可以加上对应的能量。在这个例子中,这使得我们可以为无噪声图像的每个像素 i i i加上一个额外的项 h x i hx_i hxi。这样的项具有将模型进行偏置,使得模型倾向于选择一个特定的符号,而不选择另一个符号的效果。
最终能量函数形式为:
E
(
x
,
y
)
=
h
∑
i
x
i
−
β
∑
{
i
,
j
}
x
i
x
j
−
η
∑
i
x
i
y
i
E(\mathbf{x},\mathbf{y})=h\sum_i x_i-\beta\sum_{\{i,j\}}x_ix_j-\eta\sum_i x_i y_i
E(x,y)=hi∑xi−β{i,j}∑xixj−ηi∑xiyi
之后进行优化,目的是
x
∗
=
max
p
(
x
∣
y
)
=
max
1
Z
exp
{
−
E
(
x
,
y
)
}
\mathbf{x}^*=\max p(\mathbf{x}|\mathbf{y})=\max \frac{1}{Z}\exp\{-E(\mathbf{x},\mathbf{y})\}
x∗=maxp(x∣y)=maxZ1exp{−E(x,y)}

然后选择不同的参数值,会得到不同的还原结果,
当 β = 1.0 , η = 2.1 , h = 0 \beta=1.0,\eta =2.1,h=0 β=1.0,η=2.1,h=0时还原图像为:

当 β = 0 \beta =0 β=0时,还原出来效果是噪声图本身,没作用,因为能量函数中只剩下 η x i y i \eta x_iy_i ηxiyi会使得 x i = y i x_i=y_i xi=yi。
参考自:【PRML】【模式识别和机器学习】【从零开始的公式推导】8.3马尔可夫随机场
5.4、隐马尔可夫模型
5.4.1、引例
一个人随机挑选盒子摸一个球,然后和另一个人说颜色,从观测者的角度来看问题。

用图模型表示出来,分为:
- 过程1: 可观测过程,从被选到的盒子中随机抽取彩色球并观察其颜色
- 过程2: 隐藏过程, 随机选择抽取彩色球的盒子
正式定义:
隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列、再由各个状态生成一个观测 由此产生可观测随机序列的过程。
隐藏的马尔可夫链随机生成的状态的序列称为状态序列(state sequence),每个状态生成一个观测,而由此产生的观测的随机序列称为观测序列(observation sequence),序列的每一个位置可以看作是一个时刻。
5.4.2、组成要素
(1) 状态空间
S
:
H
M
M
S: \mathrm{HMM}
S:HMM 的状态空间通常是可数的,元素可表示为
i
,
j
,
k
,
…
i, j, k, \ldots
i,j,k,… 。尽管
H
M
M
\mathrm{HMM}
HMM 的状态是隐藏的,但在实际应用中都有明确的物理意义。比如,用HMM 模拟上述彩色球抽取实验,每个状态将对应一个包含
M
M
M 种颜色球的盒子,共N个盒子。
(2) 输出集/观测集
Y
:
Y:
Y: 元素
y
i
∈
Y
y_i \in Y
yi∈Y 对应系统的一个物理输出。在彩色球抽取实验中, 输出对应抽取到的球的颜色
(3) 状态转移矩阵:
P
=
{
p
i
j
}
,
p
i
j
=
P
(
j
∣
i
)
(
i
,
j
∈
S
)
\boldsymbol{P}=\left\{p_{i j}\right\} , p_{i j}=P(j \mid i)(i, j \in S)
P={pij},pij=P(j∣i)(i,j∈S) 表示从状态
i
i
i转移到
j
j
j 的概率
(4) 输出概率/观测概率分布矩阵:
Q
=
{
q
s
y
}
,
q
s
y
=
P
(
y
∣
s
)
\boldsymbol{Q}=\left\{q_{s y}\right\} , q_{s y}=P(y \mid s)
Q={qsy},qsy=P(y∣s) 是状态
s
s
s 下输出
y
y
y 的概率,
y
∈
Y
,
s
∈
S
y \in Y, \quad s \in S
y∈Y,s∈S
(5) 初始状态分布:
π
=
{
π
i
}
,
i
∈
S
,
π
i
\pi=\left\{\pi_i\right\} , i \in S , \pi_i
π={πi},i∈S,πi 表示初始状态为
i
i
i 的概率
p
(
s
,
y
)
=
p
(
s
1
,
s
2
,
…
,
s
n
,
y
1
,
y
2
,
…
,
y
n
)
=
p
(
s
1
)
∏
i
=
1
n
p
(
y
i
∣
s
i
)
∏
i
=
2
n
p
(
s
i
∣
s
i
−
1
)
=
π
s
1
q
s
1
y
1
∏
i
=
2
n
p
s
i
−
1
s
i
q
s
i
y
i
\begin{array}{l}p(s,y)=p\big(s_1,s_2,\ldots,s_n,y_1,y_2,\ldots,y_n\big)\\ =p(s_1)\prod_{i=1}^{n}p(y_i|s_i)\prod_{i=2}^{n}p(s_i|s_{i-1})=\pi_{s_1}q_{s_1y_1}\prod_{i=2}^{n}p_{s_{i-1}s_i}q_{s_iy_i}\end{array}
p(s,y)=p(s1,s2,…,sn,y1,y2,…,yn)=p(s1)∏i=1np(yi∣si)∏i=2np(si∣si−1)=πs1qs1y1∏i=2npsi−1siqsiyi

总的来说, S 和 Y S和Y S和Y对应 HMM 的模型结构 ,而 λ = ( P , Q , π ) \boldsymbol{\lambda}=(P,\boldsymbol{Q},\boldsymbol{\pi}) λ=(P,Q,π)对应HMM的参数
HMM的全部参数可以表示成一个矩阵的形式:
-
π \pi π叫做初始概率矩阵,是一个N维向量 π i = p ( s 1 = s i ) \pi_i=p(s_1=s_i) πi=p(s1=si)
-
P叫做转移概率矩阵,是一个N×N维矩阵, A i j = P ( s j ∣ s i ) A_{i j}=P(s_{j}|s_{i}) Aij=P(sj∣si)
-
Q叫做观测概率矩阵,是一个N×M维矩阵, A i j = P ( y j ∣ s i ) A_{i j}=P(y_{j}|s_{i}) Aij=P(yj∣si)
假如说有4个盒子,黑白两种颜色,即N=4,M=2
则初始概率分布为:
π
=
(
0.25
,
0.25
,
0.25
,
0.25
)
T
\pi=\left(0.25,0.25,0.25,0.25\right)^{\mathrm{T}}
π=(0.25,0.25,0.25,0.25)T
状态转移概率分布为:
P
=
[
0
1
0
0
0.4
0
0.6
0
0
0.4
0
0.6
0
0
0.5
0.5
]
P=\left[\begin{array}{cccc}0&1&0&0\\ 0.4&0&0.6&0\\ 0&0.4&0&0.6\\ 0&0&0.5&0.5\end{array}\right]
P=
00.400100.4000.600.5000.60.5
观测概率分布为:
Q
=
[
0.5
0.5
0.3
0.7
0.6
0.4
0.8
0.2
]
Q=\left[\begin{array}{ccc}0.5&0.5\\ 0.3&0.7\\ 0.6&0.4\\ 0.8&0.2\end{array}\right]
Q=
0.50.30.60.80.50.70.40.2
5.4.3、基本问题
-
问题1:给定模型参数 λ \lambda λ和观测序列 y = ( y 1 , y 2 , … y n ) \mathbf y=(y_1,y_2,\dots y_n) y=(y1,y2,…yn) 计算此观测序列出现的概率 p ( y ∣ λ ) p(\mathbf y|\lambda) p(y∣λ)。(能否计算出观测到某一特定颜色序列的概率?)
-
直接解决方法:把 p ( y 1 , y 2 , … , y n ) p(y_{1},y_{2},\ldots,y_{n}) p(y1,y2,…,yn)看做边缘概率密度,在所有可能的状态转移序列 s 1 , s 2 , … s n s_1,s_2,\dots s_n s1,s2,…sn上求和
p ( y 1 , y 2 , … , y n ) = ∑ s 1 , … , s n p ( s 1 , s 2 , … , s n , y 1 , y 2 , … , y n ) = ∑ s 1 ∑ s 2 … ∑ s n p ( s 1 , s 2 , … , s n , y 1 , y 2 , … , y n ) = ∑ s 1 ∑ s 2 … ∑ s n p ( s 1 ) ∏ i = 1 n p ( y i ∣ s i ) ∏ i = 2 n p ( s i ∣ s i − 1 ) \begin{array}{c}{{p(y_{1},y_{2},\ldots,y_{n})=\sum_{s_{1},\ldots,s_{n}}p(s_{1},s_{2},\ldots,s_{n},y_{1},y_{2},\ldots,y_{n})}}\\ {{=\sum_{s_{1}}\sum_{s_{2}}\ldots\sum_{s_{n}}p(s_{1},s_{2},\ldots,s_{n},y_{1},y_{2},\ldots,y_{n})}}\\ {{=\sum_{s_{1}}\sum_{s_{2}}\ldots\sum_{s_{n}}p(s_{1})\prod_{i=1}^{n}p(y_{i}|s_{i})\prod_{i=2}^{n}p(s_{i}|s_{i-1})}}\end{array} p(y1,y2,…,yn)=∑s1,…,snp(s1,s2,…,sn,y1,y2,…,yn)=∑s1∑s2…∑snp(s1,s2,…,sn,y1,y2,…,yn)=∑s1∑s2…∑snp(s1)∏i=1np(yi∣si)∏i=2np(si∣si−1)
这种方法时间复杂度为: O ( 2 n ∣ S ∣ n ) O(2n|S|^{n}) O(2n∣S∣n)难操作,(|S|为状态空间S的状态数) -
前向算法:利用递归关系
推导如下:
p ( y 1 , y 2 , … y n ) = ∑ i = 1 ∣ S ∣ p ( y 1 , y 2 , … , y n , s n = i ) p(y_{1},y_{2},\ldots y_{n})=\sum_{i=1}^{|S|}p(y_{1},y_{2},\ldots,y_{n},s_{n}=i) p(y1,y2,…yn)=i=1∑∣S∣p(y1,y2,…,yn,sn=i)
其中: p ( y 1 , y 2 , … , y t , s t ) = p ( y 1 , y 2 , … , y t ∣ s t ) p ( s t ) p(y_1,y_2,\ldots,y_t,s_t)=p(y_1,y_2,\ldots,y_t|s_t)p(s_t) p(y1,y2,…,yt,st)=p(y1,y2,…,yt∣st)p(st),此时 s t s_t st是个变量
= p ( y t ∣ s t ) p ( y 1 , y 2 , … , y t − 1 ∣ s t ) p ( s t ) = p ( y t ∣ s t ) p ( y 1 , y 2 , … , y t − 1 , s t ) = p ( y t ∣ s t ) ∑ s t − 1 p ( y 1 , y 2 , … , y t − 1 , s t − 1 , s t ) = p ( y t ∣ s t ) ∑ s t − 1 p ( y 1 , y 2 , … , y t − 1 , s t ∣ s t − 1 ) p ( s t − 1 ) = p ( y t ∣ s t ) ∑ s t − 1 p ( y 1 , y 2 , … , y t − 1 ∣ s t − 1 ) p ( s t ∣ s t − 1 ) p ( s t − 1 ) = p ( y t ∣ s t ) ∑ s t − 1 p ( y 1 , y 2 , … , y t − 1 , s t − 1 ) p ( s t ∣ s t − 1 ) \begin{array}{l}=p(y_t|s_t)p(y_1,y_2,\ldots,y_{t-1}|s_t)p(s_t)=p(y_t|s_t)p(y_1,y_2,\ldots,y_{t-1},s_t)\\ =p(y_t|s_t)\sum_{s_{t-1}}p(y_1,y_2,\ldots,y_{t-1},s_{t-1},s_{t})\\ \begin{array}{l}=p(y_t|s_t)\sum_{s_{t-1}}p(y_1,y_2,\ldots,y_{t-1},s_t|s_{t-1})p(s_{t-1})\\ =p(y_t|s_t)\sum_{s_{t-1}}p(y_1,y_2,\ldots,y_{t-1}|s_{t-1})p(s_t|s_{t-1})p(s_{t-1})\\ =p(y_t|s_t)\sum_{s_{t-1}}p(y_1,y_2,\ldots,y_{t-1},s_{t-1})p(s_t|s_{t-1})\\ \end{array} \end{array} =p(yt∣st)p(y1,y2,…,yt−1∣st)p(st)=p(yt∣st)p(y1,y2,…,yt−1,st)=p(yt∣st)∑st−1p(y1,y2,…,yt−1,st−1,st)=p(yt∣st)∑st−1p(y1,y2,…,yt−1,st∣st−1)p(st−1)=p(yt∣st)∑st−1p(y1,y2,…,yt−1∣st−1)p(st∣st−1)p(st−1)=p(yt∣st)∑st−1p(y1,y2,…,yt−1,st−1)p(st∣st−1)
用更简洁的形式来表示:
a t = p ( y 1 , y 2 , … , y t , s t ) a t = p ( y t ∣ s t ) ∑ s t − 1 a t − 1 p ( s t ∣ s t − 1 ) \begin{array}{l}{a_{t}=p(y_{1},y_{2},\ldots,y_{t},s_{t})}\\ {a_{t}=p(y_{t}|s_{t})\sum_{s_{t-1}}a_{t-1}p(s_{t}|s_{t-1})}\\ \end{array} at=p(y1,y2,…,yt,st)at=p(yt∣st)∑st−1at−1p(st∣st−1)
总流程如下:-
初始化: a 1 ( i ) = π i q i y 1 1 ≤ i ≤ ∣ S ∣ a_{1}(i)=\pi_{i}q_{i y_{1}}1\leq i\leq|S| a1(i)=πiqiy11≤i≤∣S∣得出S个结果
-
递归: a t ( j ) = [ ∑ i = 1 ∣ S ∣ α t − 1 ( i ) p i j ] q j y t 2 ≤ t ≤ n , 1 ≤ j ≤ ∣ S ∣ a_t(j)=\left[\sum_{i=1}^{|S|}\alpha_{t-1}(i)p_{ij}\right]q_{jy_t}\,2\leq t\leq n,1\leq j\leq|S| at(j)=[∑i=1∣S∣αt−1(i)pij]qjyt2≤t≤n,1≤j≤∣S∣,
对于n个状态的S个状态选择及已知观测值得出结果

-
p ( y 1 , y 2 , … , y n ∣ λ ) = ∑ i = 1 ∣ S ∣ a n ( i ) p(y_1,y_2,\ldots,y_n|\lambda)=\sum_{i=1}^{|S|}a_n(i) p(y1,y2,…,yn∣λ)=∑i=1∣S∣an(i)
最后一个状态空间累和得出结果
最终的时间复杂度为每个状态的 ∣ S ∣ 2 |S|^2 ∣S∣2的计算乘以状态数 n n n,即 O ( n ∣ S ∣ 2 ) O(n|S|^2) O(n∣S∣2),比直接求解大大降低
-
最后看一个李航书上的例子:



-
-
问题二:给定模型参数 λ \lambda λ和观测序列 y = ( y 1 , y 2 , … y n ) \mathbf y=(y_1,y_2,\dots y_n) y=(y1,y2,…yn),如何才能计算出最可能生成观测序列 y \mathbf y y的状态序列 s ∗ = ( s 1 , s 2 , . . . s n ) \boldsymbol{s}^{*}=(s_{1},s_{2},...s_{n}) s∗=(s1,s2,...sn)(给定特定的颜色观测序列,能否计算出最有可能的球被抽取出的盒子序列?)
p ( s 1 , s 2 , … , s n ∣ y 1 , y 2 , … , y n ) = p ( s 1 , s 2 , … , s n y 1 , y 2 , … , y n ) p ( y 1 , y 2 , … , y n ) ⇔ arg max p ( s ∣ y , λ ) = arg max p ( s 1 , s 2 , … , s n , y 1 , y 2 , … , y n ) p(s_1,s_2,\ldots,s_n|y_1,y_2,\ldots,y_n)=\frac{p(s_1,s_2,\ldots,s_n y_1,y_2,\ldots,y_n)}{p(y_1,y_2,\ldots,y_n)}\\ \Leftrightarrow \ \arg\max p(\mathbf{s}|\mathbf{y},\lambda)=\arg \max p(s_1,s_2,\ldots,s_n,y_1,y_2,\ldots,y_n)\\ p(s1,s2,…,sn∣y1,y2,…,yn)=p(y1,y2,…,yn)p(s1,s2,…,sny1,y2,…,yn)⇔ argmaxp(s∣y,λ)=argmaxp(s1,s2,…,sn,y1,y2,…,yn)
通过条件独立性又有:
p ( s 1 , … , s t , s t + 1 , … , s n , y 1 , … , y t , y t + 1 , … , y n ) = p ( s 1 , … , s t , y 1 , … , y t ) p ( s t + 1 , … , s n , y t + 1 , … , y n ∣ s 1 , … , s t , y 1 , … , y t ) = p ( s 1 , … , s t , y 1 , … , y t ) p ( s t + 1 , … , s n , y t + 1 , … , y n ∣ s t ) p(s_{1},\ldots,s_{t},s_{t+1},\ldots,s_{n},y_{1},\ldots,y_{t},y_{t+1},\ldots,y_{n})\\ =p(s_{1},\ldots,s_{t},y_{1},\ldots,y_{t})p(s_{t+1},\ldots,s_{n},y_{t+1},\ldots,y_{n}|s_{1},\ldots,s_{t},y_{1},\ldots,y_{t})\\ =p(s_1,\ldots,s_t,y_1,\ldots,y_t)p(s_{t+1},\ldots,s_n,y_{t+1},\ldots,y_n|s_t) p(s1,…,st,st+1,…,sn,y1,…,yt,yt+1,…,yn)=p(s1,…,st,y1,…,yt)p(st+1,…,sn,yt+1,…,yn∣s1,…,st,y1,…,yt)=p(s1,…,st,y1,…,yt)p(st+1,…,sn,yt+1,…,yn∣st)
因此:
max s 1 , s 2 , … , s n p ( s 1 , … , s t , s t + 1 , … , s n , y 1 , … , y t , y t + 1 , … , y n ) = max s 1 , s t + 1 , … , s n [ p ( s t + 1 , … , s n , y t + 1 , … , y n ∣ s t ) × max s 1 , s 2 , … , s t − 1 p ( s 1 , … , s t − 1 s t , y 1 … , … , y t ) ] \max\limits_{s_1,s_2,\ldots,s_n}p(s_1,\ldots,s_t,s_{t+1},\ldots,s_n,y_1,\ldots,y_t,y_{t+1},\ldots,y_n)\\ =\max\limits_{s_1,s_{t+1},\ldots,s_n}[p(s_{t+1},\ldots,s_n,y_{t+1},\ldots,y_n|s_t)\times\max\limits_{s_1,s_2,\ldots,s_{t-1}}p(s_1,\ldots,s_{t-1}s_{t},y_1\ldots,\ldots,y_t)] s1,s2,…,snmaxp(s1,…,st,st+1,…,sn,y1,…,yt,yt+1,…,yn)=s1,st+1,…,snmax[p(st+1,…,sn,yt+1,…,yn∣st)×s1,s2,…,st−1maxp(s1,…,st−1st,y1…,…,yt)]注意上式右侧是通过找到 s 1 , s 2 , … , s t − 1 s_1,s_2,\ldots,s_{t-1} s1,s2,…,st−1来使概率最大,此时 s t s_t st仍是变量形式
定义: γ t ( i ) = max s 1 , s 2 , … , s t − 1 p ( s 1 , … , s t − 1 , s t = i , y 1 , … , y t ) \gamma_t\left(i\right)=\max\limits_{s_1,s_2,\ldots,s_{t-1}}p(s_1,\ldots,s_{t-1},s_t=i,y_1,\ldots,y_t) γt(i)=s1,s2,…,st−1maxp(s1,…,st−1,st=i,y1,…,yt)
得到:
max s 1 , s 2 , … , s n p ( s 1 , … , s t , s t + 1 , … , s n , y 1 , … , y t , y t + 1 , … , y n ) = max i { max s t + 1 , … , s n [ p ( s t + 1 , … , s n , y t + 1 , … , y n ∣ s t = i ) γ t ( i ) } \begin{array}{c}\max\limits_{s_1,s_2,\ldots,s_n}p(s_1,\ldots,s_t,s_{t+1},\ldots,s_n,y_1,\ldots,y_{t},y_{t+1},\ldots,y_n)\\ \\ =\max\limits_{i} \left \{ \max \limits_{s_{t+1},\ldots,s_n}[p(s_{t+1},\ldots,s_n,y_{t+1},\ldots,y_n|s_t=i)\gamma_t\left(i\right)\right\}\end{array} s1,s2,…,snmaxp(s1,…,st,st+1,…,sn,y1,…,yt,yt+1,…,yn)=imax{st+1,…,snmax[p(st+1,…,sn,yt+1,…,yn∣st=i)γt(i)}

一言以蔽之:对于t时刻状态的每一个取值,找到前面到达它的最优路径和后面他到达终点的最优路径,然后在t时刻的这些状态里取最大,动态规划思想。
在计算 γ t ( i ) \gamma_t(i) γt(i)时可以使用递归:
γ t + 1 ( j ) = ( max i γ t ( i ) p ( s t + 1 = j ∣ s t = i ) ) p ( y t + 1 ∣ s t + 1 = j ) \gamma_{t+1}\left(j\right)=\left(\max\limits_{i}\gamma_{t}\left(i\right)p(s_{t+1}=j|s_{t}=i)\right)p(y_{t+1}|s_{t+1}=j) γt+1(j)=(imaxγt(i)p(st+1=j∣st=i))p(yt+1∣st+1=j)
归结为维特比算法来计算:
最后再看一个李航书上的例子:






- 问题3:给定多个观测序列
y
i
\mathbf y_i
yi,我们如何才能找出最优模型参数集
λ
\lambda
λ,使得对所有的
y
i
\mathbf y_i
yi,
p
(
y
∣
λ
)
p(\mathbf y|\lambda)
p(y∣λ)最大(给定多个观测序列,能否计算出两个盒子之间的转移概率,以及从每一个盒子中观测到特定颜色的概率?)
…………
参考
《统计学习方法(第二版)》
《Pattern Recognition and Machine Learning》
老师上课的PPT