近几天看到论文里面有T分布随机近邻嵌入（T-distributed stochastic neighbor embedding, T-SNE）这种可视化方法，以前好像也看到过，但没有系统了解过，现有时间正好实践记录一下。

1. T-SNE简介

  T-SNE是一种降维方法，降维？PCA（Principal component analysis）也可以降维，T-SNE有什么特点呢？T-SNE是非线性的，而PCA是线性的。T-SNE非线性降维的思路是将高维特征投射到低维空间，使得原本在高维空间距离较远的数据点在低维空间同样距离较远，而原本在高维空间距离较近的数据点在低维空间同样距离较近。低维空间一般设为2维或者3维，方便可视化。

  然而，T-SNE很少用于降维，论文中看到的基本是用来可视化的，因为一般需要降维的数据都具有线性相关性，故PCA用的比较多。T-SNE可视化原始数据的分布，度量原始数据信息的相关性；T-SNE可视化神经网络提取的特征，评估不同模型的优劣性。本质上，近邻嵌入寻找保留了样本邻居关系在新维度上的较低数据表示。

  T-SNE理论详解

2. T-SNE的Python实践

  Python中实现T-SNE采用sklearn.manifold模块中的TSNE类。
TSNE类有几个重要参数：
  （1）n_components：嵌入空间的尺寸，即降维维度，其默认值为2。
  （2）perplexity：困惑度，与流形学习算法中使用的最近邻的数量有关，通常情况下，大数据集需要大困惑度，考虑选择5到50之间的值，不同的值可能导致显著不同的结果，perplexity的默认值为30。
  （3）learning_rate：T-SNE的学习率通常在[10.0,1000.0]范围内。如果学习率太高，数据可能看起来像一个“球”，任何一点与它最近的邻居的距离都差不多；如果学习率太低，大多数点可能看起来被压缩在密集的云中，几乎没有离群值；如果代价函数陷入一个糟糕的局部最小值，增加学习率可能会有所帮助，learning_rate的默认值为200。
  （4）n_iter：优化的最大迭代次数，至少应该是250，其默认值为1000。

用鸢尾花数据来试试T-SNE：设置降维到2

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.manifold import TSNE
from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

tsne = TSNE(n_components=2, perplexity=15).fit_transform(X)
aa = tsne[:, 0]
bb = tsne[:, 1]

color = ['limegreen', 'cornflowerblue', 'orange']

plt.figure(dpi=300)
for i in range(tsne.shape[0]):
    plt.scatter(aa[i], bb[i], facecolor=color[y[i]], alpha=0.7)
plt.savefig('./tsne_2.jpg')
plt.show()

输出为：

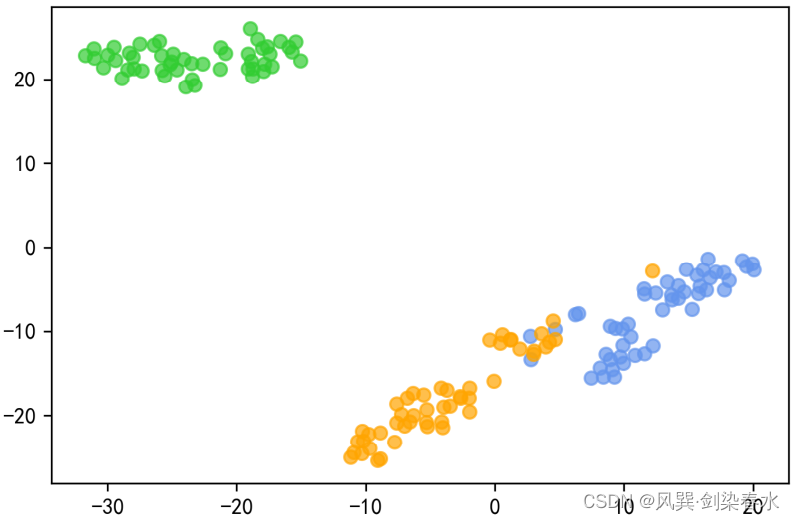
值得注意的是：T-SNE每次运行会得到不同的可视化图像，但不同类别之间的距离是相似的

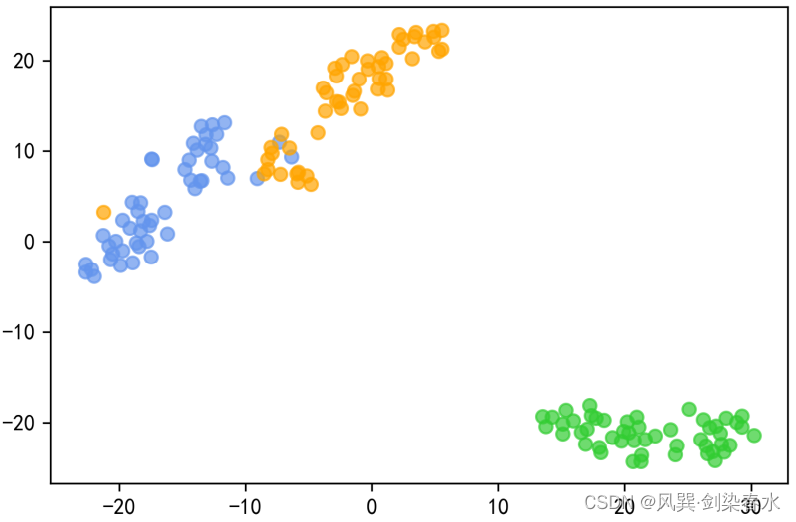
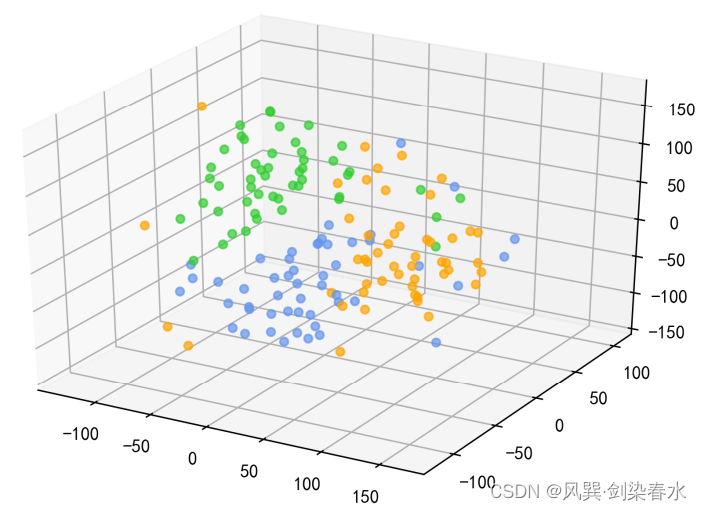
同样的，降低到3维也可以进行可视化

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.manifold import TSNE
from sklearn.datasets import load_iris

iris = load_iris()
X = iris.data
y = iris.target

tsne = TSNE(n_components=3, perplexity=15).fit_transform(X)
aa = tsne[:, 0]
bb = tsne[:, 1]
cc = tsne[:, 2]

color = ['limegreen', 'cornflowerblue', 'orange']

fig = plt.figure(dpi=300)
ax = Axes3D(fig)
for i in range(tsne.shape[0]):
    ax.scatter(aa[i], bb[i], cc[i], facecolor=color[y[i]], alpha=0.7)
plt.show()