【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

专栏详细介绍：【深度学习入门到进阶】必看系列，含激活函数、优化策略、损失函数、模型调优、归一化算法、卷积模型、序列模型、预训练模型、对抗神经网络等

本专栏主要方便入门同学快速掌握相关知识。声明：部分项目为网络经典项目方便大家快速学习，后续会不断增添实战环节（比赛、论文、现实应用等）

专栏订阅：深度学习入门到进阶专栏

深度学习基础入门篇[9.2]：卷积之1*1 卷积、2D/3D卷积、转置卷积

1.1*1 卷积

$1\times 1$ 卷积，与标准卷积完全一样，唯一的特殊点在于卷积核的尺寸是$1\times 1$ ，也就是不去考虑输入数据局部信息之间的关系，而把关注点放在不同通道间。当输入矩阵的尺寸为$3\times 3$ ，通道数也为3时，使用4个$1\times 1$卷积核进行卷积计算，最终就会得到与输入矩阵尺寸相同，通道数为4的输出矩阵，如 图1 所示。

图1 1*1 卷积结构示意图

• $1\times 1$ 卷积的作用

1. 实现信息的跨通道交互与整合。考虑到卷积运算的输入输出都是3个维度（宽、高、多通道），所以$1\times 1$ 卷积实际上就是对每个像素点，在不同的通道上进行线性组合，从而整合不同通道的信息。

2. 对卷积核通道数进行降维和升维，减少参数量。经过$1\times 1$ 卷积后的输出保留了输入数据的原有平面结构，通过调控通道数，从而完成升维或降维的作用。

3. 利用$1\times 1$ 卷积后的非线性激活函数，在保持特征图尺寸不变的前提下，大幅增加非线性

1.1 1*1 卷积在GoogLeNet中的应用

• $1\times 1$ 卷积在GoogLeNet[1]中的应用

GoogLeNet是2014年ImageNet比赛的冠军，它的主要特点是网络不仅有深度，还在横向上具有“宽度”。由于图像信息在空间尺寸上的巨大差异，如何选择合适的卷积核来提取特征就显得比较困难了。空间分布范围更广的图像信息适合用较大的卷积核来提取其特征；而空间分布范围较小的图像信息则适合用较小的卷积核来提取其特征。为了解决这个问题，GoogLeNet提出了一种被称为Inception模块的方案。如 图2 所示：

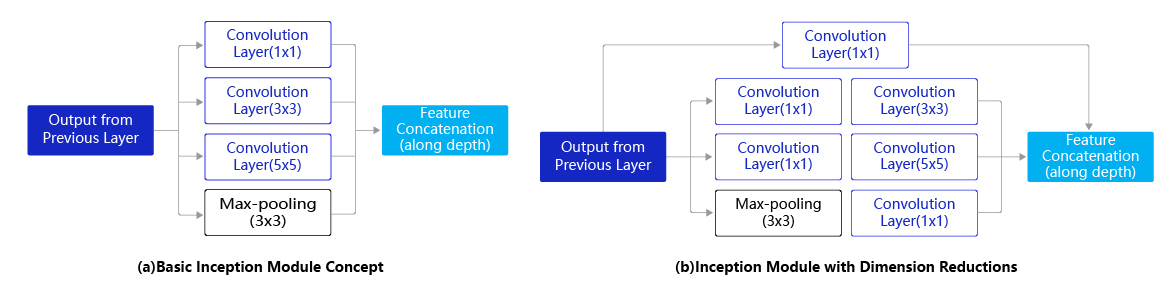
图2 Inception模块结构示意图

Inception模块的设计思想采用多通路(multi-path)的设计形式，每个支路使用不同大小的卷积核，最终输出特征图的通道数是每个支路输出通道数的总和。如 图2(a) 所示，Inception模块使用3个不同大小的卷积核对输入图片进行卷积操作，并附加最大池化，将这4个操作的输出沿着通道维度进行拼接，构成的输出特征图将会包含经过不同大小的卷积核提取出来的特征，从而达到捕捉不同尺度信息的效果。然而，这将会导致输出通道数变得很大，尤其是将多个Inception模块串联操作的时候，模型参数量会变得非常大。

为了减小参数量，Inception模块改进了设计方式。如 图2(b) 所示，在$3\times 3$ 和$5\times 5$ 的卷积层之前均增加$1\times 1$ 的卷积层来控制输出通道数；在最大池化层后面增加$1\times 1$ 卷积层减小输出通道数。下面这段程序是Inception块的具体实现方式，可以对照 图2(b) 和代码一起阅读。

我们这里可以简单计算一下Inception模块中使用$1\times 1$ 卷积前后参数量的变化，这里以 图2(a) 为例，输入通道数 $C_{in}=192$，$1\times 1$ 卷积的输出通道数$C_{out1}=64$，$3\times 3$ 卷积的输出通道数$C_{out2}=128$，$5\times 5$ 卷积的输出通道数$C_{out3}=32$，则 图2(a) 中的结构所需的参数量为：

$$1\times 1\times 192\times 64+3\times 3\times 192\times 128+5\times 5\times 192\times 32=387072$$

图2(b) 中在$3\times 3$ 卷积前增加了通道数$C_{out4}=96$ 的 $1\times 1$ 卷积，在$5\times 5$ 卷积前增加了通道数$C_{out5}=16$ 的 $1\times 1$ 卷积，同时在maxpooling后增加了通道数$C_{out6}=32$ 的 $1\times 1$ 卷积，参数量变为：

KaTeX parse error: No such environment: eqnarray at position 21: …n{split} \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲\small{ 1\times…

可见，$1\times 1$ 卷积可以在不改变模型表达能力的前提下，大大减少所使用的参数量。

Inception模块的具体实现如下代码所示：

# GoogLeNet模型代码
import numpy as np
import paddle
from paddle.nn import Conv2D, MaxPool2D, AdaptiveAvgPool2D, Linear
## 组网
import paddle.nn.functional as F

# 定义Inception块
class Inception(paddle.nn.Layer):
    def __init__(self, c0, c1, c2, c3, c4, **kwargs):
        '''
        Inception模块的实现代码，
        
        c1,图(b)中第一条支路1x1卷积的输出通道数，数据类型是整数
        c2,图(b)中第二条支路卷积的输出通道数，数据类型是tuple或list, 
               其中c2[0]是1x1卷积的输出通道数，c2[1]是3x3
        c3,图(b)中第三条支路卷积的输出通道数，数据类型是tuple或list, 
               其中c3[0]是1x1卷积的输出通道数，c3[1]是3x3
        c4,图(b)中第一条支路1x1卷积的输出通道数，数据类型是整数
        '''
        super(Inception, self).__init__()
        # 依次创建Inception块每条支路上使用到的操作
        self.p1_1 = Conv2D(in_channels=c0,out_channels=c1, kernel_size=1)
        self.p2_1 = Conv2D(in_channels=c0,out_channels=c2[0], kernel_size=1)
        self.p2_2 = Conv2D(in_channels=c2[0],out_channels=c2[1], kernel_size=3, padding=1)
        self.p3_1 = Conv2D(in_channels=c0,out_channels=c3[0], kernel_size=1)
        self.p3_2 = Conv2D(in_channels=c3[0],out_channels=c3[1], kernel_size=5, padding=2)
        self.p4_1 = MaxPool2D(kernel_size=3, stride=1, padding=1)
        self.p4_2 = Conv2D(in_channels=c0,out_channels=c4, kernel_size=1)

    def forward(self, x):
        # 支路1只包含一个1x1卷积
        p1 = F.relu(self.p1_1(x))
        # 支路2包含 1x1卷积 + 3x3卷积
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        # 支路3包含 1x1卷积 + 5x5卷积
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        # 支路4包含 最大池化和1x1卷积
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 将每个支路的输出特征图拼接在一起作为最终的输出结果
        return paddle.concat([p1, p2, p3, p4], axis=1)

1.2 1*1 卷积在ResNet中的应用–残差网络

随着深度学习的不断发展，模型的层数越来越多，网络结构也越来越复杂。但是增加网络的层数之后，训练误差往往不降反升。由此，Kaiming He等人提出了残差网络ResNet来解决上述问题。ResNet是2015年ImageNet比赛的冠军，将识别错误率降低到了3.6%，这个结果甚至超出了正常人眼识别的精度。在ResNet中，提出了一个非常经典的结构—残差块（Residual block）。

残差块是ResNet的基础，具体设计方案如 图3 所示。不同规模的残差网络中使用的残差块也并不相同，对于小规模的网络，残差块如 图3(a) 所示。但是对于稍大的模型，使用 图3(a) 的结构会导致参数量非常大，因此从ResNet50以后，都是使用 图3(b) 的结构。图3(b) 中的这种设计方案也常称作瓶颈结构（BottleNeck）。11的卷积核可以非常方便的调整中间层的通道数，在进入33的卷积层之前减少通道数（256->64），经过该卷积层后再恢复通道数(64->256)，可以显著减少网络的参数量。这个结构（256->64->256）像一个中间细，两头粗的瓶颈，所以被称为“BottleNeck”。

我们这里可以简单计算一下残差块中使用$1\times 1$ 卷积前后参数量的变化，为了保持统一，我们令图3中的两个结构的输入输出通道数均为256，则图3(a)中的结构所需的参数量为：

$$3\times 3\times 256\times 256\times 2=1179648$$

而图3(b)中采用了$1\times 1$ 卷积后，参数量为：

$$1\times 1\times 256\times 64+3\times 3\times 64\times 64+1\times 1\times 64\times 256=69632$$

同样，$1\times 1$ 卷积可以在不改变模型表达能力的前提下，大大减少所使用的参数量。

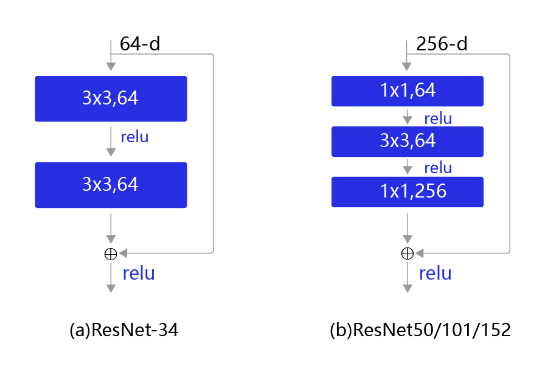
图3 残差块结构示意图

残差块的具体实现如下代码所示：

# ResNet模型代码
import numpy as np
import paddle
import paddle.nn as nn
import paddle.nn.functional as F

# ResNet中使用了BatchNorm层，在卷积层的后面加上BatchNorm以提升数值稳定性
# 定义卷积批归一化块
class ConvBNLayer(paddle.nn.Layer):
    def __init__(self,
                 num_channels,
                 num_filters,
                 filter_size,
                 stride=1,
                 groups=1,
                 act=None):
       
        """
        num_channels, 卷积层的输入通道数
        num_filters, 卷积层的输出通道数
        stride, 卷积层的步幅
        groups, 分组卷积的组数，默认groups=1不使用分组卷积
        """
        super(ConvBNLayer, self).__init__()

        # 创建卷积层
        self._conv = nn.Conv2D(
            in_channels=num_channels,
            out_channels=num_filters,
            kernel_size=filter_size,
            stride=stride,
            padding=(filter_size - 1) // 2,
            groups=groups,
            bias_attr=False)

        # 创建BatchNorm层
        self._batch_norm = paddle.nn.BatchNorm2D(num_filters)
        
        self.act = act

    def forward(self, inputs):
        y = self._conv(inputs)
        y = self._batch_norm(y)
        if self.act == 'leaky':
            y = F.leaky_relu(x=y, negative_slope=0.1)
        elif self.act == 'relu':
            y = F.relu(x=y)
        return y

# 定义残差块
# 每个残差块会对输入图片做三次卷积，然后跟输入图片进行短接
# 如果残差块中第三次卷积输出特征图的形状与输入不一致，则对输入图片做1x1卷积，将其输出形状调整成一致
class BottleneckBlock(paddle.nn.Layer):
    def __init__(self,
                 num_channels,
                 num_filters,
                 stride,
                 shortcut=True):
        super(BottleneckBlock, self).__init__()
        # 创建第一个卷积层 1x1
        self.conv0 = ConvBNLayer(
            num_channels=num_channels,
            num_filters=num_filters,
            filter_size=1,
            act='relu')
        # 创建第二个卷积层 3x3
        self.conv1 = ConvBNLayer(
            num_channels=num_filters,
            num_filters=num_filters,
            filter_size=3,
            stride=stride,
            act='relu')
        # 创建第三个卷积 1x1，但输出通道数乘以4
        self.conv2 = ConvBNLayer(
            num_channels=num_filters,
            num_filters=num_filters * 4,
            filter_size=1,
            act=None)

        # 如果conv2的输出跟此残差块的输入数据形状一致，则shortcut=True
        # 否则shortcut = False，添加1个1x1的卷积作用在输入数据上，使其形状变成跟conv2一致
        if not shortcut:
            self.short = ConvBNLayer(
                num_channels=num_channels,
                num_filters=num_filters * 4,
                filter_size=1,
                stride=stride)

        self.shortcut = shortcut

        self._num_channels_out = num_filters * 4

    def forward(self, inputs):
        y = self.conv0(inputs)
        conv1 = self.conv1(y)
        conv2 = self.conv2(conv1)

        # 如果shortcut=True，直接将inputs跟conv2的输出相加
        # 否则需要对inputs进行一次卷积，将形状调整成跟conv2输出一致
        if self.shortcut:
            short = inputs
        else:
            short = self.short(inputs)

        y = paddle.add(x=short, y=conv2)
        y = F.relu(y)
        return y

参考文献

[1] Going deeper with convolutions

[2] Deep Residual Learning for Image Recognition

2. 3D卷积（3D Convolution）

2.1 3D卷积

标准卷积是一种2D卷积，计算方式如 图1 所示。在2D卷积中，卷积核在图片上沿着宽和高两个维度滑动，在每次滑动过程时，对应位置的图像元素与卷积核中的参数进行乘加计算，得到输出特征图中的一个值。

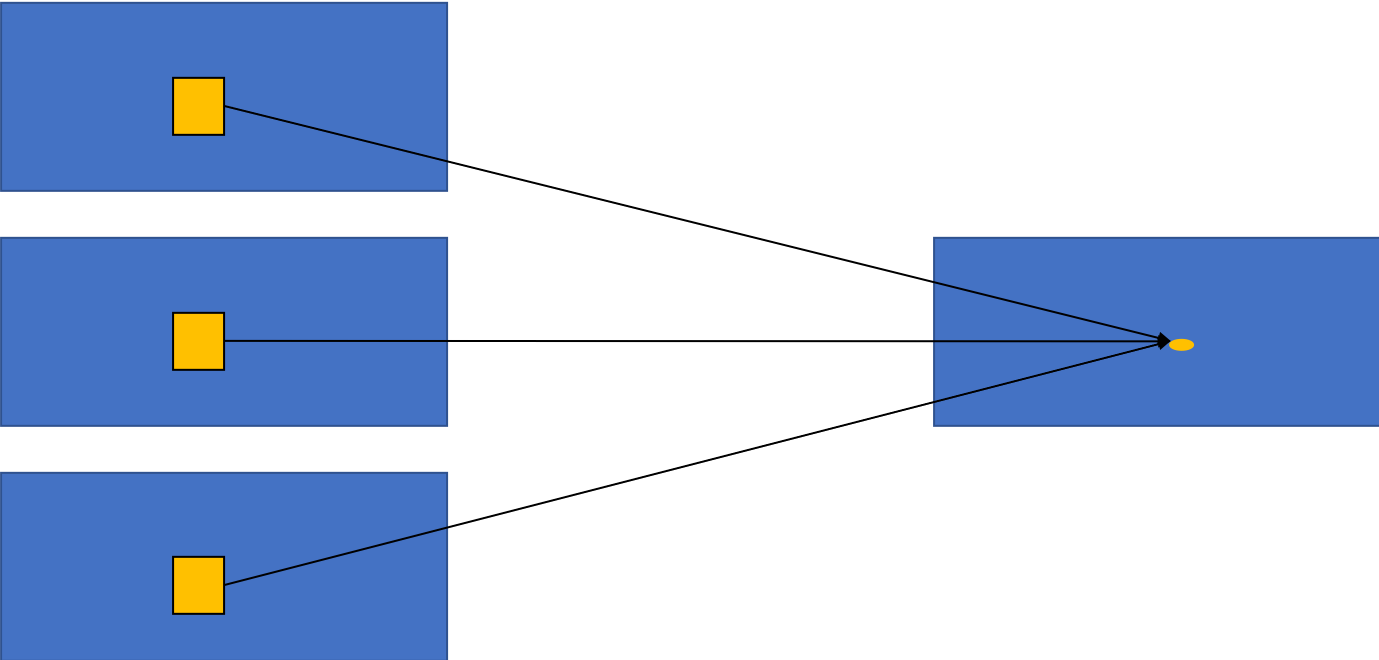
图1 2D卷积示意图

2D卷积仅仅考虑2D图片的空间信息，所以只适用于单张2D图片的视觉理解任务。在处理3D图像或视频时，网络的输入多了一个维度，输入由$(c,height,width)$ 变为了$(c,depth,height,width)$ ，其中$c$ 是通道数，$depth$为输入数据的宽度。因此，对该数据进行处理时，就需要卷积也作出相应的变换，由2D卷积变为3D卷积。

在2D卷积的基础上，3D卷积[1]被提出。3D卷积在结构上较2D卷积多了一个维度，2D卷积的尺寸可以表示为$k_h\times k_w$ ，而3D卷积的尺寸可以表示为$k_h\times k_w\times k_d$ 。3D卷积的具体的计算方式与2D卷积类似，即每次滑动时与$c$ 个通道、尺寸大小为$(depth,height,width)$ 的图像做乘加运算，从而得到输出特征图中的一个值，如 图2 所示。

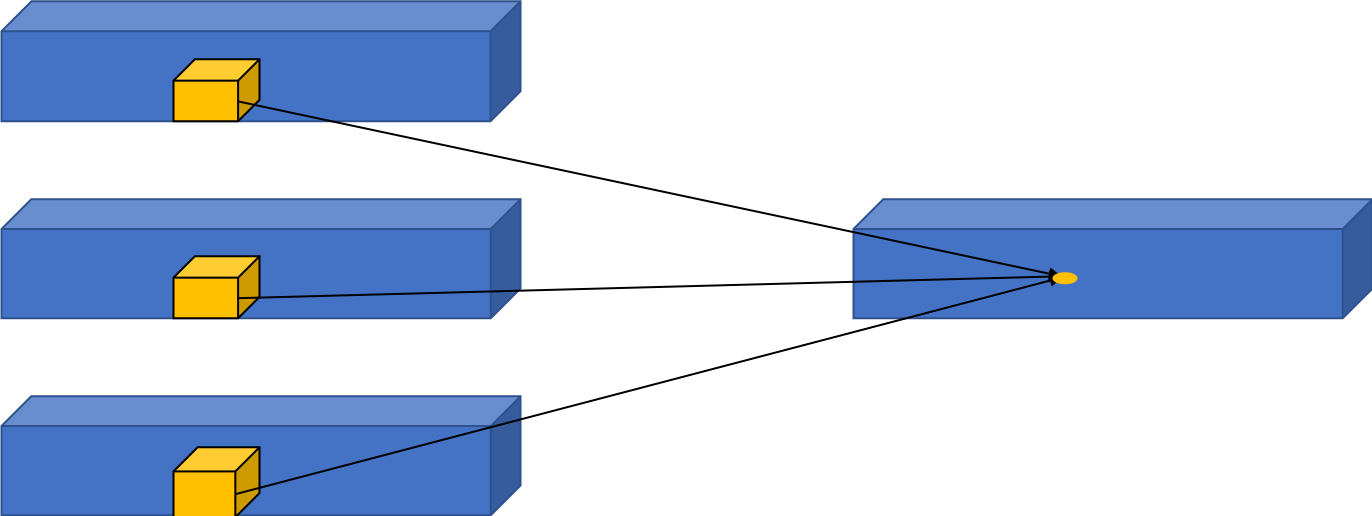
图2 3D卷积示意图

2.2 3D卷积应用示例

3D卷积的主要应用就是视频理解和医疗图像领域。

在视频理解任务中，$k_d$ 就代表了时间维度，也就是每个3D卷积核处理的连续帧数。在视频理解领域的3D卷积计算中，首先会将$k_d$ 个连续帧组成一个3D的图像序列，然后在图像序列中进行卷积计算。3D卷积核会在$k_d$ 个连续帧上进行滑动，每次滑动$k_d$ 个连续帧中对应位置内的元素都要与卷积核中的参数进行乘加计算，最后得到输出特征图中的一个值。

3D CNN中，使用了3D卷积对人体行为进行识别，网络结构如 图3 所示。网络只有3个卷积层、1个全连接层以及2个池化层。其中，前两个卷积层为3D卷积层，卷积核大小为$7\times 7\times 3$ 和$7\times 6\times 3$ ，也就是说每个卷积核处理3个连续帧中$7\times 7$ 和$7\times 6$ 大小的区域。

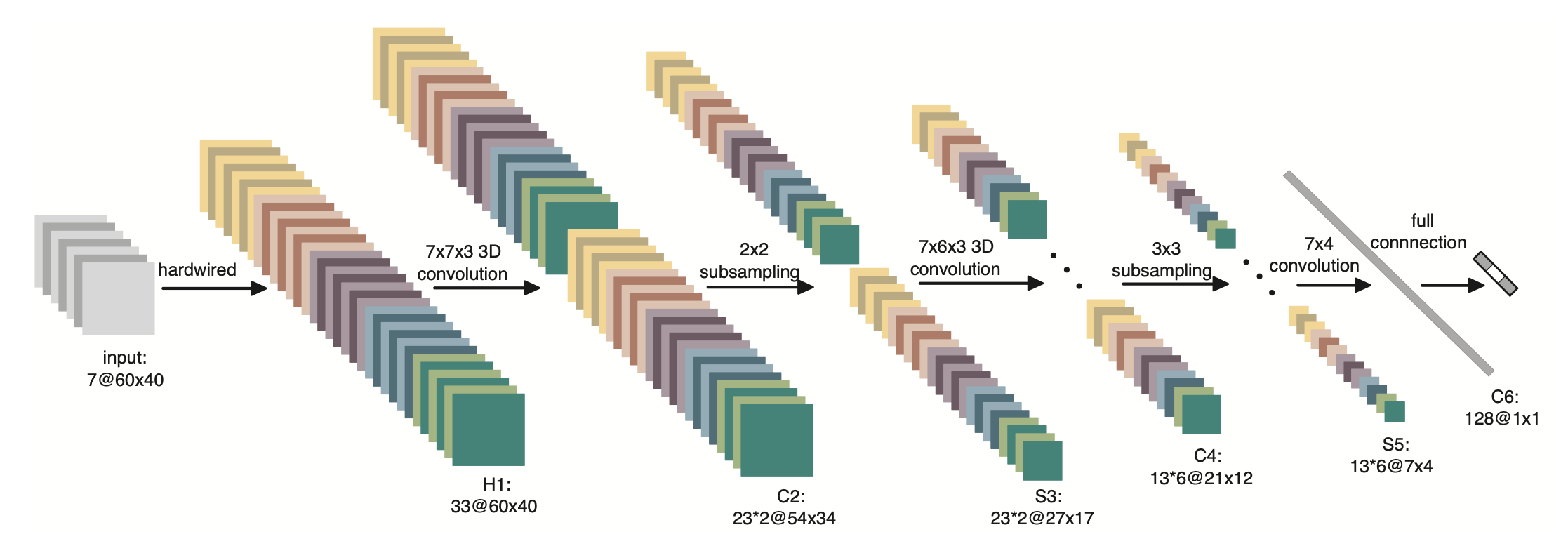
图3 3D CNN网络结构

由于该模型使用了3D卷积，使得其可以从空间和时间的维度提取特征，从而捕捉从多个连续帧中得到的运动信息。

在医疗图像领域中，医学数据通常是3D的，比如我们要分割出的肿瘤就是3D的。如果用2D的图像处理模型去处理3D物体也是可以的，但是需要将生物医学影像图片的每一个切片成组的（包含训练数据和标注好的数据）的喂给模型进行训练，在这种情况下会存在一个效率问题，因此我们使用的模型即将U-Net中2D卷积改为3D的形式，即3D U-Net[2]，如 图4 所示。

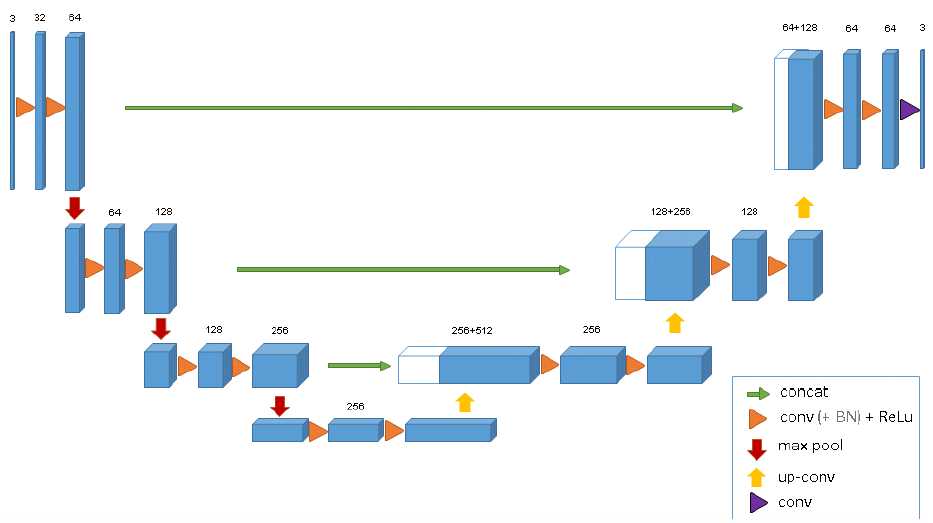
图4 3D U-Net网络结构

该模型的网络结构跟2D结构的U-Net基本一样，唯一不同就是将2D卷积操作换成了3D卷积，因此，不需要单独输入每个切片进行训练，而是可以采取输入整张图片到模型中。

参考文献
[1] 3D Convolutional Neural Networks for Human Action Recognition

[2] 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation

3.转置卷积（Transpose Convolution）

3.1 转置卷积提出背景

通常情况下，对图像进行卷积运算时，经过多层的卷积运算后，输出图像的尺寸会变得很小，即图像被约减。而对于某些特定的任务（比如：图像分割、GAN），我们需要将图像恢复到原来的尺寸再进行进一步的计算。这个恢复图像尺寸，实现图像由小分辨率到大分辨率映射的操作，叫做上采样（Upsample），如 图1 所示。

图1 上采样示例

上采样有多种方式，常见的包括：最近邻插值（Nearest neighbor interpolation）、双线性插值（Bi-Linear interpolation）等，但是这些上采样方法都是基于人们的先验经验来设计的，对于很多场景效果并不理想。因此，我们希望让神经网络自己学习如何更好地进行插值，这也就是接下来要介绍的转置卷积（Transpose Convolution）的方法。

3.2 转置卷积及其应用

转置卷积（Transpose Convolution），在某些文献中也被称为反卷积（Deconvolution）。转置卷积中，不会使用预先设定的插值方法，它具有可学习的参数，通过让网络自行学习，来获取最优的上采样方式。转置卷积在某些特定的领域有着非常广泛的应用，比如：

• 在DCGAN[1]，生成器将会用随机值转变为一个全尺寸(full-size)的图片，这个时候就需要用到转置卷积。

• 在语义分割中，会使用卷积层在编码器中进行特征提取，然后在解码层中进行恢复为原先的尺寸，这样才可以对原来图像的每个像素都进行分类。这个过程同样需要用到转置卷积。经典方法如：FCN[2]和Unet[3]。

• CNN的可视化[4]：通过转置卷积将CNN中得到的特征图还原到像素空间，以观察特定的特征图对哪些模式的图像敏感。

3.3 转置卷积与标准卷积的区别

标准卷积的运算操作其实就是对卷积核中的元素与输入矩阵上对应位置的元素进行逐像素的乘积并求和。然后使用卷积核在输入矩阵上以步长为单位进行滑动，直到遍历完输入矩阵的所有位置。

这里举一个简单的例子演示一下具体的操作过程。假设输入是一个$4\times 4$的矩阵，使用$3\times 3$的标准卷积进行计算，同时不使用填充，步长设置为1。最终输出的结果应该是一个$2\times 2$的矩阵，如 图2 所示。

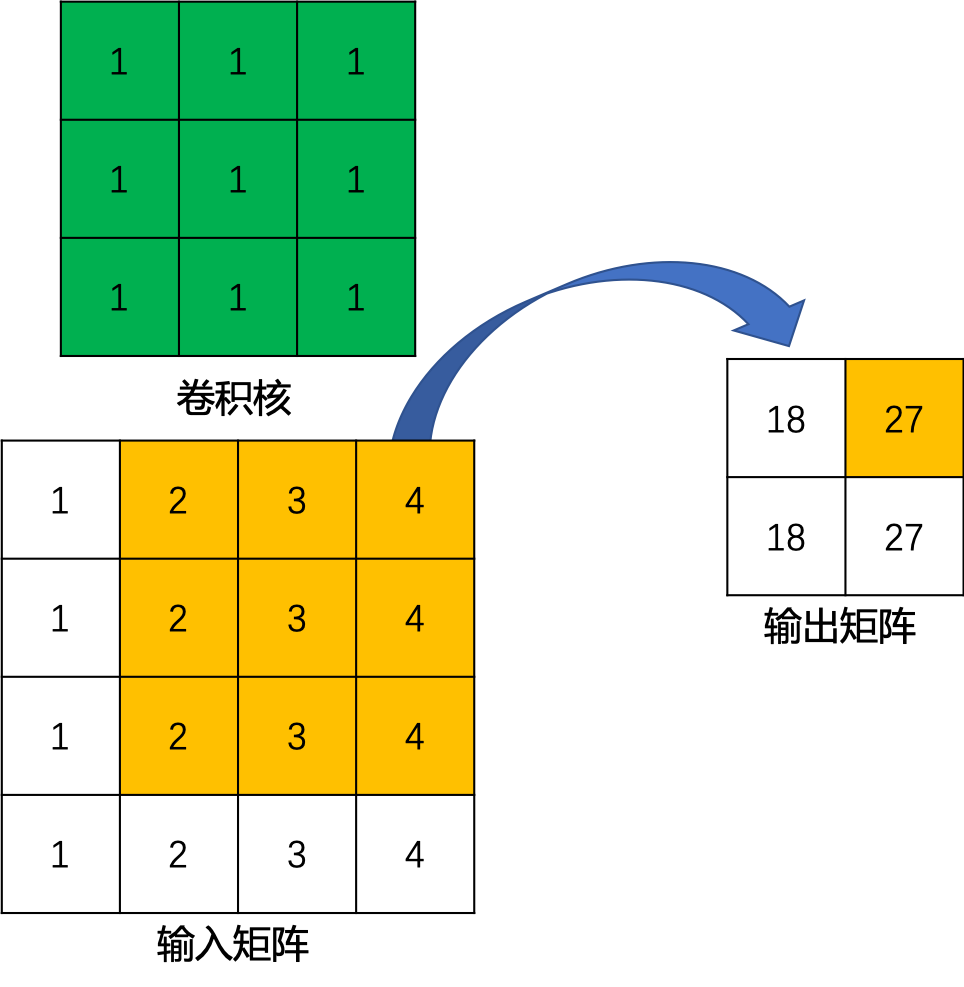
图2 标准卷积运算示例

在上边的例子中，输入矩阵右上角$3\times 3$的值会影响输出矩阵中右上角的值，这其实也就对应了标准卷积中感受野的概念。所以，我们可以说$3\times 3$的标准卷积核建立了输入矩阵中9个值与输出矩阵中1个值的对应关系。

综上所述，我们也就可以认为标准卷积操作实际上就是建立了一个多对一的关系。

对于转置卷积而言，我们实际上是想建立一个逆向操作，也就是建立一个一对多的关系。对于上边的例子，我们想要建立的其实是输出卷积中的1个值与输入卷积中的9个值的关系，如 图3 所示。

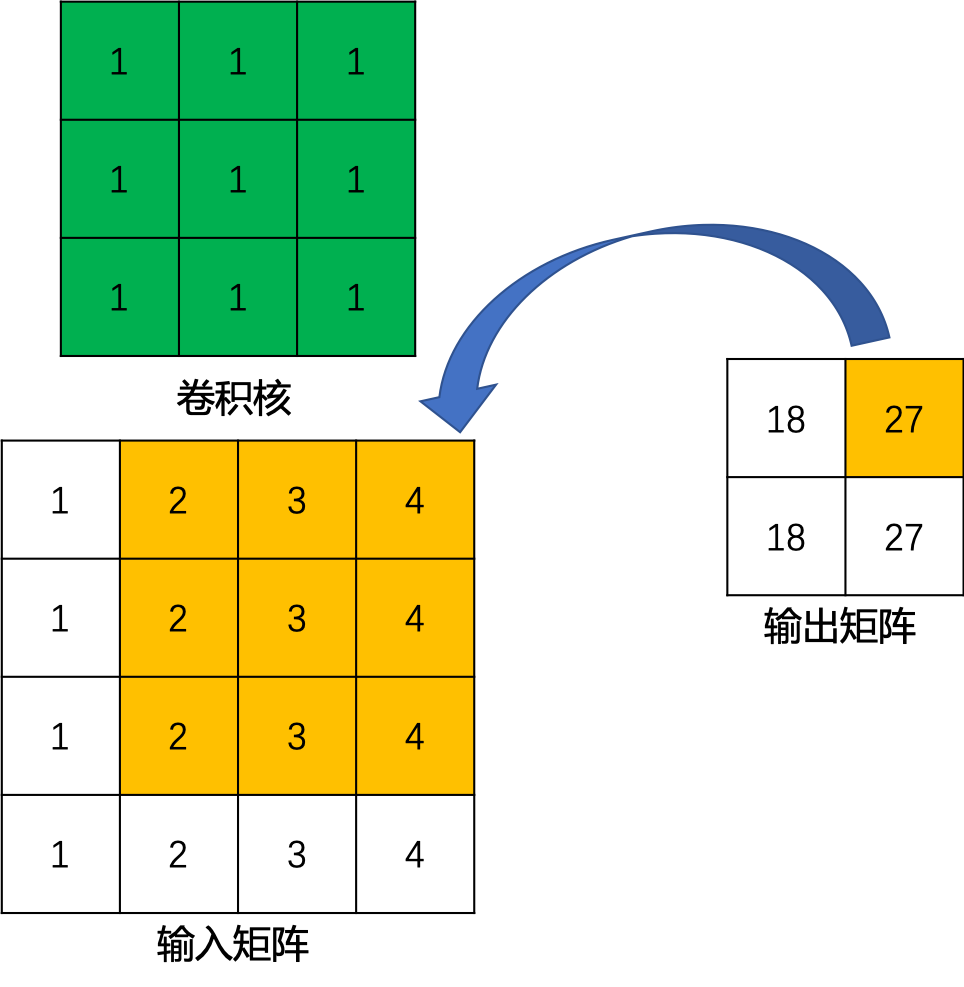
图3 卷积逆向运算示例

当然，从信息论的角度，卷积操作是不可逆的，所以转置卷积并不是使用输出矩阵和卷积核计算原始的输入矩阵，而是计算得到保持了相对位置关系的矩阵。

3.4 转置卷积数学推导

定义一个尺寸为$4\times 4$ 的输入矩阵 $input$:

$$\begin{array}{r}input=\left[\begin{array}{cccc}{x}_1& x_2& x_3& x_4\\ x_6& x_7& x_8& x_9\\ x_{10}& x_{11}& x_{12}& x_{13}\\ x_{14}& x_{15}& x_{16}& x_{17}\end{array}\right]\end{array}$$

一个尺寸为$3\times 3$ 的标准卷积核 $kernel$:

$$\begin{array}{r}kernel=\left[\begin{array}{ccc}{w}_{0,0}& w_{0,1}& w_{0,2}\\ w_{1,0}& w_{1,1}& w_{1,2}\\ w_{2,0}& w_{2,1}& w_{2,2}\end{array}\right]\end{array}$$

令步长 $stride=1$，填充$padding=0$，按照输出特征图的计算方式$o=\frac{i+2p-k}{s}+1$，我们可以得到尺寸为 $2\times 2$ 的输出矩阵 $output$ ：

$$\begin{array}{r}output=\left[\begin{array}{cc}{y}_0& y_1\\ y_2& y_3\end{array}\right]\end{array}$$

这里，我们换一个表达方式，我们将输入矩阵 $input$ 和输出矩阵 $output$ 展开成列向量$X$ 和列向量$Y$ ，那么向量$X$ 和向量$Y$ 的尺寸就分别是$16\times 1$ 和$4\times 1$，可以分别用如下公式表示：

$$\begin{array}{r}X=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\\ x_6\\ x_7\\ x_8\\ x_9\\ x_{10}\\ x_{11}\\ x_{12}\\ x_{13}\\ x_{14}\\ x_{15}\\ x_{16}\\ x_{17}\end{array}\right]\end{array}$$

$$\begin{array}{r}Y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\end{array}\right]\end{array}$$

我们再用矩阵运算来描述标准卷积运算，这里使用矩阵$C$ 来表示新的卷积核矩阵：

$$Y=CX$$

经过推导，我们可以得到这个稀疏矩阵$C$，它的尺寸为$4\times 16$：

$$\begin{array}{r}C=\left[\begin{array}{cccccccccccccccc}{w}_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0& 0\\ 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0\\ 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0\\ 0& 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}\end{array}\right]\end{array}$$

这里，我们用 图4 为大家直观的展示一下上边的矩阵运算过程。

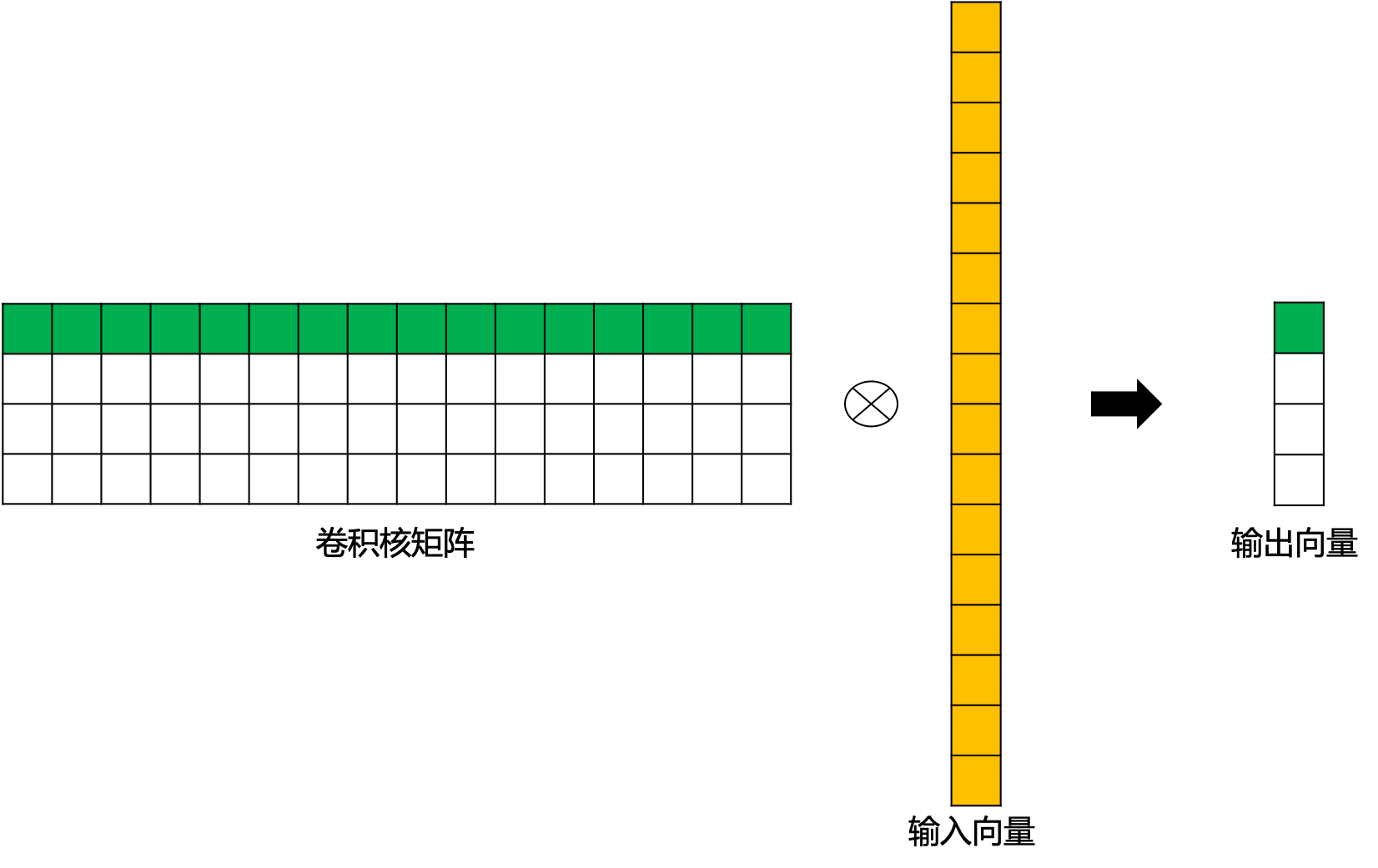
图4 标准卷积矩阵运算示例

而转置卷积其实就是要对这个过程进行逆运算，即通过 $C$ 和 $Y$ 得到 $X$ ：

$$X=C^{T}Y$$

此时，新的稀疏矩阵就变成了尺寸为$16\times 4$ 的$C^T$，这里我们通过 图5 为大家直观展示一下转置后的卷积矩阵运算示例。这里，用来进行转置卷积的权重矩阵不一定来自于原卷积矩阵. 只是权重矩阵的形状和转置后的卷积矩阵相同。

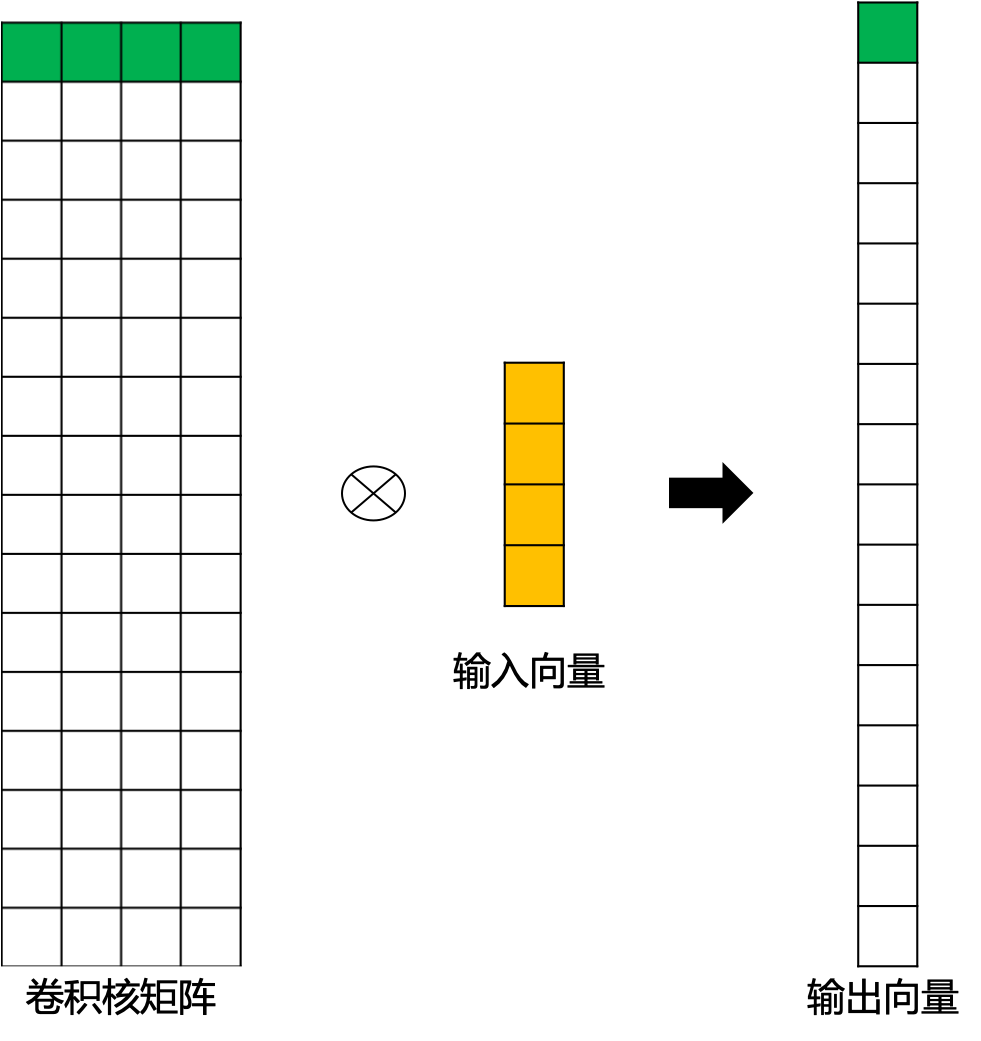
图5 转置后卷积矩阵运算示例

我们再将$16\times 1$ 的输出结果进行重新排序，这样就可以通过尺寸为$2\times 2$ 的输入矩阵得到尺寸为$4\times 4$ 的输出矩阵了。

3.5 转置卷积输出特征图尺寸

• stride=1的转置卷积

我们同样使用上文中的卷积核矩阵$C$：

$$\begin{array}{r}C=\left[\begin{array}{cccccccccccccccc}{w}_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0& 0\\ 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0& 0& 0& 0\\ 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}& 0\\ 0& 0& 0& 0& 0& w_{0,0}& w_{0,1}& w_{0,2}& 0& w_{1,0}& w_{1,1}& w_{1,2}& 0& w_{2,0}& w_{2,1}& w_{2,2}\end{array}\right]\end{array}$$

对应的输出矩阵 $output$ 为 ：

$$\begin{array}{r}output=\left[\begin{array}{cc}{y}_0& y_1\\ y_2& y_3\end{array}\right]\end{array}$$

我们将输出矩阵展开为列向量$Y$ ：

$$\begin{array}{r}Y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\end{array}\right]\end{array}$$

带入到上文中提到的转置卷积计算公式，则转置卷积的计算结果为：

$$\begin{array}{r}{C}^T{y}^{\prime }=\left[\begin{array}{cccc}{w}_{0,0}{y}_0& w_{0,1}{y}_0+w_{0,0}{y}_1& w_{0,2}{y}_0+w_{0,1}{y}_1& w_{0,2}{y}_1\\ w_{1,0}{y}_0+w_{0,0}{y}_2& w_{1,1}{y}_0+w_{1,0}{y}_1+w_{0,1}{y}_2+w_{0,0}{y}_3& w_{1,2}{y}_0+w_{1,1}{y}_1+w_{0,2}{y}_2+w_{0,1}{y}_3& w_{1,2}{y}_1+w_{0,2}{y}_3\\ w_{2,0}{y}_0+w_{1,0}{y}_2& w_{2,1}{y}_0+w_{2,0}{y}_1+w_{1,1}{y}_2+w_{1,0}{y}_3& w_{2,2}{y}_0+w_{2,1}{y}_1+w_{1,2}{y}_2+w_{1,1}{y}_3& w_{2,2}{y}_1+w_{1,2}{y}_3\\ w_{2,0}{y}_2& w_{2,1}{y}_2+w_{2,0}{y}_3& w_{2,2}{y}_2+w_{2,1}{y}_3& w_{2,2}{y}_3\end{array}\right]\end{array}$$

这其实就等价于填充 $padding=2$，输入为：

$$\begin{array}{r}input=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& y_0& y_1& 0& 0\\ 0& 0& y_2& y_3& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]\end{array}$$

同时，标准卷积核进行转置：

$$\begin{array}{r}kernel‘=\left[\begin{array}{ccc}{w}_{2,2}& w_{2,1}& w_{2,0}\\ w_{1,2}& w_{1,1}& w_{1,0}\\ w_{0,2}& w_{0,1}& w_{0,0}\end{array}\right]\end{array}$$

之后的标准卷积的结果，运算过程如 图6 所示。

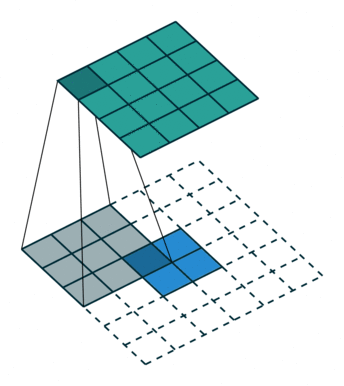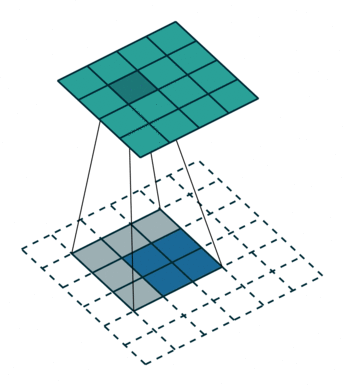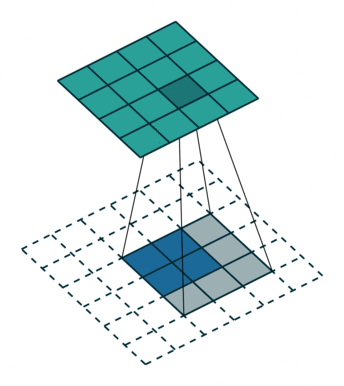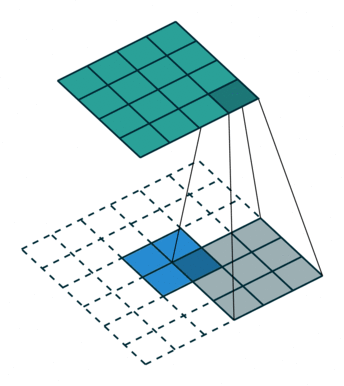
图6 s=1时，转置卷积运算示例

对于卷积核尺寸为 $k$，步长 $stride=1$，填充 $padding=0$ 的标准卷积，等价的转置卷积在尺寸为 $i^{\prime }$ 的输入矩阵上进行运算，输出特征图的尺寸 $o^{\prime }$ 为：

$$o^{\prime }=i^{\prime }+(k-1)$$

同时，转置卷积的输入矩阵需要进行 $paddin{g}^{\prime }=k-1$ 的填充。

• stride>1的转置卷积

在实际使用的过程中，我们大多数时候使用的会是stride>1的转置卷积，从而获得较大的上采样倍率。这里，我们令输入尺寸为$5\times 5$，标准卷积核的设置同上，步长 $stride=2$，填充 $padding=0$，标准卷积运算后，输出尺寸为$2\times 2$。

$$\begin{array}{r}Y=\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\end{array}\right]\end{array}$$

这里，步长$stride=2$，转换后的稀疏矩阵尺寸变为$25\times 4$，由于矩阵太大这里不展开进行罗列。则转置卷积的结果为：

$$\begin{array}{r}{C}^T{y}^{\prime }=\left[\begin{array}{ccccc}{w}_{0,0}{y}_0& w_{0,1}{y}_0& w_{0,2}{y}_0+w_{0,0}{y}_1& w_{0,1}{y}_1& w_{0,2}{y}_1\\ w_{1,0}{y}_0& w_{1,1}{y}_0& w_{1,2}{y}_0+w_{1,0}{y}_1& w_{1,1}{y}_1& w_{1,2}{y}_1\\ w_{2,0}{y}_0+w_{0,0}{y}_2& w_{2,1}{y}_0+w_{0,1}{y}_2& w_{2,2}{y}_0+w_{2,0}{y}_1+w_{0,2}{y}_2+w_{0,0}{y}_3& w_{2,1}{y}_1+w_{0,1}{y}_3& w_{2,2}{y}_1+w_{0,2}{y}_3\\ w_{1,0}{y}_2& w_{1,1}{y}_2& w_{1,2}{y}_2+w_{1,0}{y}_3& w_{1,1}{y}_3& w_{1,2}{y}_3\\ w_{2,0}{y}_2& w_{2,1}{y}_2& w_{2,2}{y}_2+w_{2,0}{y}_3& w_{2,1}{y}_3& w_{2,2}{y}_3\end{array}\right]\end{array}$$

此时，等价于输入矩阵添加了空洞，同时也添加了填充，标准卷积核进行转置之后的运算结果。运算过程如 图7 所示。

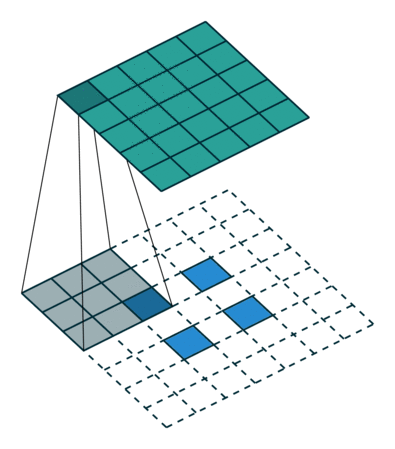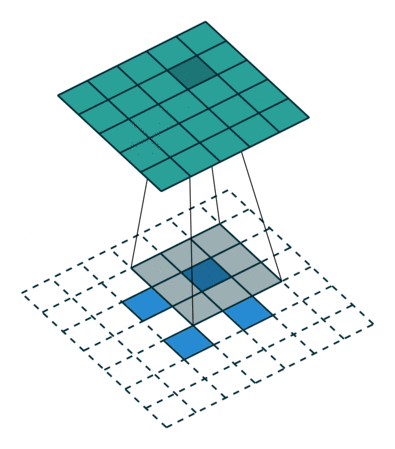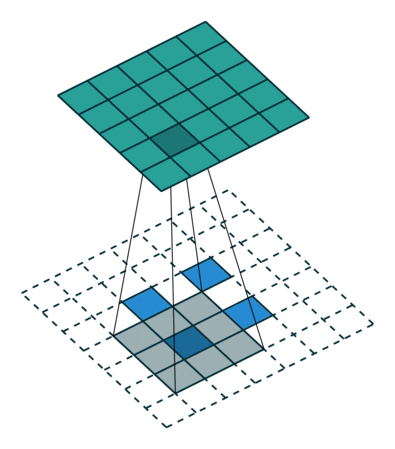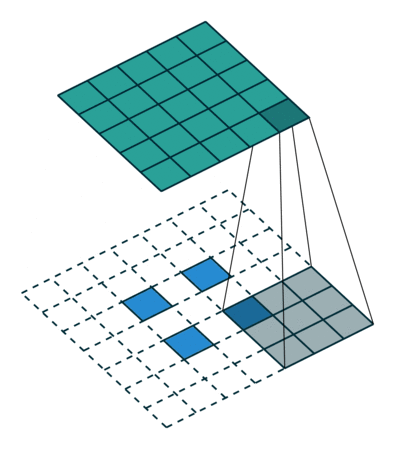
图7 s>1时，转置卷积运算示例

对于卷积核尺寸为 $k$，步长 $stride>1$，填充 $padding=0$ 的标准卷积，等价的转置卷积在尺寸为 $i^{\prime }$ 的输入矩阵上进行运算，输出特征图的尺寸 $o^{\prime }$ 为：

$$o^{\prime }=s(i^{\prime }-1)+k$$

同时，转置卷积的输入矩阵需要进行 $paddin{g}^{\prime }=k-1$ 的填充，相邻元素间的空洞大小为 $s-1$。因此，可以通过控制步长 $stride$ 来控制上采样倍率。

参考文献

[1] Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks

[2] Fully Convolutional Networks for Semantic Segmentation

[3] U-Net: Convolutional Networks for Biomedical Image Segmentation

[4] Visualizing and Understanding Convolutional Networks