来源：力扣（LeetCode）

描述：

给你二叉树的根节点 root 和一个整数 limit ，请你同时删除树中所有 不足节点 ，并返回最终二叉树的根节点。

假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit，则该节点被称之为 不足节点 ，需要被删除。

叶子节点，就是没有子节点的节点。

示例 1：

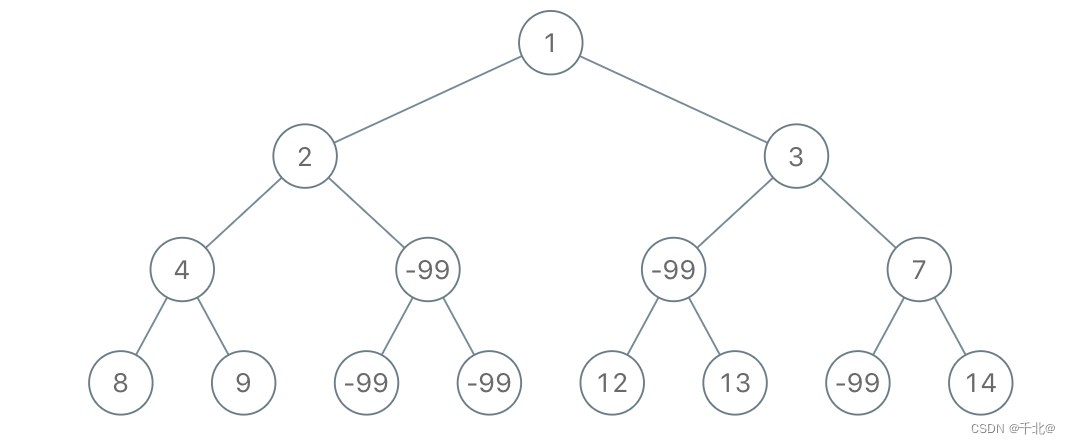
输入：root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出：[1,2,3,4,null,null,7,8,9,null,14]

示例 2：

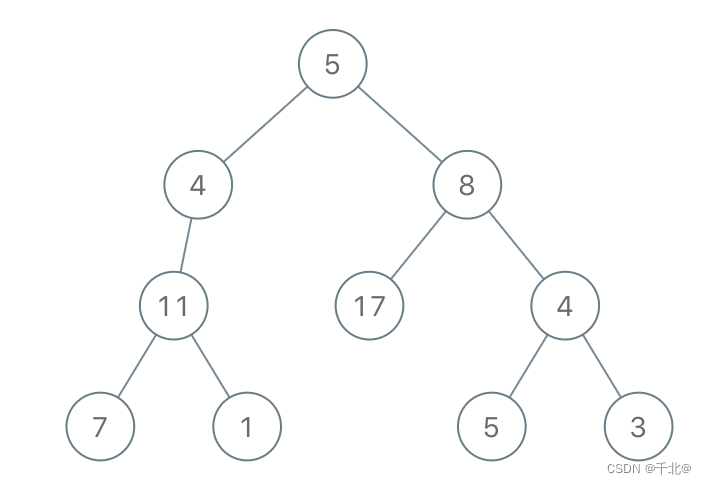
输入：root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出：[5,4,8,11,null,17,4,7,null,null,null,5]

示例 3：

输入：root = [1,2,-3,-5,null,4,null], limit = -1
输出：[1,null,-3,4]

提示：

• 树中节点数目在范围 [1, 5000] 内
• -10⁵ <= Node.val <= 10⁵
• -10⁹ <= limit <= 10⁹

方法：深度优先搜索

思路与算法

根据题意可知「不足节点」的定义为：通过节点 node 的每种可能的「根-叶」路径上值的总和全都小于给定的 limit，则该节点被称之为「不足节点」。
按照上述定义可知：

• 假设节点 node 为根的子树中所有的叶子节点均为「不足节点」，则可以推断出 node 一定也为「不足节点」，即经过该节点所有“根-叶” 路径的总和都小于 limit，此时该节点需要删除；
• 假设节点 node 为根的子树中存在叶子节点不是「不足节点」，则可以推断出 node 一定也不是「不足节点」，因为此时一定存一条从根节点到叶子节点的路径和大于等于 limit，此时该节点需要保留。

根据上述的分析，我们用 checkSufficientLeaf(node) 来检测 node 节点为子树是否含有叶子节点不为「不足节点」，每次进行深度优先搜索时并传入当前的路径和 sum，每次检测过程如下：

• 如果当前节点 node 为叶子节点，则当前 “根-叶” 路径和为 sum 加上 node 节点的值，如果当前的路径和小于 limit，则该叶子 node 一定为「不足节点」，返回 false，否则该节点一定不为「不足节点」，返回 true；
• 依次检测 node 节点的左子树与右子树，如果当前节点 node 的左子树中的叶子节点均为「不足节点」，则左孩子需要删除，否则需要保留；如果当前节点 node 的右子树中的叶子节点均为「不足节点」，则右孩子需要删除，否则需要保留。如果当前子树中的所有叶子节点均为「不足节点」则当前节点需要删除，否则当前节点需要删除。
• 最终检测 root 的叶子节点是否均为「不足节点」，如果是则返回 null，否则返回 root。

代码：

class Solution {
public:
    bool checkSufficientLeaf(TreeNode *node, int sum, int limit) {
        if (!node) {
            return false;
        }
        if (node->left == nullptr && node->right == nullptr) {
            return node->val + sum >= limit;
        }
        bool haveSufficientLeft = checkSufficientLeaf(node->left, sum + node->val, limit);
        bool haveSufficientRight = checkSufficientLeaf(node->right, sum + node->val, limit);
        if (!haveSufficientLeft) {
            node->left = nullptr;
        }
        if (!haveSufficientRight) {
            node->right = nullptr;
        }
        return haveSufficientLeft || haveSufficientRight;
    }

    TreeNode* sufficientSubset(TreeNode* root, int limit) {
        bool haveSufficient = checkSufficientLeaf(root, 0, limit);
        return haveSufficient ? root : nullptr;
    }
};

执行用时：24ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗：32.2 MB, 在所有 C++ 提交中击败了59.82%的用户
复杂度分析
时间复杂度：O(n)，其中 n 表示树中节点的数目。对于每个节点我们只需遍历一次即可，因此需要的时间复杂度为 O(n)。
空间复杂度：O(n)，其中 n 表示树中节点的数目。由于递归需要占用空间，此时空间复杂度取决于树的高度，最优情况下树的高度为 logn，此时需要的空间为 O(logn)，最差情况下树的高度为 n，此时需要的空间为 O(n)，因此空间复杂度为 O(n)。
author：LeetCode-Solution