虽然有的slam系统是代外参标定功能,可以在线标定(vins)或者离线进行标定,但外参标定的质量也会与运动激励相关的,例如对于3自由度的小车很难把z方向的外参标定的很好。有些情况车子或者是定位模块是有设计图纸的,因此通过物理方法测量的量转换成实际可行的外参或者外参的初值可以简单高效的提升标定收敛的速度已经精度。
平移外参
平移外参是一个相对比较好处理的一个值,以imu和camera的外参 t i c t_{ic} tic其物理意义是camera坐标系原点在imu坐标系的位置,因此这个量是比较容易得到的。
旋转外参
在手动计算旋转外参时候,以东北天和北东地旋转外参转换为例进行说明。形式简单可以慢慢推倒出来旋转都是90或180度这样的情况。形式复杂的一般我会采用欧拉角进行分解计算。
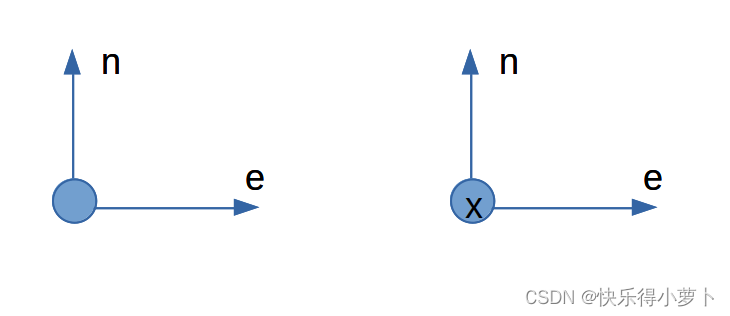
T e n u n e d T_{enu}^{ned} Tenuned东北天到北东地的转换
-
简单形式
在enu下的 [ 1 0 0 ] T \begin{matrix}[1 & 0 & 0]^T\end{matrix} [100]T 对应ned坐标系下的 [ 0 1 0 ] T \begin{matrix}[0 & 1 & 0]^T\end{matrix} [010]T
在enu下的 [ 0 1 0 ] T \begin{matrix}[0 & 1 & 0]^T\end{matrix} [010]T 对应ned坐标系下的 [ 1 0 0 ] T \begin{matrix}[1 & 0 & 0]^T\end{matrix} [100]T
在enu下的 [ 0 0 1 ] T \begin{matrix}[0 & 0 & 1]^T\end{matrix} [001]T 对应ned坐标系下的 [ 0 0 − 1 ] T \begin{matrix}[0 & 0 & -1]^T\end{matrix} [00−1]T
因此 [ 0 1 0 1 0 0 0 0 − 1 ] = R e n u n e d [ 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \end{bmatrix} = R_{enu}^{ned} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} 01010000−1 =Renuned 100010001 因此很轻松的可以推到出来
-
复杂欧拉形式
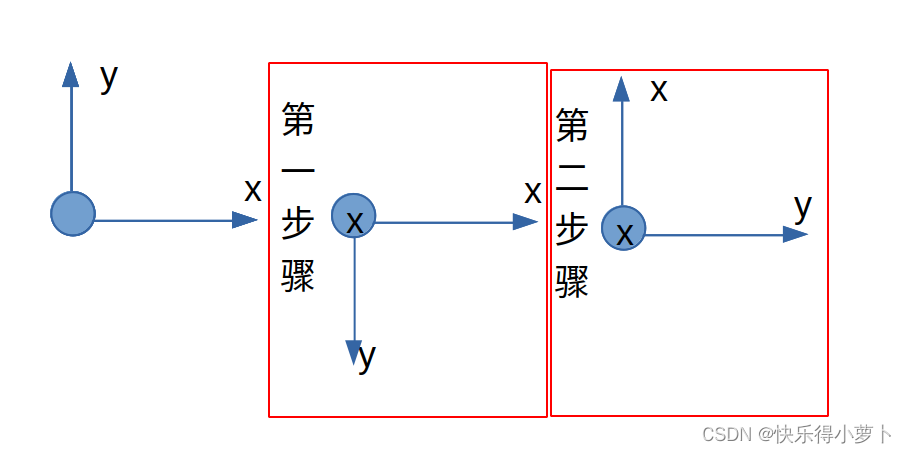
在源坐标系看第一步是沿x轴按右手顺序正转了180度,
在第一步的坐标系看第二步是沿z轴按右手顺序反转了90度
因此采用eigen中的轴角把运动合成起来
#include "iostream"
#include "eigen3/Eigen/Core"
#include "eigen3/Eigen/Geometry"
using namespace Eigen;
using namespace std;
int main(int argc, char** argv){
AngleAxisd rotX(-M_PI, Vector3d(1, 0, 0));
AngleAxisd rotY(M_PI/2., Vector3d(0, 0, 1));
std::cout << rotY.matrix()*rotX.matrix() << std::endl;
return 0;
}
结果:

与手动推倒的一致