Voigt符号

一个对称二阶张量有6个独立的分量，那么就可以将他表示成列向量的形式：

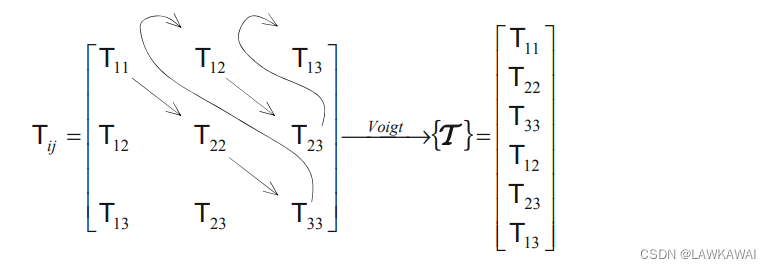
这种表示方式为Voigt符号，也可以将二阶张量表示成：

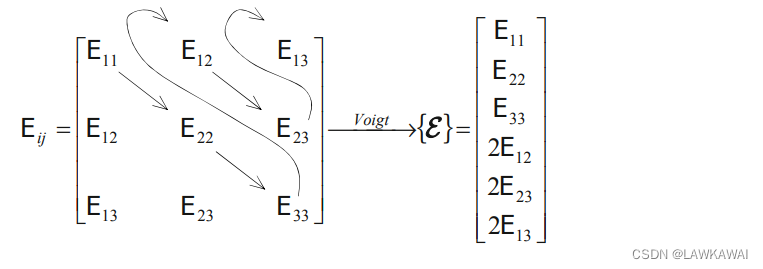
正如minor对称的四阶张量C，$C_{ijkl}=C_{jikl}=C_{ijlk}=C_{jilk}$，有$6\times 6$个独立的分量，由于ij的对称性得到了6个独立的分量，再由于kl的对称性得到6个独立的分量，可以将这36个分量表示用Voigt符号形式表示成$6\times 6$的矩阵：

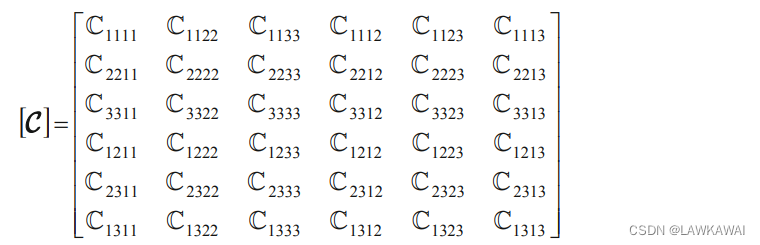
除了minor对称，还有major对称，例如$C_{ijkl}=C_{klij}$，独立的分量变成12个

一个比较简单计算矩阵[C]的分量的阶数是考虑Voigt符号形式的二阶张量的阶数

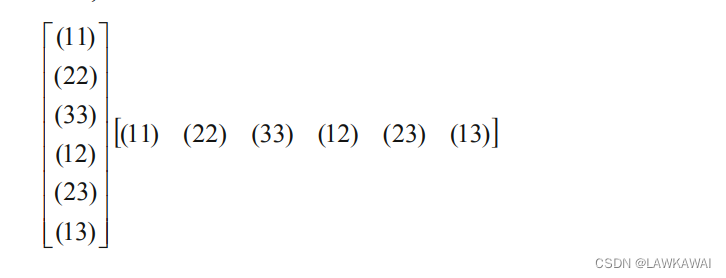
Voigt符号的单位张量

将二阶单位张量表示成Voigt符号形式：

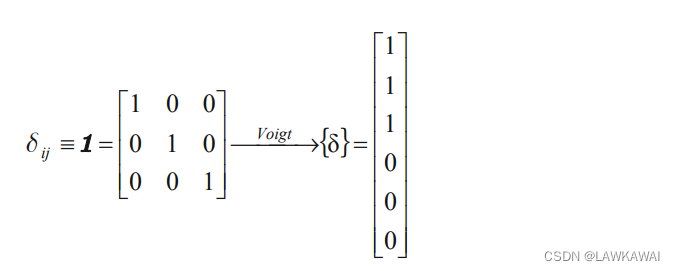
在之前的讨论中，定义了三个四阶单位张量，分别为$I_{ijkl}={\delta }_{ik}{\delta }_{jl},{\bar{I}}_{ijkl}={\delta }_{il}{\delta }_{jk},{\overline{\overline{I}}}_{ijkl}={\delta }_{ij}{\delta }_{kl}$，其中只有$ \overline{\overline I}{ijkl}=\delta{ij}\delta_{kl}$是对称的张量，那么表示Voigt符号形式的对称四阶张量：

其中${\overline{\overline{I}}}_{1111}={\delta }_{11}{\delta }_{11}=1,{\overline{\overline{I}}}_{1122}={\delta }_{11}{\delta }_{22}=1$等
一个四阶单位张量$I^{sym}$的分量，可以表示成$I_{ijkl}=\frac{1}{2}({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})$，并且Voigt符号形式为：

则上面矩阵的逆为：

Voigt符号的标量乘积

对称二阶张量T和向量$\vec{n}$的点积为$\vec{b}=T\cdot \vec{n}$，其中$\vec{b}$如下所示：

那么将二阶张量表示成Voigt符号形式，则标量乘积表示成：

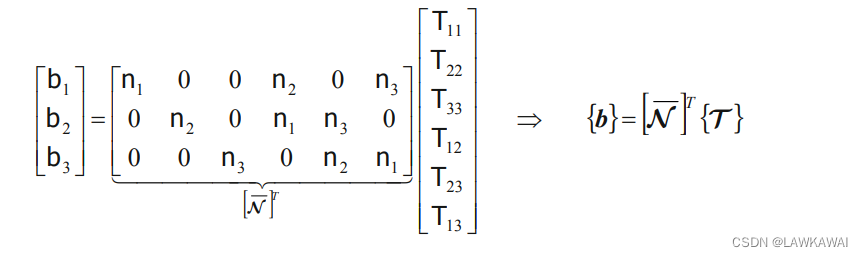
Voigt符号中的分量变换定律

二阶张量的分量变换定律：
$$T_{ij}^{\prime }=T_{kl}{a}_{ik}{a}_{jl}$$
矩阵形式：

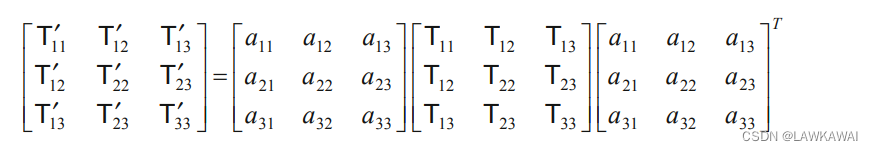
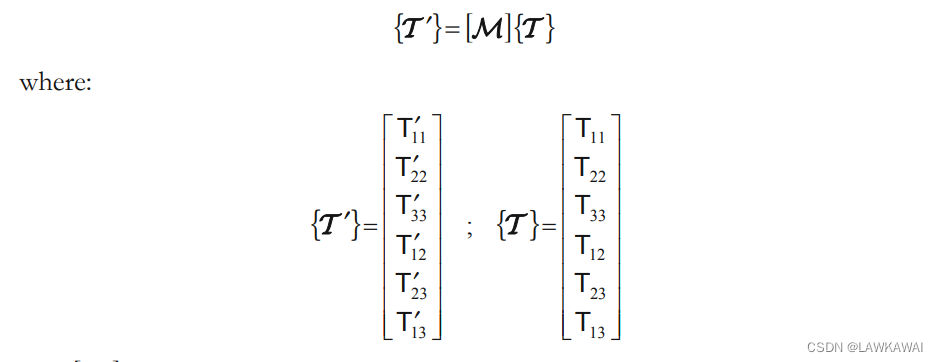
用Voigt符号形式：

其中[M]是用Voigt符号形式的二阶张量的变换矩阵，如下所示：

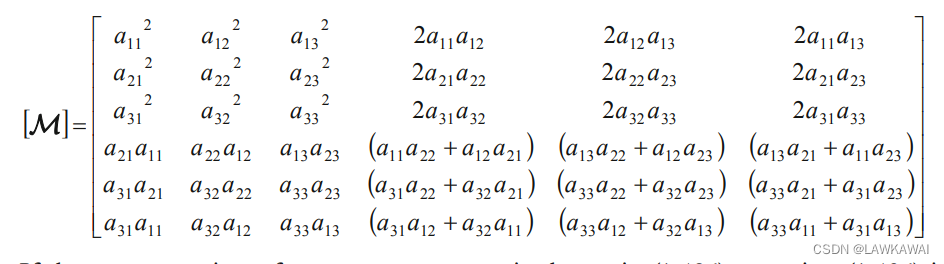
若二阶张量表示成以下Voigt符号形式：

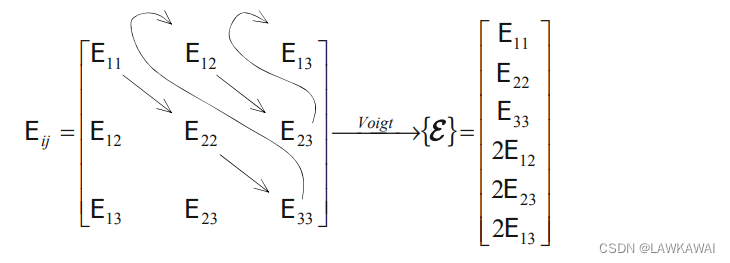
则变换矩阵为：

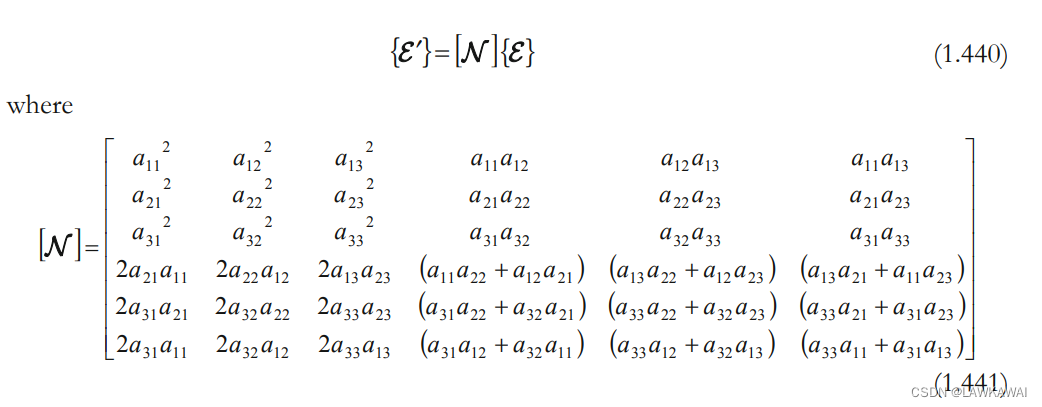
以上两个矩阵$[M]和[N]$不是正交矩阵，即$[M{]}^{-1}\ne [M{]}^T$以及$[N{]}^{-1}\ne [N{]}^T$，然而，$[M{]}^{-1}=[N{]}^T$可能成立

Voigt符号的谱表示

关于对称张量T的谱表示：

其中A是原坐标系到主空间的变换矩阵，由特征向量${\hat{n}}^{(a)}$构成，以上方程可以写成：

Viogt符号形式的二阶张量的谱表示为：

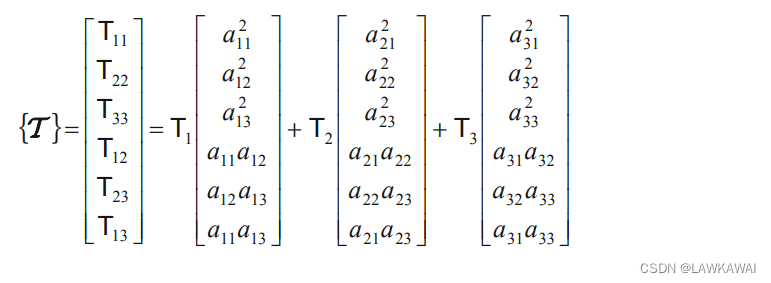
Voigt符号的

偏张量的分量：

$T_{ij}^{dev}$的Voigt符号形式：

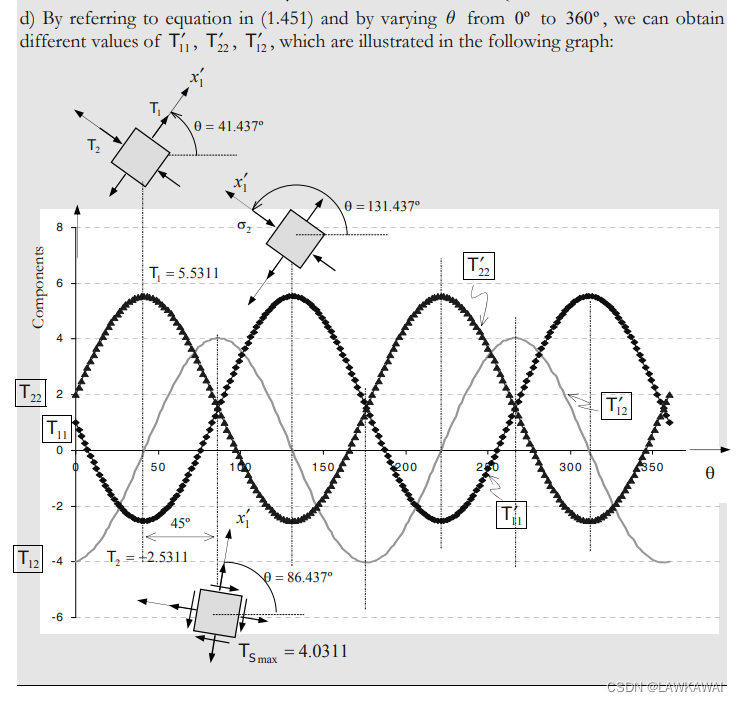
问题1.40 $T(\vec{x},t)$是一个对称二阶张量，用位置$\vec{x}$和时间t表示，并且张量沿着$x_3$方向的分量等于0，例如$T_{13}=T_{23}=T_{33}=0$

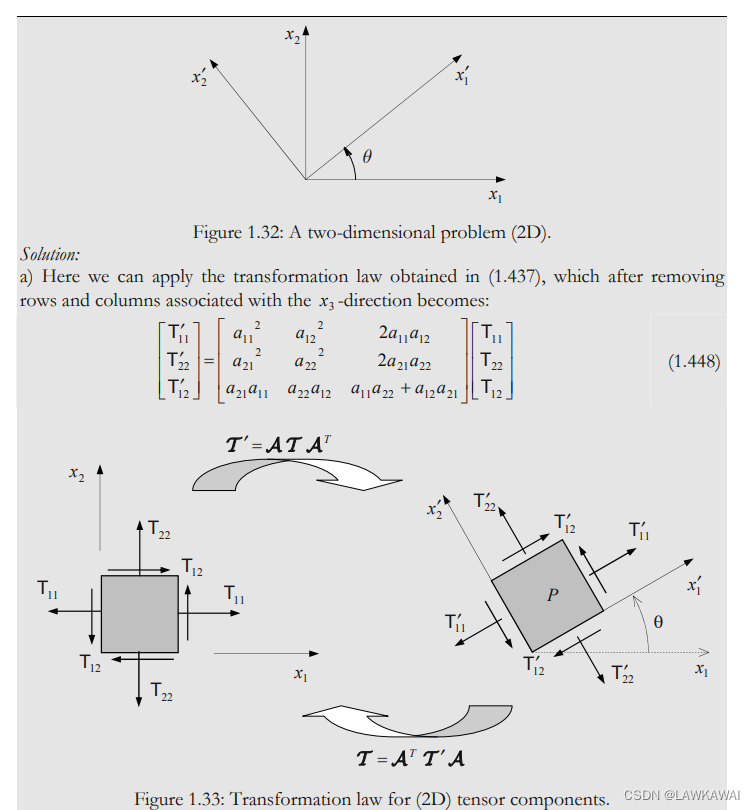
参考教材：
Eduardo W.V. Chaves， Notes On Continuum Mechanics