1. 解决了什么问题?
对于低成本自动驾驶系统,仅凭视觉信息进行 3D 目标检测是非常有挑战性的。目前的多相机 3D 目标检测方法有两类,一类直接对单目图像做预测,没有考虑 3D 场景的结构或传感器配置。这类方法需要多步后处理,融合不同相机输出的预测结果,去除冗余边框。另一类方法则使用了 3D 重建,从图像信息构造 pseudo-LiDAR 数据或场景的深度信息,然后应用 3D 目标检测方法。但是这类方法会面临复合性错误,若深度信息估计错了,则 3D 目标检测就会很受影响。
2. 提出了什么方法?
本方法针对 2D 现有信息和 3D 预测任务提出了一个 top-down 的方案,不需要预测深度信息。它从多个相机的图像中提取 2D 特征,使用一组稀疏的 3D object queries 索引 2D 特征,通过相机变换矩阵将 3D 坐标和多视角图像关联起来。对每个 object query 都会预测一个边框,然后使用 set-to-set 损失函数计算预测框和 ground-truth 的距离。
本方法包括 3 个部分。
- 首先是一个 ResNet 主干网络,用于提取特征。
- 其次是一个检测 head,通过几何的方式将 2D 特征和 3D 边框预测联系起来。每个 object query 编码一个 3D 坐标,映射到相机平面,通过双线性插值获取图像特征。然后使用 multi-head attention 层计算目标之间的关系,再用于优化 object queries。这一层会重复多次,交替地采样特征和优化 object query。
- 最后计算一个 set-to-set 损失,训练网络。

2.1 特征学习
模型的输入是一个图像集合, I = { im 1 , . . . , im K } ⊂ R H i m × W i m × 3 \mathcal{I}=\lbrace \text{im}_1,...,\text{im}_K \rbrace \subset \mathbb{R}^{H_{im}\times W_{im}\times 3} I={im1,...,imK}⊂RHim×Wim×3,相机参数矩阵 T = { T 1 , . . . , T K } ⊂ R 3 × 4 \mathcal{T}=\lbrace T_1,...,T_K \rbrace \subset \mathbb{R}^{3\times 4} T={T1,...,TK}⊂R3×4,ground-truth 边框 B ⊂ { b 1 , . . . , b j , . . . , b M } ⊂ R 9 \mathcal{B}\subset \lbrace b_1,...,b_j,...,b_M \rbrace \subset \mathbb{R}^9 B⊂{b1,...,bj,...,bM}⊂R9,以及类别标签 C ⊂ { c 1 , . . . , c j , . . . , c M } ⊂ Z \mathcal{C}\subset \lbrace c_1,...,c_j,...,c_M \rbrace \subset \mathbb{Z} C⊂{c1,...,cj,...,cM}⊂Z。每个 b j b_j bj包括鸟瞰视角(BEV)的位置、大小、航向角、速度。模型从图像中预测出它们的边框和标签。
使用了一个 ResNet 和 FPN 来编码这些图像特征,得到 4 个特征集合 F 1 , F 2 , F 3 , F 4 \mathcal{F}_1,\mathcal{F}_2,\mathcal{F}_3,\mathcal{F}_4 F1,F2,F3,F4。每个集合 F k = { f k 1 , . . . , f k 6 } ⊂ R H × W × C \mathcal{F}_k=\lbrace f_{k1},...,f_{k6}\rbrace \subset \mathbb{R}^{H\times W\times C} Fk={fk1,...,fk6}⊂RH×W×C对应 6 张输入图像的一个特征层级。这些多尺度信息为识别不同大小的目标提供了丰富的信息。
2.2 检测 Head
DETR3D 是迭代进行的,从 2D 特征图上预测边框,共有 L L L层。每一层的操作如下:
- 关于 object queries 预测一组 3D 边框中心点坐标;
- 通过相机变换矩阵,将这些中心点映射到特征图上;
- 通过双线性插值采样特征,并融入 object queries;
- 用 multi-head attention 计算出目标之间的关系。
每一层
l
∈
{
0
,
.
.
.
,
L
−
1
}
\mathcal{l}\in \lbrace 0,...,L-1 \rbrace
l∈{0,...,L−1}都在一个 object queries 集合
Q
l
=
{
q
l
1
,
.
.
.
,
q
l
M
∗
}
⊂
R
C
\mathcal{Q}_l=\lbrace q_{l1},...,q_{lM^*} \rbrace \subset \mathbb{R}^C
Ql={ql1,...,qlM∗}⊂RC上操作,输出一个新的集合
Q
l
+
1
\mathcal{Q}_{l+1}
Ql+1。从 object query
q
l
i
q_{li}
qli解码出一个 reference point
c
l
i
∈
R
3
c_{li}\in \mathbb{R}^3
cli∈R3:
c
l
i
=
Φ
ref
(
q
l
i
)
c_{li}=\Phi^{\text{ref}}(q_{li})
cli=Φref(qli)
其中
Φ
ref
\Phi^{\text{ref}}
Φref是一个神经网络。
c
l
i
c_{li}
cli可以假定为 第
i
i
i个边框的中心点。接下来,通过相机矩阵,将
c
l
i
c_{li}
cli映射到图像上:
c
l
i
∗
=
c
l
i
⊕
1
c
l
m
i
=
T
m
c
l
i
∗
c_{li}^*=c_{li}\oplus 1\quad \quad c_{lmi}=T_m c^*_{li}
cli∗=cli⊕1clmi=Tmcli∗
⊕ \oplus ⊕表示 concat, c l m i c_{lmi} clmi是 reference point 映射到第 m m m个相机画面的位置,对其做了归一化 c l m i ∈ [ − 1 , 1 ] c_{lmi}\in [-1,1] clmi∈[−1,1]。通过双线性插值获取图像特征:
f l k m i = f bilinear ( F k m , c l m i ) f_{lkmi}=f^{\text{bilinear}}(\mathcal{F}_{km},c_{lmi}) flkmi=fbilinear(Fkm,clmi)
f
l
k
m
i
f_{lkmi}
flkmi是第
l
l
l个网络层、第
m
m
m个相机、第
i
i
i个引用点、第
k
k
k个特征层的特征。
一个 reference point 并不会出现在所有的相机画面中,我们需要过滤掉无效的点。根据 reference point 是否映射到某图像平面之外,定义了一个 binary value
σ
l
k
m
i
\sigma_{lkmi}
σlkmi。
f l i = 1 ∑ k ∑ m σ l k m i + ϵ ∑ k ∑ m f l k m i σ l k m i and q ( l + 1 ) i = f l i + q l i f_{li}=\frac{1}{\sum_k \sum_m \sigma_{lkmi}+\epsilon}\sum_k \sum_m f_{lkmi}\sigma_{lkmi} \quad \text{and} \quad q_{(l+1)i} = f_{li} + q_{li} fli=∑k∑mσlkmi+ϵ1k∑m∑flkmiσlkmiandq(l+1)i=fli+qli
ϵ \epsilon ϵ防止除数为0。最终,对于每个 q l i q_{li} qli,用神经网络 Φ l reg \Phi_l^{\text{reg}} Φlreg和 Φ l cls \Phi_l^{\text{cls}} Φlcls预测一个边框 b ^ l i \hat{b}_{li} b^li和类别标签 c ^ l i \hat{c}_{li} c^li:
b ^ l i = Φ l reg ( q l i ) and c ^ l i = Φ l cls ( q l i ) \hat{b}_{li}=\Phi_l^{\text{reg}}(q_{li}) \quad \text{and}\quad \hat{c}_{li}=\Phi_l^{\text{cls}}(q_{li}) b^li=Φlreg(qli)andc^li=Φlcls(qli)
训练时,计算每一层预测的边框 B ^ l = { b ^ l 1 , . . . , b ^ l j , . . . , b ^ l M ∗ } ⊂ R 9 \hat{\mathcal{B}}_l=\lbrace \hat{b}_{l1},...,\hat{b}_{lj},...,\hat{b}_{lM^*} \rbrace\subset \mathbb{R}^9 B^l={b^l1,...,b^lj,...,b^lM∗}⊂R9和 C ^ l = { c ^ l 1 , . . . , c ^ l j , . . . , c ^ l M } ⊂ Z \hat{\mathcal{C}}_l=\lbrace \hat{c}_{l1},...,\hat{c}_{lj},...,\hat{c}_{lM} \rbrace \subset \mathbb{Z} C^l={c^l1,...,c^lj,...,c^lM}⊂Z。推理时,只使用最后一层的输出。
2.3 Loss
使用了 set-to-set 损失来计算预测集合 ( B ^ l , C ^ l ) (\hat{\mathcal{B}}_l, \hat{\mathcal{C}}_l) (B^l,C^l)和 ground-truth 集合 ( B , C ) (\mathcal{B},\mathcal{C}) (B,C)的距离。损失包括两个部分:类别标签的 focal loss、边框回归的 L 1 L_1 L1损失。Ground-truth 边框个数 M M M一般要小于预测框的个数 M ∗ M^* M∗,用 ∅ \varnothing ∅来补充 ground-truth 集合,使其元素个数等于 M ∗ M^* M∗。通过二分匹配,在 ground-truth 和预测框之间建立对应关系: σ ∗ = arg min σ ∈ P ∑ j = 1 M − I { c j ≠ ∅ } p ^ σ ( j ) ( c j ) + I { c j ≠ ∅ } L b o x ( b j , b ^ σ ( j ) ) \sigma^* = \argmin_{\sigma\in\mathcal{P}} \sum_{j=1}^M -\mathbb{I}_{\lbrace c_j\neq \varnothing \rbrace} \hat{p}_{\sigma(j)}(c_j) + \mathbb{I}_{\lbrace c_j\neq\varnothing \rbrace}\mathcal{L}_{box}(b_j, \hat{b}_{\sigma(j)}) σ∗=argminσ∈P∑j=1M−I{cj=∅}p^σ(j)(cj)+I{cj=∅}Lbox(bj,b^σ(j)), P \mathcal{P} P表示所有排列组合的集合, p ^ σ ( j ) ( c j ) \hat{p}_{\sigma(j)}(c_j) p^σ(j)(cj)是索引为 σ ( j ) \sigma(j) σ(j)的预测框类别是 c j c_j cj的概率。 L b o x \mathcal{L}_{box} Lbox是边框的 L 1 L_1 L1损失。使用 Hungarian 算法解决这个分配问题,得到 set-to-set 损失:
L s u p = ∑ j = 1 N [ − log p ^ σ ∗ ( j ) ( c j ) + I { c j ≠ ∅ } L b o x ( b j , b ^ σ ∗ ( j ) ) ] \mathcal{L}_{sup}=\sum_{j=1}^N\left[ -\log \hat{p}_{\sigma^*(j)}(c_j) + \mathbb{I}_{\lbrace c_j\neq\varnothing \rbrace} \mathcal{L}_{box}(b_j, \hat{b}_{\sigma^*(j)})\right] Lsup=j=1∑N[−logp^σ∗(j)(cj)+I{cj=∅}Lbox(bj,b^σ∗(j))]
2.4 实验
2.4.1 数据集
作者使用了 nuScenes 数据集,包括 1000 个帧序列,每个序列约 20 秒,帧率是 20 FPS。每个样本包括从 6 个相机采集的画面 [front left, front, front right, back left, back, back right]。nuScenes 提供了相机的内参和外参。每 0.5 秒提供一个标注,总共有 2.8 万个训练样本、6000 个验证样本、6000 个测试样本。
2.4.2 Metrics
使用的 nuScenes 官方评价标准: average translation error (ATE), average scale error (ASE), average orientation error (AOE), average velocity error (AVE), 以及 average attribute error (AAE)。这些度量都是 true positive metrics(TP metrics),nuScenes 提供了 nuScenes Detection Score(NDS):
NDS
=
1
10
[
5
mAP
+
∑
mTP
∈
T
P
(
1
−
min
(
1
,
mTP
)
)
]
\text{NDS}=\frac{1}{10}\left[ 5\text{mAP} + \sum_{\text{mTP}\in \mathbb{TP}}(1-\min(1, \text{mTP})) \right]
NDS=101[5mAP+mTP∈TP∑(1−min(1,mTP))]
2.4.3 Model
包括一个 ResNet-101、一个 FPN、一个 DETR3D 检测 head。在 ResNet-101 的第 3 和第 4 阶段,使用了 deformable conv。FPN 输出 4 个特征图,大小分别是输入图像大小的 1 / 8 , 1 / 16 , 1 / 32 1/8,1/16,1/32 1/8,1/16,1/32和 1 / 64 1/64 1/64。DETR3D 检测 head 有 6 层,每一层都由一个特征优化步骤和一个 multi-head 注意力层组成。DETR3D 检测 head 的隐藏维度是 256。最后是两个子网络,分别预测每个 object query 的边框的坐标信息和类别标签,每个子网络包含 2 个全连接层,隐藏层维度是 256。在检测 head 中也使用了 layer norm。
2.4.4 训练
训练时使用 AdamW 策略,weight decay 是 1 0 − 4 10^{-4} 10−4,初始学习率是 1 0 − 4 10^{-4} 10−4,在第 8 和第 11 个 epoch 学习率降为 1 0 − 5 10^{-5} 10−5和 1 0 − 6 10^{-6} 10−6。在 8 张 3090 GPUs 上总共训练 12 个 epochs,mini-batch 为 1。
2.4.5 分析
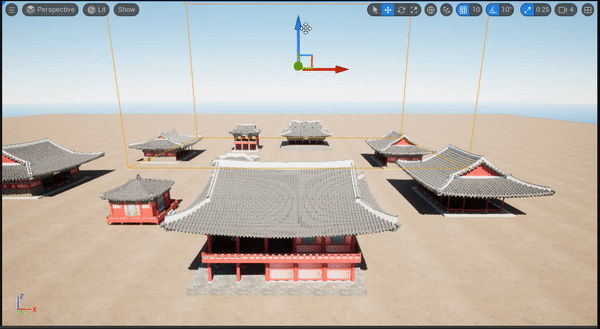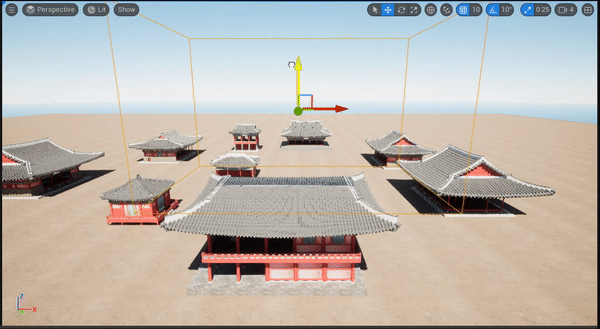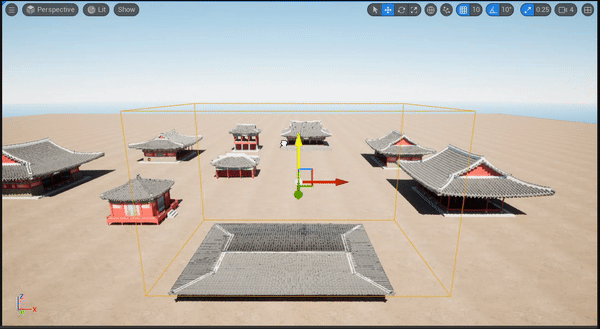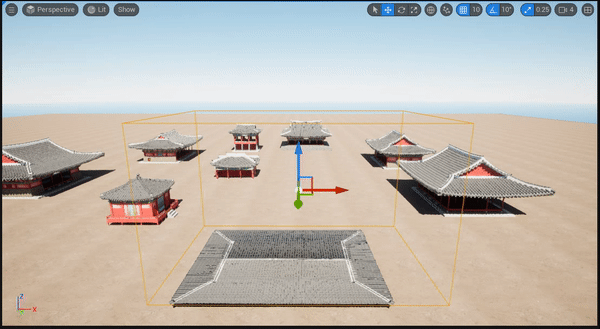
下图中,作者可视化了每一层中 object queries 解码出的边框。随着层越来越深,预测边框越来越接近 ground-truth 框,证明迭代式的优化策略能大幅度提升检测表现。

如下图所示,作者将预测边框投影到相机画面和 BEV 视角。本方法能够给出合理的结果,甚至能检测出小目标。

3. 有什么优点?
- 本方法无需根据图像信息进行点云重建或者深度估计,对深度预测造成的错误更加鲁棒。
- 本方法无需任何后处理步骤如 NMS。
- 在多相机的重叠区域,本方法显著优于其它方案。
4. 有什么问题?
DETR3D 从 2D 到 3D 的变换可能带来严重的问题:
- 预测的 reference point 坐标可能不够准确,采样的特征位于目标区域之外;
- 只有映射点附近的特征会被选取,无法从全局角度学习特征;
- 特征采样过程复杂,使检测器很难应用。
因此构建一个端到端的、无需 2D 到 3D 变换的 3D 目标检测框架仍是一个问题。









![[MAUI]在.NET MAUI中复刻苹果Cover Flow](https://img-blog.csdnimg.cn/427db839c6b7434aa54ecba60c5325f8.gif)