【数据结构】--- 博主拍了拍你并向你扔了一“堆”二叉树(堆的概念+结构+代码实现)

news2024/10/7 4:33:48

文章目录

  • 前言
  • 🌟一、二叉树的顺序结构及实现：
  • 🌟二、堆的概念及结构：
  • 🌟三、堆的代码实现：
    • 🌏3.1 堆的创建：
    • 🌏3.2 堆的结构：
    • 🌏3.3 初始化：
    • 🌏3.4 堆的插入：
      • 💫3.4.1 堆向上调整算法：
        • 📝3.4.1.1 代码(以小堆为例)：
        • 📝3.4.1.2 流程图：
      • 💫3.4.2 堆向上调整算法(插入)：
    • 🌏3.5 堆的删除(删除堆顶元素)：
      • 💫3.5.1 堆向下调整算法：
        • 📝3.5.1.1 代码(以小堆为例)：
        • 📝3.5.1.2 流程图：
      • 💫3.5.2 堆向下调整算法(删除)：
    • 🌏3.6 堆的堆顶数据：
    • 🌏3.7 堆的堆数据个数：
    • 🌏3.8 判空：
    • 🌏3.9 释放：
  • 🌟四、堆实现的完整代码：
  • 🌟五、堆伏笔：
  • 😽总结

前言

👧个人主页：@小沈熬夜秃头中୧⍤⃝❅
😚小编介绍：欢迎来到我的乱七八糟小星球🌝
📋专栏：数据结构
🔑本章内容：二叉树—堆
送给各位💌：心有所期全力以赴定有所成.
记得 评论📝 +点赞👍 +收藏😽 +关注💞哦~

提示：以下是本篇文章正文内容，下面案例可供参考

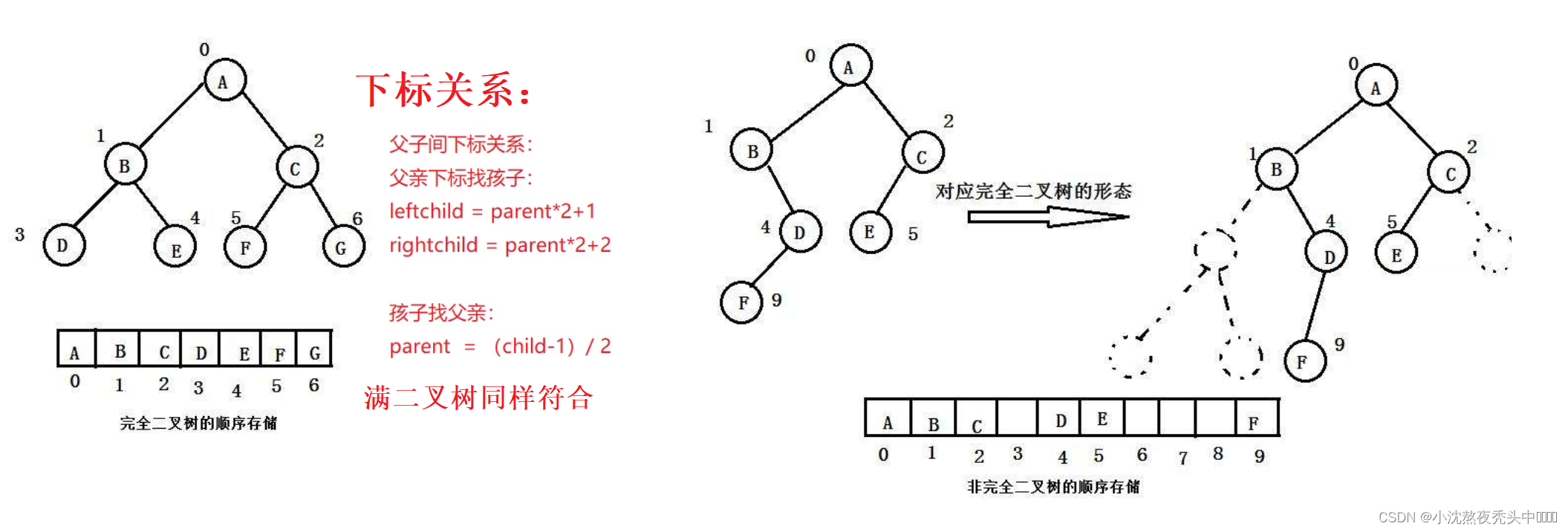
🌟一、二叉树的顺序结构及实现：

请添加图片描述
请添加图片描述

🌟二、堆的概念及结构：

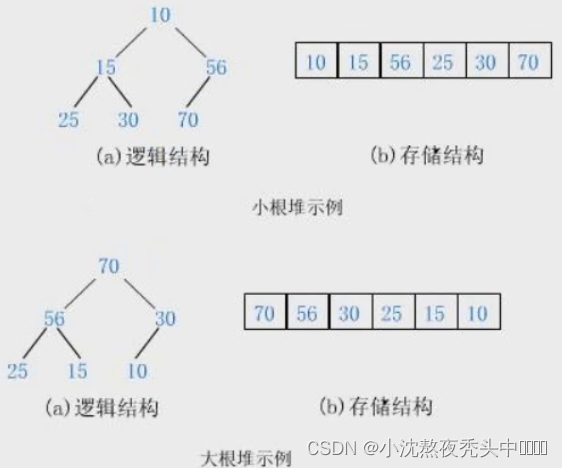
如果有一个关键码的集合K = { ， ， ，…， }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足： <= 且 <= ( >= 且 >= ) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质:

  • 完全二叉树
  • 大堆:树任何一个父亲都大于或等于孩子
  • 小堆:树任何一个父亲都小于或等于孩子

请添加图片描述

🌟三、堆的代码实现：

对于堆的代码实现无非就是先定义结构，包括 初始化 插入 删除堆顶元素 堆顶数据 堆数据个数 判空 释放

🌏3.1 堆的创建：

下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的子树开始调整，一直调整到根节点的树，就可以调整成堆。

🌏3.2 堆的结构：

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);

🌏3.3 初始化：

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

🌏3.4 堆的插入：

💫3.4.1 堆向上调整算法：

向堆中插入数据，需要使用向上调整算法调整，因为向堆中插入数据是将数据插入到下标为size的位置，此时就不满足小堆 (大堆)，因此，需要堆其进行调整，向上调整算法和向下调整算法思路类似，此处以小堆为例，向上调整法只需从插入的节点位置开始和父节点比较。

📝3.4.1.1 代码(以小堆为例)：

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])
		{
			HPDataType tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

📝3.4.1.2 流程图：

在这里插入图片描述

💫3.4.2 堆向上调整算法(插入)：

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	AdjustUp(php->a, php->size);//堆向上调整算法
	php->size++;
}

🌏3.5 堆的删除(删除堆顶元素)：

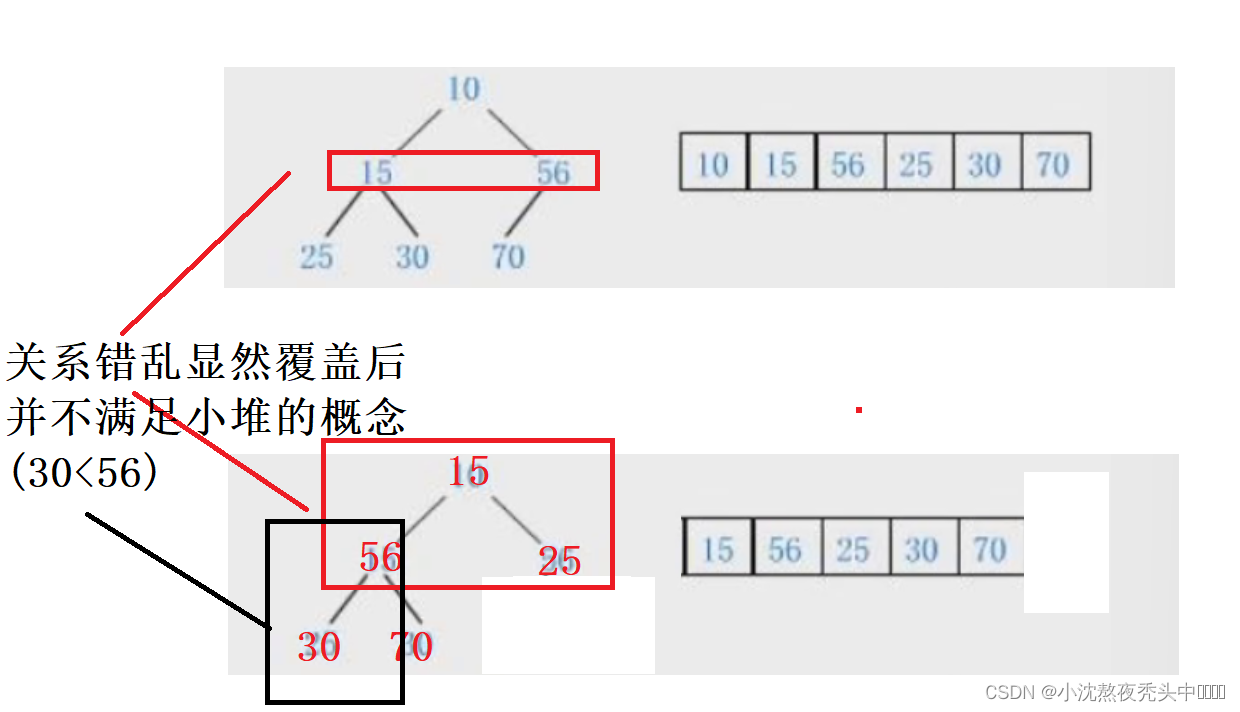
对于堆顶元素的删除，可能想到了覆盖，但是覆盖显然是不太满足的因为当我们删除堆顶元素本来关系为兄弟的节点就变成了父子等导致关系错乱(一旦关系错乱就导致不满足大堆/小堆中双亲与子孙的关系—小堆为例双亲小于孩子)
如图：请添加图片描述

所以我们另辟蹊径：先交换堆顶数据和最后一个数据这样中间的关系并没有造成混乱，然后数据个数减减，之后调整最后一个数据交换上去后的堆(只需要比较这个堆顶元素和孩子的关系达到满足关系) — 先比较它的两个孩子(左孩子和右孩子)大小关系，找到小的一方再和堆顶数据比较若小其则交换依次往后比较交换直到孩子的下标>=数据个数就停止。
注意一点：可能它只有左孩子没有右孩子，所以我们要对右孩子判断一下右孩子下标要小于堆数据个数才行不然就越界了

💫3.5.1 堆向下调整算法：

现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

📝3.5.1.1 代码(以小堆为例)：

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;//假设左孩子小
	while (child<n)
	{
		if (child+1<n&&a[child + 1] < a[child])
		//child+1<n判断右孩子下标满足不越界再比较
		//a[child + 1] < a[child]右孩子<左孩子,就代表右孩子小child++就是右孩子
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

📝3.5.1.2 流程图：

在这里插入图片描述

💫3.5.2 堆向下调整算法(删除)：

void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	//首尾交换
	Swap(&php->a[0], &php->a [php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

🌏3.6 堆的堆顶数据：

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}

🌏3.7 堆的堆数据个数：

int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

🌏3.8 判空：

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

🌏3.9 释放：

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

🌟四、堆实现的完整代码：

//Heap.h
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void HeapInit(HP* php);
void HeapDestroy(HP* php);
void HeapPush(HP* php, HPDataType x);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool HeapEmpty(HP* php);
int HeapSize(HP* php);

//Heap.c
#include"Heap.h"
void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = 0;
	php->capacity = 0;
}

void HeapDestroy(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}

void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	if (php->size == php->capacity)
	{
		int newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	AdjustUp(php->a, php->size);
	php->size++;
}

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child<n)
	{
		if (child+1<n&&a[child + 1] < a[child])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

//删除堆顶数据
void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	//首尾交换
	Swap(&php->a[0], &php->a [php->size - 1]);
	php->size--;
	AdjustDown(php->a, php->size, 0);
}

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

//Test.c
#include"Heap.h"
void HPTest()
{
	HP hp;
	HeapInit(&hp);
	int a[] = { 65,100,70,32,50,60 };
	for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
	{
		HeapPush(&hp, a[i]);
	}

	while (!HeapEmpty(&hp))
	{
		int top = HeapTop(&hp);
		printf("%d\n", top);
		HeapPop(&hp);
	}
}
int main()
{
	HPTest();
	return 0;
}

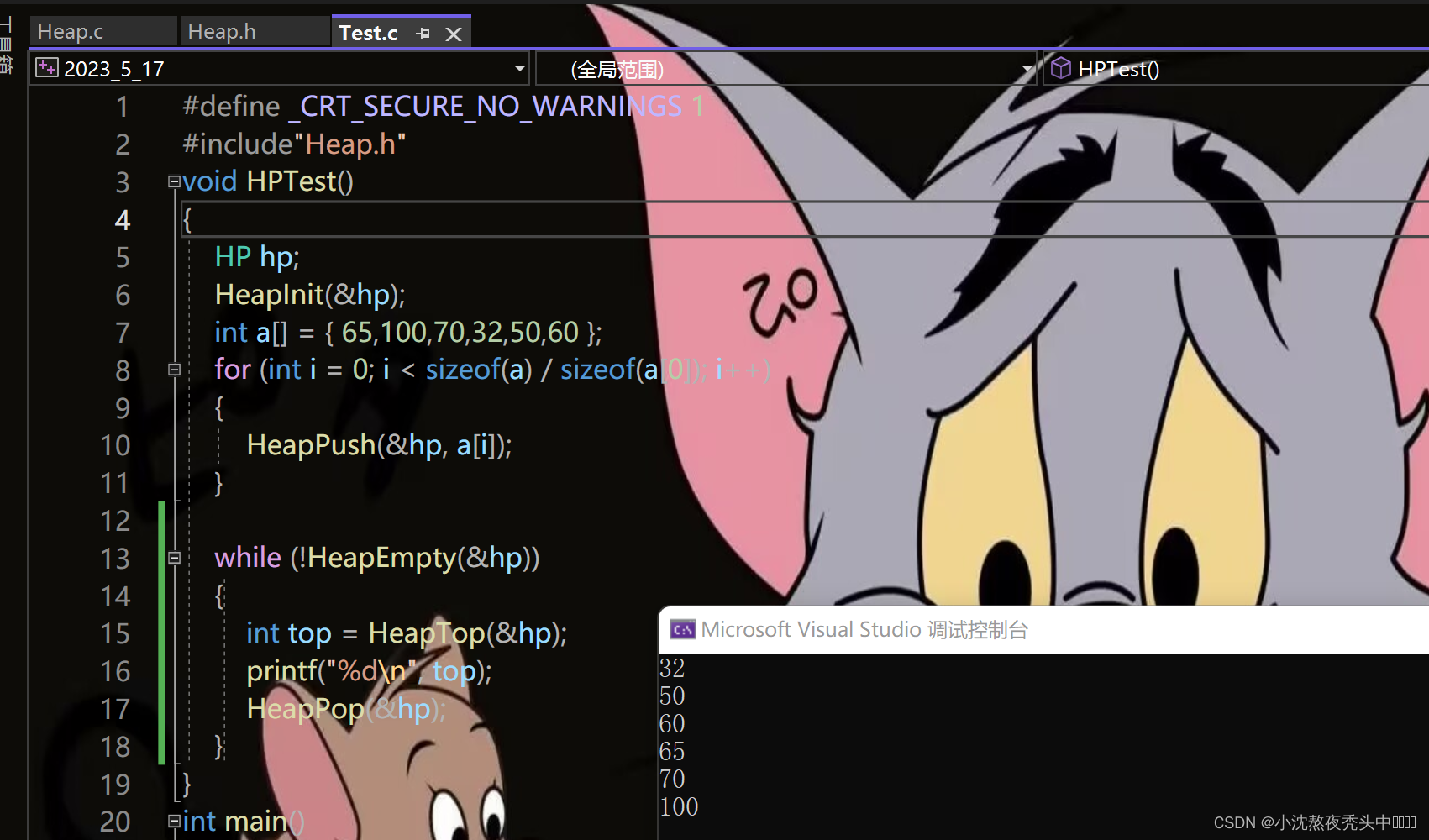
🌟五、堆伏笔：

对于上述代码实现后，运行会发现以小堆为例我们完成的堆是一个有序的顺序，这就为下一章对于堆的应用做了一个铺垫
请添加图片描述

😽总结

请添加图片描述
😽Ending,今天的二叉树 — 堆的概念+结构+代码实现 的内容就到此结束啦~，如果后续想了解更多，就请关注我吧，一键三连哦 ~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/552345.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Spring Security 如何实现身份认证和授权？

Spring Security 如何实现身份认证和授权？

Spring Security 是一个开源的安全框架&#xff0c;提供了基于权限的访问控制、身份认证、安全性事件发布等功能。在 Spring Boot 应用中使用 Spring Security 可以非常方便地实现用户身份认证和授权。 Spring Security 实现身份认证的主要方式是使用认证过滤器链&#xff0c;…
阅读更多...
C语言入门级小游戏——扫雷

C语言入门级小游戏——扫雷

文章目录 游戏思路游戏文件的创建游戏菜单棋盘的创建初始化棋盘打印棋盘 布置雷排查雷game.h —— 游戏函数的声明game.c —— 游戏函数的实现test.c —— 游戏的测试 今天我们写一个小游戏——扫雷来增加我们对编程的兴趣 希望这篇文章对友友们有帮助! 游戏思路 游戏文件的创…
阅读更多...
Linux：iptables防火墙(SNAT和DNAT）

Linux：iptables防火墙(SNAT和DNAT）

Linux&#xff1a;iptables防火墙 一、SNAT策略及应用1.1 SNAT原理1.2 SNAT应用 二、DNAT策略及应用2.1 DNAT原理2.2 DNAT应用 一、SNAT策略及应用 1.1 SNAT原理 SNAT 应用环境&#xff1a;局域网主机共享单个公网IP地址接入Internet&#xff08;私有不能在Internet中正常路由…
阅读更多...
MySQL数据库笔记——进阶篇

MySQL数据库笔记——进阶篇

文章目录 存储引擎MySQL体系结构存储引擎简介InnoDB介绍MyISAMMemory 存储引擎的选择小结 索引概述索引结构概述BtreeBTreeHash 存储引擎 MySQL体系结构 连接层&#xff1a; 最上层是一些客户端和链接服务&#xff0c;主要完成一些类似于连接处理、授权认证、及相关的安全方案…
阅读更多...
《计算机网络—自顶向下方法》 Wireshark实验（十）：NAT 协议分析

《计算机网络—自顶向下方法》 Wireshark实验（十）：NAT 协议分析

NAT&#xff08;Network Address Translation&#xff09;网络地址转换&#xff0c;即在私有地址和全局地址之间转换的协议。私有地址是不能用在 Internet 上(路由器将丢弃寻址这种地址的包)的内部地址。这些地址是不能够在公网上面用的&#xff0c;只能用在局域网的内部。私有…
阅读更多...
win安装Nodejs

win安装Nodejs

文章目录 1、安装环境2、安装步骤3、更换npm源为淘宝镜像4、更多node版本下载 1、安装环境 node.js下载官网: nodejs官网 点击选中图标下载即可&#xff1a; 2、安装步骤 1、双击安装包&#xff0c;一直点击next 2、点击change按钮&#xff0c;更换到自己的指定安装位置&…
阅读更多...
基于fpga的图像处理之3x3_5x5算子模板中值排序

基于fpga的图像处理之3x3_5x5算子模板中值排序

本文的思路框架&#xff1a; ①本文介绍3x3算子模块和5x5算子模块中&#xff0c;矩阵转化成串行数据后&#xff0c;对其排序&#xff0c;并获取矩阵中值数据&#xff1b; ②本例程中采用的FPGA设计技巧&#xff0c;可用于借鉴&#xff0c;一是采用for循环实现串行数据转化并行数…
阅读更多...
vite创建vue2项目

vite创建vue2项目

使用vite首先需要注意官方给出的兼容性注意 Vite 需要 Node.js 版本 14.18&#xff0c;16。然而&#xff0c;有些模板需要依赖更高的 Node 版本才能正常运行&#xff0c;当你的包管理器发出警告时&#xff0c;请注意升级你的 Node 版本。 1.初始化vite项目 输入以下命令&#…
阅读更多...
Spring MVC 是什么？与 Struts 的区别是什么？

Spring MVC 是什么？与 Struts 的区别是什么？

Spring MVC是Spring框架中的一个模块&#xff0c;它提供了一种基于MVC&#xff08;Model-View-Controller&#xff09;架构的Web开发方式。与传统的JSP/Servlet开发方式相比&#xff0c;Spring MVC更加灵活、高效&#xff0c;可以帮助开发人员快速构建高质量的Web应用程序。本文…
阅读更多...
vue diff算法与虚拟dom知识整理(10) 梳理patch处理相同节点比较的基本逻辑

vue diff算法与虚拟dom知识整理(10) 梳理patch处理相同节点比较的基本逻辑

这次 我们来讲 diff算法处理到 当新旧节点 是同一个节点时的处理 我们之前也说过 如果不是同一个节点 他就会暴力拆旧 把新的插上去 但当他们是同一个节点 需要精细化比较 最做小化更新 这块我们还没有处理 打开我们的案例 打开 patch.js 对应其实就还是这一块还没有写 我们…
阅读更多...
PostgreSQL查询引擎——transform expressions之AEXPR_OP

PostgreSQL查询引擎——transform expressions之AEXPR_OP

static Node *transformAExprOp(ParseState *pstate, A_Expr *a){Node *lexpr a->lexpr; Node *rexpr a->rexpr; // 操作符左右表达式Node *result;/* Special-case "foo NULL" and "NULL foo" for compatibility with standards-broke…
阅读更多...
Bug——后端返回LocalDateTime类型数据中间出现一个T

Bug——后端返回LocalDateTime类型数据中间出现一个T

错误如下图所示: 返回的JSON格式数据里面会有一个多出来的T. 解决方案&#xff1a; 在后端的POJO层的实体类的LocalDateTime属性上面加上一个注解 JsonFormat(pattern"yyyy-MM-dd HH:mm:ss") 如下所示&#xff0c;然后在返回JSON格式数据时就不会出现那个多余的T了…
阅读更多...
C++之模板初阶

C++之模板初阶

目录 前言 1.泛型编程 2.模板 2.1 函数模板 2.1.1 函数模板概念 2.1.2 函数模板格式 2.1.3 函数模板的原理 2.1.4 函数模板的实例化 2.1.5 模板参数的匹配原则 2.2 类模板 2.2.1 类模板定义模式 2.2.2 类模板的实例化 前言 我们会不会有疑惑为什么C语言中&#xf…
阅读更多...
Python学习笔记——cmeans模糊聚类例程

Python学习笔记——cmeans模糊聚类例程

文章目录 模糊聚类应用简介安装环境demo&#xff1a;运行结果 模糊聚类应用简介 模糊聚类即通过模糊数学&#xff08;处理模糊或不确定性信息的数学方法&#xff09;的相关算法进行聚类分析任务。 常用的模糊聚类算法包括模糊C均值聚类&#xff08;FCM&#xff0c;Fuzzy-c mea…
阅读更多...
TryHackMe-Red Team Capstone Challenge (红队挑战）【真实红队模拟】

TryHackMe-Red Team Capstone Challenge (红队挑战）【真实红队模拟】

Red Team Capstone Challenge 注意&#xff1a;我不会在这里提及相关的flag&#xff0c;只专心打&#xff1b;flag可以自己用各个hostname尝试一遍 挑战作者的一句话 这个房间被评为坚硬&#xff0c;但因为它是你前面的一座山&#xff0c;它可能被评为疯狂。但是&#xff0c;…
阅读更多...
【Vue3】滑动验证组件 | 滑动验证

【Vue3】滑动验证组件 | 滑动验证

前言 滑块验证不只判断是否滑动到尾部&#xff0c;真正的目的是检测用户行为&#xff0c;检测行为是人为、脚本、还是其它。 防止使用脚本大量注册、请求等 。比如发送请求时&#xff0c;判断用户在某个页面停留了多长时间。登录、注册时是否点击了登录、注册按钮&#xff0c;…
阅读更多...
Lesson1——数据结构前言

Lesson1——数据结构前言

前言&#xff1a; 今天我们正式开始一个新的专栏——初阶数据结构&#xff08;C语言实现&#xff09;&#xff0c;本专栏后续持续更新时间复杂度空间复杂度、顺序表、链表、栈和队列、二叉树、排序等算法的相关知识&#xff0c;欢迎大家互相学习&#xff0c;可以私信互相讨论哦…
阅读更多...
一次oracle环境 enq: TX - allocate ITL entry锁问题分析

一次oracle环境 enq: TX - allocate ITL entry锁问题分析

enq: TX - allocate ITL entry锁问题分析 通过分析问题时间段两个节点的AWR报告&#xff0c;TOP1等待为锁竞争enq: TX - allocate ITL entry&#xff0c;该等待事件是由于缺省情况下创建的表的INITRANS参数为1,索引的INITRANS参数值为2.当有太多的并发DML操作的数据行处于相同的…
阅读更多...
日志模块封封装:单例模式+策略模式+构建者模式+bugly

日志模块封封装:单例模式+策略模式+构建者模式+bugly

日志模块封封装:单例模式策略模式构建者模式bugly 一.单例模式策略模式构建者模式二.日志模块封装1.日志等级&#xff1a;LoggerLevel枚举类2.日志输出类型&#xff1a;LoggerType枚举类3.ILogger接口4.LogCatLogger/FileLogger/NetWorkLogger/EmailLogger5.使用构建者模式创建…
阅读更多...
相同格式相同分辨率图片不同大小分析

相同格式相同分辨率图片不同大小分析

1、问题 有三张图片&#xff0c;如下&#xff1a; 这三张图片均为jpg格式&#xff0c;分辨率均为1851*580&#xff0c;肉眼看不出区别。但是大小不同。 2号为217KB&#xff0c;4号为1.15MB&#xff0c;5号为1.06MB。 我们看下常规信息&#xff0c;先看2号&#xff1a; 可以…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023