目录

1.什么是堆

堆的定义

结构体定义与函数接口

堆的初始化

堆的销毁

入堆

向上调整算法

大堆

出堆

向下调整算法

返回堆顶元素

判空

堆的应用

---

1.什么是堆

知道以上的存储方法，对于完全二叉树，有一个叫做堆的结构，堆本质就是一个完全二叉树，

堆分两种：1.大堆    2.小堆

除了是完全二叉树，大堆需满足任何一个双亲都大于等于孩子，对于小堆，任何一个双亲都小于等于孩子。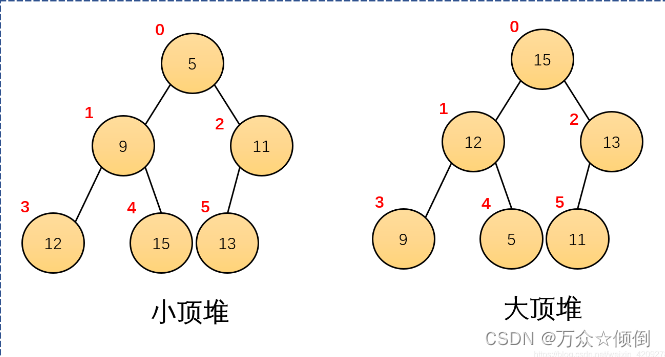

堆的定义

我们实现堆就用数组来实现的：这里以实现小堆为例

结构体定义与函数接口

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int HPDATAtype;
typedef struct Heap
{
	HPDATAtype *a;
	int size;
	int capacity;
}HP;

void Heapinit(HP* f);
void Heapdestroy(HP* f);
void Heappop(HP* f);
void Heappush(HP* f , HPDATAtype x);

堆的初始化

void Heapinit(HP* f)
{
	//初始有4个空间
	assert(f);
	f->a = NULL;
	f->size = 0;
	f->capacity = 0;
}

堆的销毁

void Heapdestroy(HP* f)
{
	assert(f->a);
	free(f->a);
	f->a = NULL;
}

入堆

void Heappush(HP* f, HPDATAtype x)
{
	assert(f);
	if (f->capacity == f->size)
	{
	int  newcapacity = f->capacity = 0 ? 4 : f->capacity*2;
      HPDATAtype* newnode = (HPDATAtype*)malloc(newcapacity);
	if (newnode == NULL)
	{
		perror("扩容失败\n");
		return;
	}
	f->a = newnode;
	f->capacity = f->capacity*2;
	}
	f->a[f->size] = x;
	f->size++;
	//向上调整算法
	Adjustup(f->a, f->size - 1);
	//向下调整算法
	//Adjustdown(f->a, f->size - 1);
}

在这里在入堆之后，也就是元素赋值到数组之后，根据你对数组的调整，也就是所说的向上调整算法，和向下调整算法，决定是小堆，还是大堆。

向上调整算法

我们这里通过对树所对应的数组元素的关系寻找父亲。 小堆：

void Adjustup(HPDATAtype*a, int child)
{
	//根据孩子zhaofuqin
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if ( a[child]<a[parent])
		{
		  HPDATAtype p = a[child];
		  a [child] = a[parent];
		  a[parent]=p;

		  child = parent;
		  parent = (child - 1) / 2;
		}
		else 
		{
			break;
		}
		
	}
}

大堆

这里只需要更改判断条件就变成大堆的调整

void Adjustdown(HPDATAtype* a, int child)
{
	//根据孩子找父亲
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			int tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp; 

        child = parent;
		parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
		

	}

}

出堆

出堆就是最后一个元素换到第一个元素，在size--，之后在进行调整。

void Heappop(HP* f){
	assert(f);
	//堆顶元素出堆,最后元素出堆
	assert(f->size);
	int tmp = f->a[0];
	f->a[0] = f->a[f->size - 1];
	f->a[f->size - 1] = tmp;
	f->size--;
	//向下调整
	Adjustdown(f->a, f->size, 0);
};

向下调整算法

出堆为了不改变原有的父节点与兄弟节点的关系，采用的是将堆底的最后一个与第一个互换，在减减，此时我们仍需要调整堆，采用向下调整算法---即从第一个节点处开始，找作为父节点的儿子节点中较小的那一个，两者比较，循环调整。

因此传参需要堆的大小以及第一个父亲结点坐标也就是0.

void Adjustdown(HPDATAtype* a, int size,int parent)
{
	int child =parent * 2 +1;
	while (child<size)
	{
		if ((child+1<size)&&a[child + 1] < a[child])//若右孩子存在且小于左孩子
		{
			++child;
		}
		if (a[child] < a[parent])
		{
			//交换
			int tmp = a[child];
			a[child] = a[parent];
			a[parent] = tmp;

			parent = child;
			child = parent * 2 + 1;
		}else
		{
			break;
		}
	}

}

返回堆顶元素

HPDATAtype HeapTop(HP* f)
{
	assert(f);
	assert(!HeapEmpty(f));

	return f->a[0];//返回堆顶数据
}

判空

bool HeapEmpty(HP* f)
{
	if (f->size == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

堆的应用

.堆可以用作优先级队列，实现高效的插入和删除操作

.堆可以用来解决海量数据的topk问题，即从大量数据中找出最大或最小的k个数

.堆可以用来进行堆排序，即每次把堆顶元素和堆尾元素交换，然后重新调整堆，直到堆为空

.堆还可以用来实现一些其他的算法，比如哈夫曼编码，Dijkstra算法等

需要注意的是对于向上排序算法还是向下排序算法，他们都是一对一对的使用，从而取决于你是大堆还是小堆，主要体现调整算法中的判断条件。