导读

磁共振(MR)图像诊断的准确性取决于图像的质量，而图像质量下降的主要原因是由于噪声和伪影。噪声是由成像环境错误或传输系统失真所引起的。因此，去噪方法对提高图像质量起着重要作用。然而，在去噪和保留结构细节之间需要权衡。现有的大多数研究都是针对特定的MRI模态或有限的去噪方案进行的。在此背景下，对不同的MRI去噪技术进行全面回顾是有必要的。本文为MRI去噪技术的分类提供了一个新的方向，包括近年来基于深度学习(DL)去噪方法的改进，以及传统的MRI去噪方法。本文还讨论了存在的主要挑战及其改进范围。此外，针对不同的数据类型，列出了相应的评估指标，从而帮助该领域的研究人员进行进一步的研究。

前言

MRI是一种可靠的临床影像诊断方法。成像方式的灵活性提供了更好的结构特征。MRI促进了具有相同分辨率的切片图像的多模态投影视图。MR图像处理的基本步骤包括增强、配准、分割、目标识别等。每个步骤都有许多分析方法。增强的一个重要步骤是去噪。低信噪比和高信噪比的MR图像分别用瑞利pdf和高斯pdf进行表征(pdf：分布概率密度函数)。此外，复杂MR图像中的噪声用加性高斯白噪声表示。MR图像中的噪声增加了识别特征的诊断过程的复杂性。在噪声传输系统中，由于成像环境或处理的错误而引入噪声。在模糊区域、无规则变化、边缘伪影可以看到噪声带来的影响。因此，消除噪声、保留边缘而不引入伪影是任何去噪过程的基本要求。目前有许多常用的图像去噪方法，也可以用于MR图像去噪。例如，均值、中值、维纳、扩散、基于域和范围的滤波器、空间域和变换域。广义上，可以将MR图像去噪的方法分为两种：①硬件方法；②软件方法。

第一种方法是通过改进MR扫描器的性能来消除噪声的。第二种方法是在记录数据的基础上，用合适的基于后采集方案的软件对图像进行去噪。为了系统地表示MR图像去噪的各种方法，可参见如图1所示的树形结构。方法分为空间域和变换域。在变换域，根据基函数的选择，将方法分为数据自适应技术和非数据自适应技术。数据自适应技术采用独立成分分析(ICA)来消除噪声。将非数据自适应技术进一步划分为频域和时间尺度(小波)域。

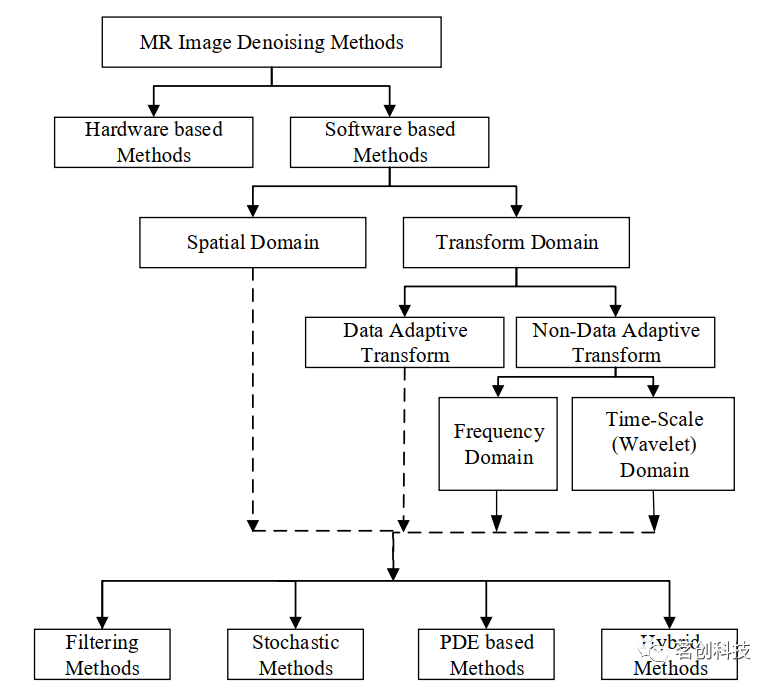
图1.MR图像去噪方法的分类。

接下来，进一步分类为滤波方法、随机方法、基于偏微分方程(PDE)的方法和混合方法，可以在空间域或变换域实现。虽然，这里对不同的方法进行了分类，但需要注意的是，它们并不是完全不同的，有些方法可能具有相互关系。

MR图像去噪技术

（1）数据自适应变换

基于数据自适应变换的方法采用ICA算法来消除噪声。该算法用于揭示统计独立因素和进行盲源分离。ICA是一种用于去噪多维MR数据的计算方法。这是一种用于计算机视觉系统建模的自适应高阶统计工具。McKeown等人(2003)提出了基于ICA的MR图像去噪技术。该方法是去除随机噪声，消除脉动和呼吸伪影的有效工具。Sukhatme和Shukla(2012)提出ICA作为一种具有特征值分解和降维的预处理方法。该方法最大化了互信息，同时最小化了MR图像中的非高斯噪声。Pignat等人(2013)在小波变换图像中使用ICA技术来提高去噪性能。该方法将空间图像分解为相应的小波系数。然后，采用ICA算法去除高斯噪声。该方法对图像的边缘增强也很有效。然而，这些方法都存在去噪性能和计算复杂度方面的局限性，这可以结合适当的优化算法来改进。

（2）非数据自适应变换

这些方法可以用频率变换、小波变换(WT)来表示。在该领域中，噪声消除和结构保存是同时实现的。

①频域

利用傅里叶变换(FT)实现了MR图像的频域表征。McVeigh等人(1985)提出了基于FT的滤波去噪MR图像。该方法利用功率谱估计噪声和测量标准差。Luo等人(2009)提出了一种基于奇异函数的MR图像去噪重建方法。在该方法中，首先将图像分成若干个频谱单元。然后，利用2D奇异函数分析对每个频谱单元进行去噪。通过平均重建得到去噪后的图像。Mustafi和Ghorai(2013)提出了基于分数阶傅里叶变换的医学图像去噪技术。该方法具有较好的去噪特性，适用于高敏感边缘图像的去噪，而且对盲源分离也很有用。未来，可以利用分数阶傅里叶变换的多态性质来提高去噪性能和边缘灵敏度。

②时间尺度(小波)域

目前已发表了多种基于时间尺度(小波)的MR图像去噪方法。这种变换将MR图像分解为小波系数的细节子图。绝对幅值小的系数通常是图像边缘的噪声或小结构。去除这些值可以减少重构图像中的噪声和细节。而准确阈值的选择在保留细节的同时，提高了去噪性能。Xu等人(1994)提出了一种用于MR图像去噪的WT域空间相关噪声过滤技术。空间相关性较高的区域与几个相邻的标度系数相关。Nowak(1999)提出了一种基于小波变换的MR图像中Rician分布噪声的去除方法。Zaroubi和Goelman(2000)提出了一种用于MR图像去噪的复杂去噪方案。该方法是利用软阈值来对小波系数进行阈值收缩处理。通过将图像分解为两组正交小波系数来进行去噪。Bao和Zhang(2003)提出用Canny边缘检测器对小波系数进行多尺度阈值去噪。Wink和Roerdink(2004)提出了基于小波变换的功能性MR图像去噪技术。该方法在2D小波系数中采用1D WaveLab阈值处理。

Wu等人()提出了基于小波变换去除MR图像中Rayleigh分布的技术。小波系数用非平稳数据表示。通过变换小波系数来分离不相关的噪声背景。Pizurica等人(2003)提出了AWT方法去噪MR图像。该方法能适应MR图像中噪声数据和信噪比的变化。利用分辨率尺度之间的相关性估计噪声小波系数。Anand等人(2010)提出了在小波域中使用双边滤波(BF)对MR图像进行去噪。该滤波方法在保留边缘特征的同时，能够有效地消除Rician噪声。Bartusek等人(2011)提出了一种基于优化小波变换(OWT)的MR图像去噪技术。该方法的目的是优化阈值水平和选择母小波。Luisier等人(2012)提出了用小波域的滤波器组来估计MR图像中的噪声作为非中心性可微卡方随机变量。

Habiba和Raghu(2017)提出在小波变换中使用对偶树复小波阈值函数去噪MR图像中的随机噪声。该方法可用于无穷维物体的去噪，如直线、曲线等。将对偶树复小波阈值函数和小波变换相结合，成功地平衡了平滑性和准确性。Agarwal等人(2017)对MR图像中带有随机噪声的不同小波方法进行了综合比较。Naveed等人(2019)建议对噪声MR图像的小波变换系数进行拟合优度检验。该方法在拟合优度检验背景下采用Anderson Darling统计量计算噪声小波系数。然而，利用局部噪声方差优化去噪性能可以作为该方法的未来发展方向。此外，小波变换还可以用其他一些旋转、平移和移不变的变换来代替。

小波变换不适用于高维边缘结构图像的分析。Wiek和Figiel(2014)提出用curvelet变换(CVT)去噪高维信息内容的大脑MR图像。利用多尺度几何理论对变换中的边缘信息进行表征。框架特征是用边缘的位置和缩放来表示的。受限CVT框架的稀疏表征便于傅里叶积分和拟微分算子。Bhadauria和Dewal(2013)提出了一种结合CVT和整体变分法去噪大脑MR图像的方法。利用CVT技术从残留噪声成分中提取MR图像中的结构细节。Vanitha等人(2016)提出用CVT来降低医学图像中的分数布朗运动噪声。实验采用BayesShrink、NeighShrink和VisuShrink等阈值化方法结合曲波变换对MR图像进行有效去噪。Biswas等人(2018)提出了一种基于维纳滤波器的CVT技术。该变换使用局部Ridgelet变换将图像分解为不相交缩放。基于CVT技术加上合适的阈值可以有效地消除MR图像中的Rician噪声。然而，未来可以寻找最优阈值来改进该方法的去噪性能。

Contourlet变换(CNT)是CVT的一种扩展，用于表示图像中的多维多分辨率特征。该变换采用拉普拉斯金字塔和定向滤波器组对特定频段的轮廓波进行分解。方向分解有利于图像中不同方向的分配和不同分辨率的缩放。Satheesh和Prasad(2011)提出了不同的阈值化方法与CNT来去噪MR图像。该方法采用不同的软硬阈值方法去除高斯噪声，并且提供了高定向各向异性纹理特征的有效表征。Kazmi等人(2012)提出基于阈值的CNT技术对大脑MR图像进行去噪。变换是通过两个连续的分解来完成的：多尺度和多方向。采用拉普拉斯金字塔进行多尺度分解，生成一组低通和带通图像。进一步利用定向滤波器组对每个带通图像进行多向分解，得到临界子样本。

（3）滤波方法

使用加权核来改进像素强度。噪声图像与加权核的卷积通过减少图像中的方差来降低噪声。所使用的内核可以是线性的，也可以是非线性的。因此，将滤波方法进一步分为线性滤波和非线性滤波，如图2所示。线性滤波使用平滑和时间滤波器来去除均匀分布的噪声。另一方面，非线性滤波器用于去噪非均匀分布的图像。在非线性滤波方法中，本文考虑了各向异性扩散(AD)，NLM，BF。

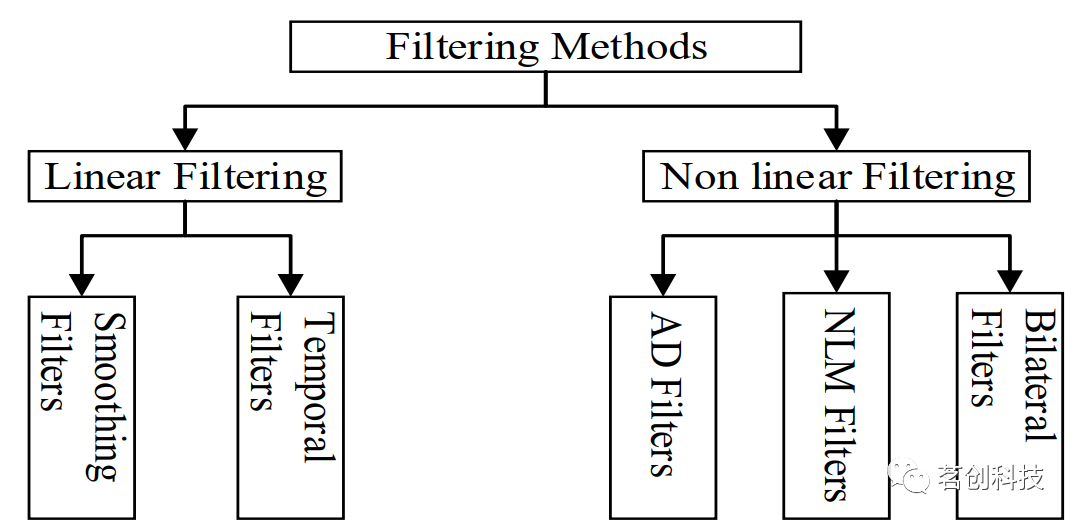
图2.滤波方法的分类示意图。

①线性滤波

平滑滤波方法使用平滑函数去噪图像中的高斯噪声(均匀分布噪声)。带有平滑核的噪声图像的卷积通过减少图像方差来减小高斯噪声效应。然而，由于滤波核中使用了参数相关的权重因子，图像中的精细细节是模糊的。这些技术用于降低图像中升高的空间频率。一般来说，平滑滤波是通过使用均值、中值、维纳滤波器及其改进来实现的。McVeigh等人(1985)提出用维纳滤波器(WF)来降低MR图像中的高斯噪声。他们假设噪声图像包含较高的空间频率值。使用这种滤波器的去噪技术提高了信噪比值。然而，由于模糊效应，图像边缘的特征细节被消除，从而降低了MR图像的清晰度。

Coupe等人(2013)采用一种自适应中值绝对偏差估计方法来去噪Rician噪声。Mohan等人(2015)利用定向窗口的中值滤波器(MF)的扩展，用空间结构特征从最大和最小中值进行边缘保存。Bin-Habtoor等人(2016)提出了均值和自适应中值滤波(AMF)来去除斑点噪声。Kadam和Borse(2017)提出了一种用于MR图像去噪的空间自适应滤波。然而，该技术的去噪性能仅限于椒盐噪声(又称冲击噪声或脉冲噪声)。Ali(2018)提出了自适应中值和WF来消除MR图像中的加性高斯噪声。Seetha和Raja(2016)比较了不同的基于滤波的MR图像去噪方法。定量分析表明，自适应维纳滤波器在消除加性高斯噪声方面优于自适应维纳滤波器。由于消除了小特征，所有平滑滤波器的性能都受到了限制。然而，使用边缘保留工具可以提高去噪性能。

时域滤波器用于消除图像中的时间变化。通过对采样间隔进行滤波，减少了图像序列中的快速变化、自旋回波效应和物体运动等时间变化。此外，为了消除混叠噪声，还直观地选择了采样间隔。McVeigh等人建议对不同采样间隔的MR图像进行时域滤波。滤波器消除了图像中的窄频分量。这会在更宽的频率引入混叠噪声，从而产生平滑的图像。然而，信噪比不受影响，因为噪声和信号都减少了相同的因素。通过将该滤波器与参数随机方法相结合，可以提高其去噪性能。

②非线性滤波

AD滤波器使用均匀区域的扩散，同时防止边缘的扩散。它不需要去噪过程之前的图像细节。这些标准使得该滤波器在非线性滤波器中很受欢迎。这些滤波器克服了在去噪和保持物体边缘时使用平滑滤波器的困难。AD滤波器是对来自邻近像素的局部信息进行选择性扩散。该滤波器基于二阶偏微分方程(2PDE)。Gerig等人(1992)提出了一种非线性AD滤波方法，用于去噪二维双回波自旋和三维梯度回波MR图像。该方法通过保留对象的详细信息，使信息损失最小化。然而，该模型具有分段持续和逐渐变化的特点，形成了具有稳定强度斜率的锋利边缘。

Murase等人(2001)提出对动态敏感MR图像进行扩散滤波以消除Rician噪声。Samsonov和Johnson(2002)提出了一种噪声自适应AD滤波方法来消除MR图像中的Rician噪声。该方法提取T2-w MR图像边缘的信息内容，而且根据不同的结构平滑MR图像的内部区域，得到的图像是一个多尺度的平滑图像，保留了细微的细节。此外，该研究者还提出了一种针对MR图像中空间变化的噪声水平的非线性AD滤波方法，用空间噪声分布因子来消除空间变化的噪声水平。Krissian和Aja-Fernandez(2009)使用噪声驱动AD(NDAD)滤波器来去噪MR图像中的Rician噪声。该滤波器依赖于MR图像噪声的标准差和偏微分方程的估计。根据图像的结构特性，建立了相干扩散矩阵。实验结果表明，该滤波器在保留边缘信息量的前提下，提高了收敛速度。Pal等人(2017)提出了一种基于矩量的AD滤波器来消除MR图像中的Rician噪声，引入了扩散系数对AD滤波器进行重构。这是从Rician噪声的二阶矩计算出来的。Cappabianco等人(2019)提出了一种可操作的AD滤波器用于MR图像去噪，它是对标准AD滤波模型的修正，加入了扩散电导因子。该过程中使用的边缘停止函数保留了图像边缘的结构细节，而扩散电导因子使其适合于噪声估计和对比度增强。该滤波方法可用于处理多通道扩散张量MR图像。

从文献中可以观察到，局部滤波的使用保留了大尺度的结构，但消除了细节。为了克服这一问题，利用图像中的冗余信息进行NLM滤波。这是通过将具有相似权重的图像的所有像素的均值合并到目标像素中来实现的。Manjon等人(2010)提出了基于NLM的不同滤波方法来消除MR图像中的Rician噪声。该研究者采用一种无偏NLM滤波方法，在保持结构可辨性的前提下，寻找磁矩MR图像去噪的最佳参数。他们采用基于区域的相似度比较，而不是像素相似度比较。这个过程使它独立于局部像素，去噪的鲁棒性更强。此外，作者还提出了一种基于自适应NLM滤波的方法，用于去噪具有空间波动噪声水平的MR图像。然后，提出了利用MR图像的稀疏性和自相似性的去噪技术。该技术基于余弦变换和三维旋转不变性的NLM滤波器的三维滑动窗口公式。然而，由于计算的复杂性，这类方法的性能受到了限制。Coupe等人(2006)提出了一种快速NLM (FNLM)方法，以减少MR图像去噪的计算时间。该研究者将其工作扩展到自动和优化的NLM (OBNLM)滤波方法中，用于去噪3D MR图像。这是通过并行计算模式中的block实现的。与传统的方法相比，该滤波器显著减少了执行时间。该研究者进一步采用基于小波阈值的OBNLM滤波对多分辨率MR图像进行去噪。然而，由于空间信息冗余，性能受到限制。Liu等人(2010)提出了一种基于高斯的非模拟NLM (UNLM)滤波方法来消除3D MR图像中的偏差。去噪是利用全局区域灰度的加权平均进行的。Hu等人(2012)提出了一种基于离散余弦变换(DCT)的NLM滤波去噪机制。该方法在DCT空间中计算相似性度量。该模型是为了消除噪声引起的畸变、改善计算复杂度而建立的。然而，大脑MR图像中相似的纹理可能具有不同的信息内容。Yu等人(2019)采用基于拉普拉斯特征映射网络的NLM滤波方法来降低MR图像中的噪声。它是通过计算特征提取的相似性来实现的。未来可以利用纹理特征和优化算法改进NLM滤波技术，以获得对混合噪声更好的去噪性能。

BF是一种基于几何和光度相似性来组合附近灰度的非线性方法。该滤波方法由Walker等人(2006)提出，用于平滑相邻像素非线性组合的图像。Mustafa和Kadah(2011)提出了多分辨率BF(MRBF)来近似小波域的子带分解和重构。利用小波阈值进行子带分解，使灰度平滑以消除高频噪声。Lin和Chang(2015)提出了一种参数优化技术，利用反向传播人工神经网络(ANN)来优化BF方法的性能。基于神经网络的参数优化利用了统计矩阵和灰度共生矩阵的特征。Phophalia和Mitra(2015)提出了基于粗集的BF(RSBF)来去除MR图像中的高斯噪声。该滤波器引入了空间贴近度的增益参数。该参数根据MR图像的粗糙类标签和边缘映射自适应。

用于识别图像中非均匀区域的BF的一种改进方法是三边滤波器。该方法在平滑图像时，除了几何和光度相似性外，还集成了局部结构相似性。该方法使用一个狭窄的空间窗口，只需要一次迭代来平滑图像。在多维信号上也进行了实验。该方法将像素值替换为邻域内几何相似性、光度相似性和局部结构相似性权重的均值。Chang等人(2011)提出了一种改进的TF来去除由于Rician噪声引起的波动。该滤波器使用基于极限压缩的秩序绝对差分统计量来消除MR图像中的Rician噪声。未来可以进一步优化滤波器参数的选择，以及该方法可以向随机噪声类型的自适应二维滤波方向改进。

（4）随机方法

这些方法本质上是随机的。这使得随机方法在噪声环境下处理MR图像更加合理。为建模各种估计量准备了一组初始条件和参数估计。该方法用于在去噪处理之前估计噪声特征及其方差特性。使用非线性函数，数据可以被建模为干净数据加上加性高斯或瑞利噪声的和。拉普拉斯概率密度函数可用于变换域内的干净数据。先验分布精确地表征了干净图像的重尾分布，利用了变换系数的尺度间特性。此外，利用局部信息估计模型参数，使去噪算法具有空间自适应能力。根据MR图像的噪声方差特征选择合适的模型。根据其总体估计标准，随机方法的分类如图3所示。

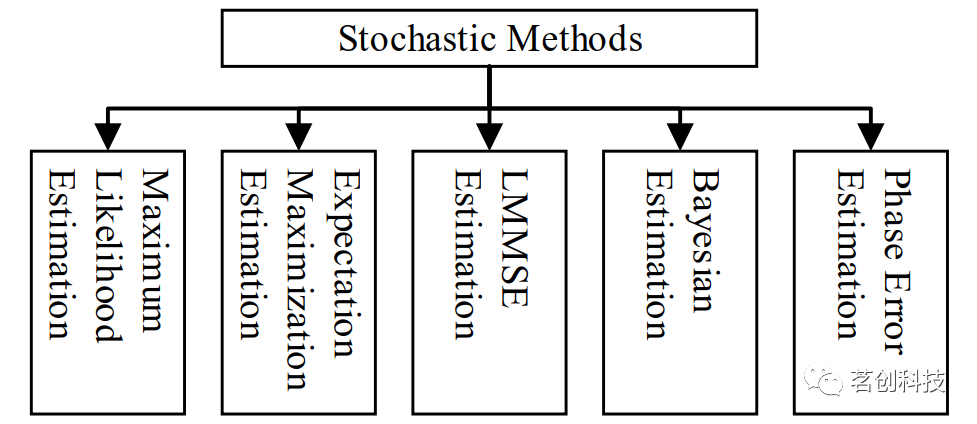
图3.随机方法的分类示意图。

①最大似然估计

最大似然估计是一种从有限高斯模型的概率分布计算参数的方法。这是参数空间中使似然函数最大化的值。Sijbers等人(1998)提出了使用ML估计去除Rician噪声和图像重建的不同方法。ML估计采用两级采集法获取噪声变化。该方法通过减去对同一目标的两次连续采集来计算噪声量。它减少了传统ML估计中出现的偏差效应。此外，Sijbers(2004)提出了用ML方法对复值MR数据进行参数估计。在这里，复杂MR图像中的高斯噪声分布使用其幅度分量重构为Rician分布。He和Greenshields(2008)建议对MR图像中的Rician噪声进行非局部ML(NLML)估计。该算法假设邻域相似的像素来自相同的分布。该方法利用非局部邻域像素中的ML估计量对潜在噪声进行预测。Rajan等人(2010)提出了不同的模型来估计无背景MR图像中的噪声水平。利用ML估计和局部偏度计算噪声方差。该方法为无背景MR图像去噪提供了一种有效的解决方案。该研究者后来提出了一种局部ML(LML)估计方法，用于去噪局部相邻像素受限的Rician分布MR图像；以及基于相似性的NLML估计用于去噪MR图像，并采用Kolmogorov-Smirnov方法计算灰度相似性。

②期望最大化估计

参数估计采用期望最大化(EM)法对存在潜在变量的高斯混合模型的ML进行估计。该方法计算潜在变量，并迭代优化模型。因此，在参数估计过程中避免了噪声方差的计算。Maitra和Faden(2009)建议在去噪幅度MR图像时使用EM技术进行参数初始化和方差估计。参数估计与噪声图像中背景像素的数量无关。Martin-Fernandez和Villullas(2015)提出了一种基于概率小波变换的MR图像去噪方法。该方法有助于合并两个高斯分布而不偏离实际分布。此外，通过迭代学习过程降低了计算复杂度。

③线性最小均方误差估计

线性最小均方误差估计(LMMSE)去噪MR图像是一种利用二次损失函数最小化均方误差的通用方法。结果表明，该方法对图像中存在依赖像素的区域是有效的。Aja-Fernandez等人(2008)建议使用LMMSE估计来最小化扩散加权MR图像中的Rician噪声。这些方法利用局部统计样本分布来计算图像中的噪声功率。每个像素的实际值是通过自适应LMMSE(ALMMSE)估计来计算的。此外，利用局部统计样本分布的动态噪声估计对噪声MR图像的去噪和特征保留是有效的。

Golshan等(2011)提出了一种信号依赖的偏置LMMSE估计方法，用于消除MR图像中的Rician噪声。该方法利用硬阈值计算控制参数的非局域LMMSE估计。此外，他们提出了一种改进的循环LMMSE(RLMMSE)估计用于去噪3D MR图像。该方法在假设一个随机场的前提下，结合非局部邻近空间信息对MR图像中的样本进行估计。通过考虑3D MR图像的冗余度，改进了模型的结构相似性度量。

④贝叶斯估计

这是一种在缺乏支持参数的情况下，从邻域估计像素真实值的随机方法。因此，该方法也被称为非参数估计技术。Awate和Whitaker(2005)提出了一种用于MR图像去噪的非参数估计方法。该方法将图像视为随机场，利用降低耦合的Rician噪声模型从有噪声的MR图像中计算高阶相干数据。使用非参数密度估计对MR图像进行贝叶斯去噪。此外，该研究者还提出了一种扩展的非参数经验贝叶斯方法，用于保留MR图像的特征和去噪。从含有Rician分布噪声的MR图像中计算去噪后的图像统计量。利用EM技术通过优化的数据指标估计该先验。经验贝叶斯方法为MR图像的去噪和特征保存提供了拟合方法。

⑤相位误差估计

相位误差估计是一种基于模型的迭代恢复过程，计算无散斑物体相位和反射率的最大后验概率(MAP)估计。利用一系列非线性滤波器对噪声图像进行相位估计。利用估计的相位误差重构每个数据点的相位校正。估计相位误差中的虚分量就是噪声图像中的噪声污染物。这很容易消除。该方法可以有效地保存MR图像中的边缘。Tisdall和Atkins(2005)提出了一种基于相位误差估计的低信噪比MR图像去噪方法。与其他非线性滤波方法(如AD、NLM滤波)相比，该方法具有更好的边缘保存效果。这是一种潜在的复值MR图像去噪方法，没有过度平滑的风险。

（5）基于PDE的方法

为了使图像强度的拉普拉斯函数绝对值最小，建议采用高阶PDE(HPDE)滤波器。得到的图像比使用2PDE获得的步进图像更自然。Lysaker等人(2003)使用基于平滑的四阶PDE滤波器来消除MR图像中由于阶梯效应而产生的伪影。该技术在空域和时域都进行了实验。在平滑变化的灰度值下，对块状效应具有较好的效果。Jin等人(2008)提出了一种改进的HPDE滤波，利用像素与其邻域的一致性去噪MR图像。像素相似性度量像素在其邻域内的归属性，从而减少噪声。Rajan等(2009)采用HPDE滤波中的非线性复扩散方法来消除MR图像中的噪声。非线性复扩散方法在保持边缘信息细节的同时，又能有效地降低噪声。Khanian等人(2014)提出了一种用于MR图像去噪的最优PDE滤波技术。该方法基于一种新的停止准则，利用区域内较高的频率相对差因子。Jansi和Subashini(2014)采用基于RudinOsher-Fatemi滤波器的PDE去除MR图像中的Rician噪声。该方法还通过不连续处理消除了边缘区域的斑点。Heydari和Karami(2015)提出了利用邻域像素相似性的改进扩散函数。Kollem等人(2019)提出了一种自适应的四阶PDE滤波器，用于去除MR图像中的Rician噪声。该滤波器通过使用梯度和拉普拉斯函数来缩短PDE的执行时间。考虑到整个图像是平面的，PDE方法试图在保留边缘区域的同时降低噪声。然而，这些技术可以进一步改进，在保留高噪声图像中的结构细节的同时，平滑高频分量。

（6）混合方法

除上述研究外，很少有研究报告使用混合方法进行去噪。Liu等人(2015)提出的混合方法是将模糊聚类和NLM滤波相结合，用于去噪大脑MR图像。Aravindan和Seshasayanan(2018)提出了将离散小波变换与MBO算法相结合的MR图像去噪方法。Rabbani等人(2009)提出了一种小波变换域的拉普拉斯混合模型来降低MR图像中的Rayleigh分布噪声。使用的统计模型有助于降低去噪过程中的失真。Ashamol等人(2008)提出了一种混合方法，将平稳小波变换(SWT)和CVT与AD滤波相结合，用于去噪MR图像中的高斯噪声。此外，Kala和Deepa(2019)结合空间域BF和优化的小波变换域阈值来去噪MR图像。第一阶段BF用于对分解图像的低频子带进行去噪；第二阶段BF对噪声图像中的高频分量进行去噪处理。表1总结了各种MR图像去噪方法的优缺点。

表1

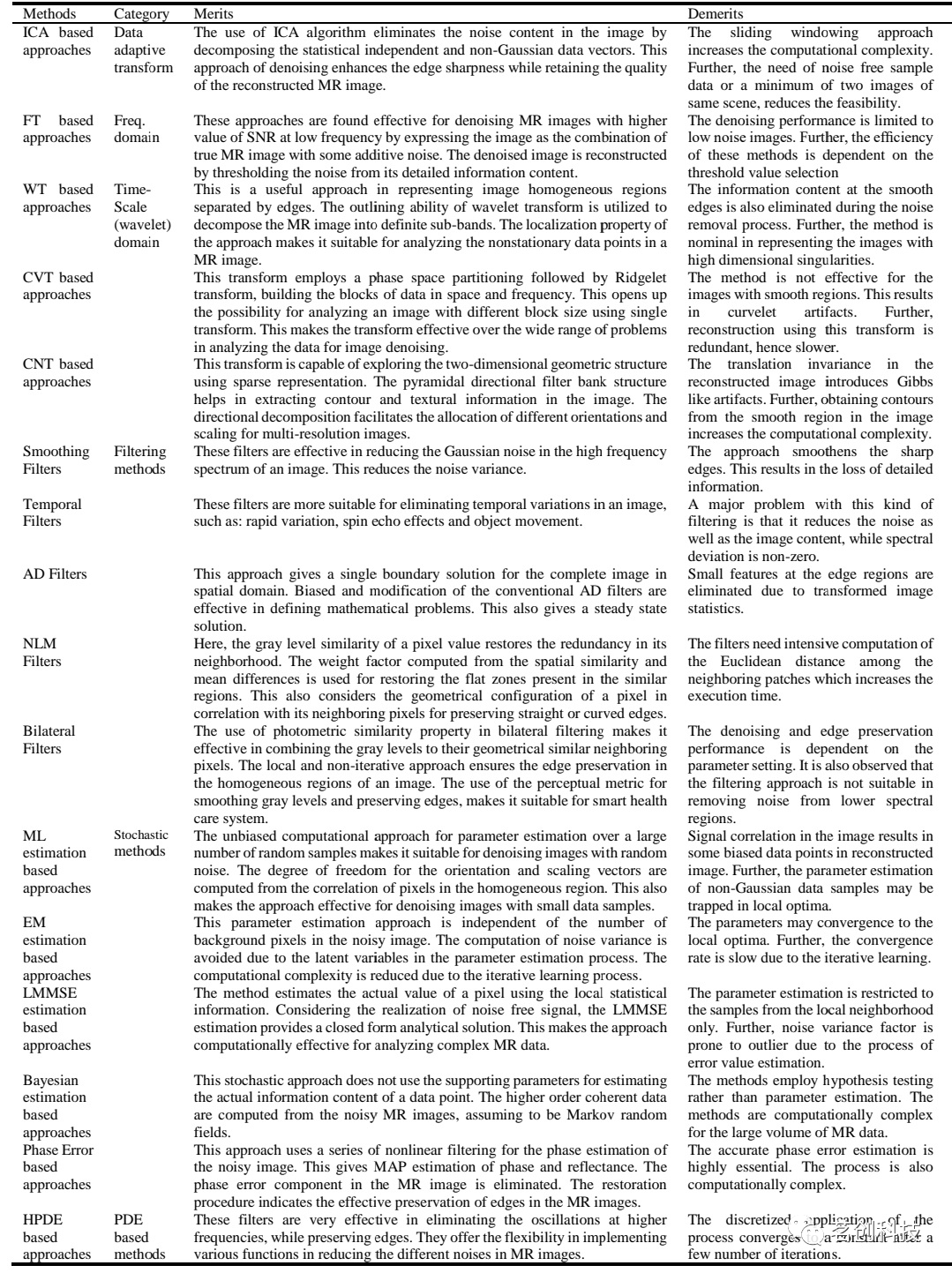
评估参数和数据库

评估参数。MR图像去噪是预处理的基本要求。文献中有大量的评估指标用于验证去噪技术。具体而言，信噪比、MSE、结构相似性(SSIM)、基于局部方差的质量指数(QILV)是最常用的评估指标。表2对许多评估指标作了简要说明。符号Xref表示参考图像，Xdno表示去噪后的图像。

表2

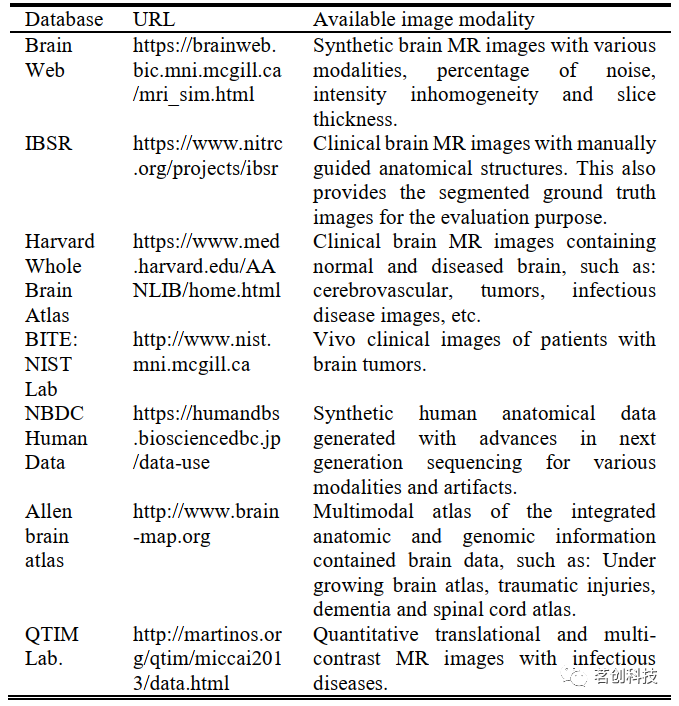
大脑MR图像数据库。表3提供了关于公开数据库及其URLs的简要信息。

表3.常用的大脑MR图像数据库。

结论

本文为MR图像去噪算法的分类提供了一个框架。总的来说，滤波方法对去除均匀区域的高斯噪声更为简单有效。该方法的潜在缺点是通过模糊非均匀区域来消除小结构和边缘细节。其次，小波变换域方法与随机方法相结合，能够有效地去噪和保留复杂MR图像的边缘细节。此外，将前两者与随机方法、优化工具或基于机器学习的方法相结合，可以获得更好的去噪性能。从这篇文章中，研究人员可以了解关于任何特定MR图像的最合适的去噪技术。

原文：A Survey on State-of-the-art Denoising Techniques for Brain Magnetic Resonance Images.

DOI: 10.1109/RBME.2021.3055556