简单介绍

HashMap是Java中最最常用的容器之一,在工作中肯定会用到, 但是很多人也没有仔细阅读过源码, 梳理过底层细节. 本篇文章就带大家一起从问题出发, 阅读源码, 从源码中寻找答案.

这个也是阅读源码的一个技巧, 提出一个问题, 自己先想一个实现流程, 然后从源码中进行验证, 这样就不会索然无味,晕头晕脑, 可以专注于其中一个流程脉络.

本篇文章主要基于JDK1.8版本进行分析.

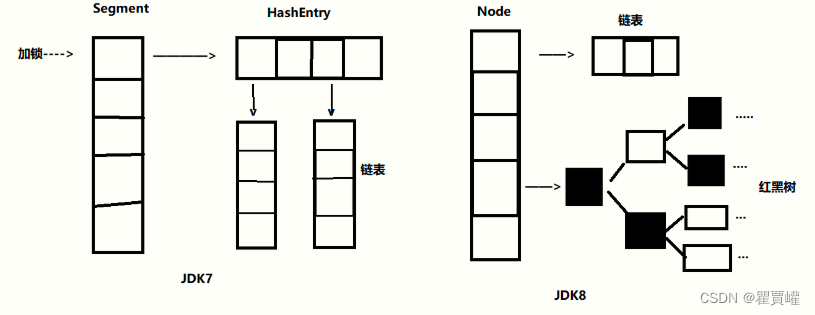
HashMap的底层结构大家都知道,是数组+链表结构,当链表长度>8时就会转为红黑树,因为链表查询复杂度为O(n),而红黑树的查询复杂度为O(logn),这样可以提高查询效率.

底层结构再深入一些,我们可以了解到,这个数组中其实存的是一个一个的Node,这个Node是实现于Entry的,也就是一个key,Value结构.

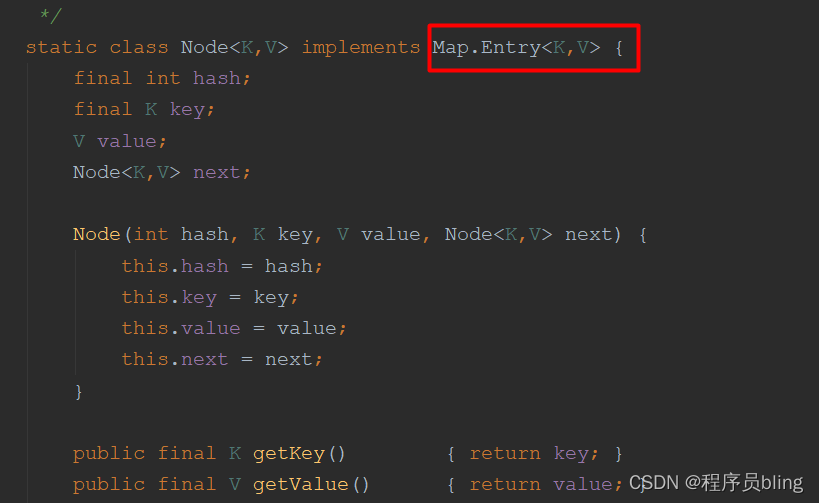
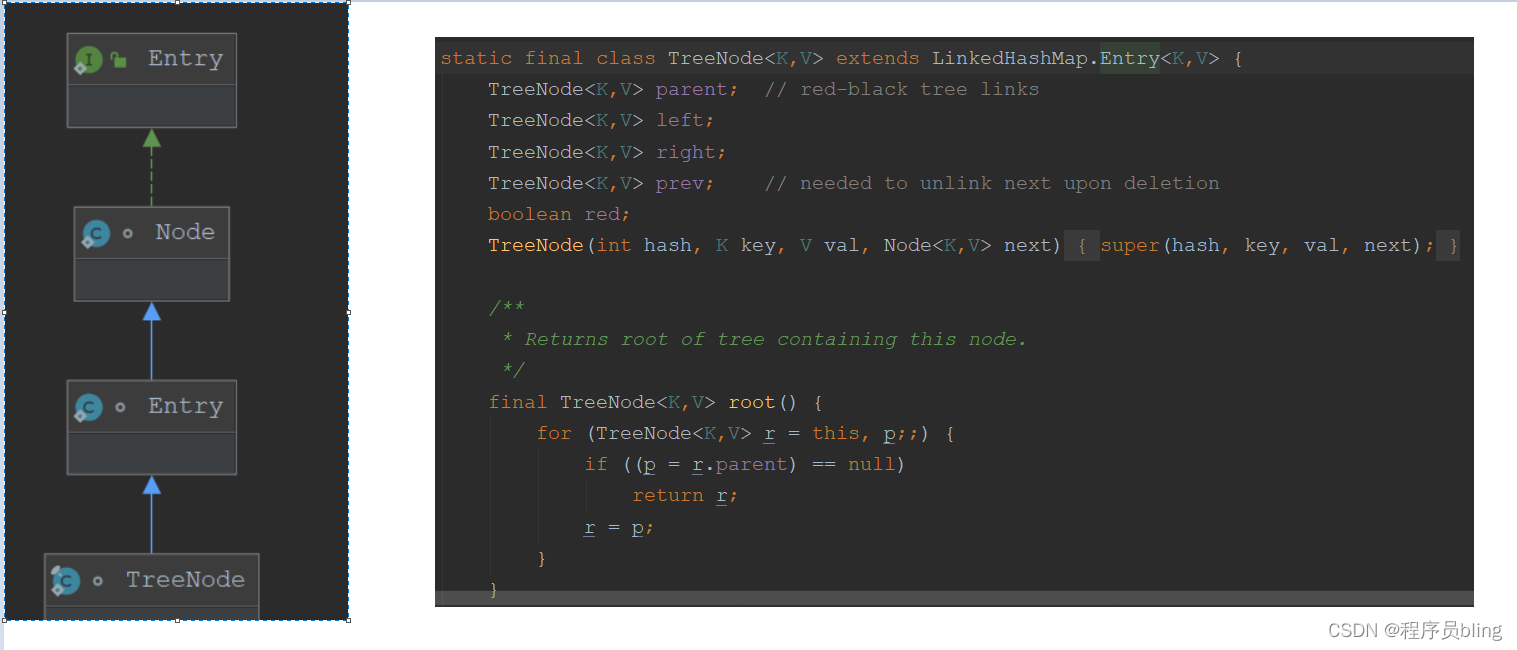
而在HashMap中, 其实还有个TreeNode结构, 当由链表转成红黑树时,也会进行结构的改变,将Node转成TreeNode.

这个TreeNode其实继承于Node类, 所以它也会有next属性.但是他还有一些额外的属性,比如说left, right, prev, 所以在HashMap中的红黑树其实不仅是一个红黑树,还是个双向链表,因为它有prev,next属性, 这个是为了操作方便,因为涉及到链表和红黑树结构的相互转换.

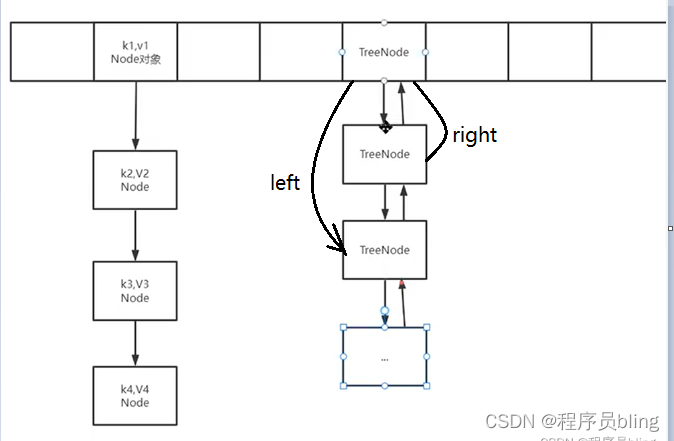
现在结合我们已有的一些基础知识, 就结合源码进行分析梳理了.

提出问题

首先提出一些问题, 尝试自己去解答, 以下是博主自己好奇的一些问题? 将在本文进行验证, 小伙伴如果有其他的问题,也可以在评论区提出, 博主也会进行解答.

1. put元素的流程?
2. 怎样找到要存储的下标位置的?
3. 什么时候会扩容? 加载因子、阈值这些有什么含义?
4. 怎样扩容的?扩容的流程?
5. 链表可以转成红黑树, 那会从红黑树转成链表吗?
6. 什么时候会从链表转成红黑树?

流程说明及验证

put元素的流程

先看这个问题的时候, 先理清大致脉络, 一定要不求甚解, 刚开始把握主体流程, 不要陷进去.

1. put元素入口.
   
2. put方法流程解释
   

综合以上我们可以得出put元素大致流程:

• 首先根据我们传入的key算出一个hash值,然后再通过一定的操作算出应该存储的下标
• 根据下标判断是否key相等,相等进行value的更新
• 不相等的话就有三种情况, 如果该位置没有值, 直接赋值, 还有就是在红黑树和链表上新增节点的操作
• 当整个map中存储的元素大于threshold(阈值)时,就会进行扩容.

怎样找到要存储的下标位置的?

从主体流程中我们能够知道计算下标的逻辑主要在这一行,其中n是数组的长度, hash就是key的hash值.

index=(n-1) & hash

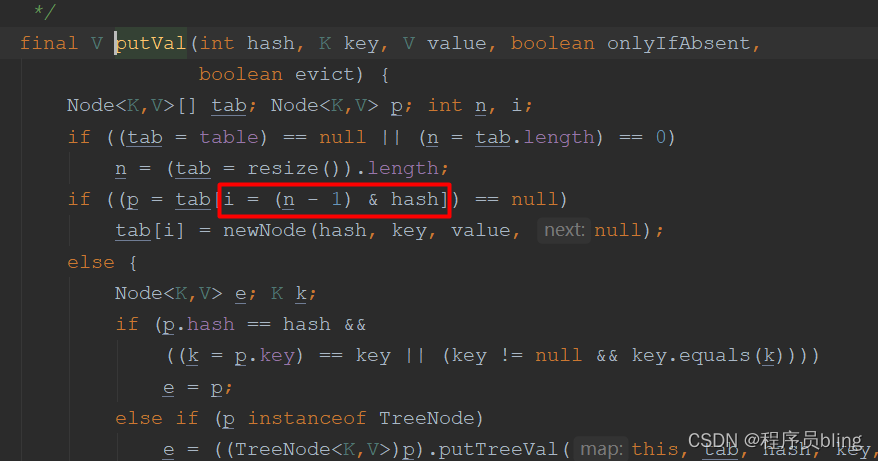
看到这里可能会有点蒙, 如果是我们自己处理的话,应该用hash值对数组长度取余, 这样就能够很方便找到对应的下标, 这里进行 & 运算能够达到这种效果吗? (&运算代表 两个数均为 1 结果才为 1 )

我们这里就带入实际情况试试, 数组的默认长度是16 ,n-1也就是15 , 15和key的hash值进行 & 运算. 这里我们hash值随便取一个.

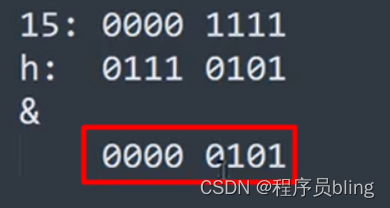
看到这里可能你就恍然大悟了, 因为15对应的二进制数是 0000 1111, 所以这里就可以取到0-15,从而找到对应的下标.

不过这里是有些取巧的, 只有一些固定的长度才可以, 而其他数, 比如说8-> 0000 1000 不论和任何数 & 运算, 都只会有两种结果, 达不到我们想要的效果.
所以在hashMap中,数组的长度一定是2的次方数,因为2的次方数一定是有一个位数是1,其他是0,这样-1之后才能进行位运算.

什么时候会扩容? 加载因子、阈值这些有什么含义?

当map中存储的元素个数 > 某一个阈值时会进行扩容, 也就是说阈值的大小控制着什么时候扩容.

那阈值是什么呢?
阈值=加载因子 * 数组大小

而这里的加载因子其实就是填充率,比如默认原数组大小是16,加载因子是0.75,那么就是已用数组的长度达到12就会进行扩容.

如果我们把加载因子调整到1,当map中存储元素大小达到16才会进行扩容.此时很可能就已经发生了很多的哈希冲突.

所以,加载因子越小，填满的数据就越少，哈希冲突的几率就减少了，但浪费了空间，而且还会提高扩容的触发几率；
加载因子越大，填满的数据就越多，空间利用率就高，但哈希冲突的几率就变大了。

这就必须在“哈希冲突”与“空间利用率”两者之间有所取舍，尽量保持平衡，所以这里取了一个适中值0.75.

怎样扩容的?扩容的流程.

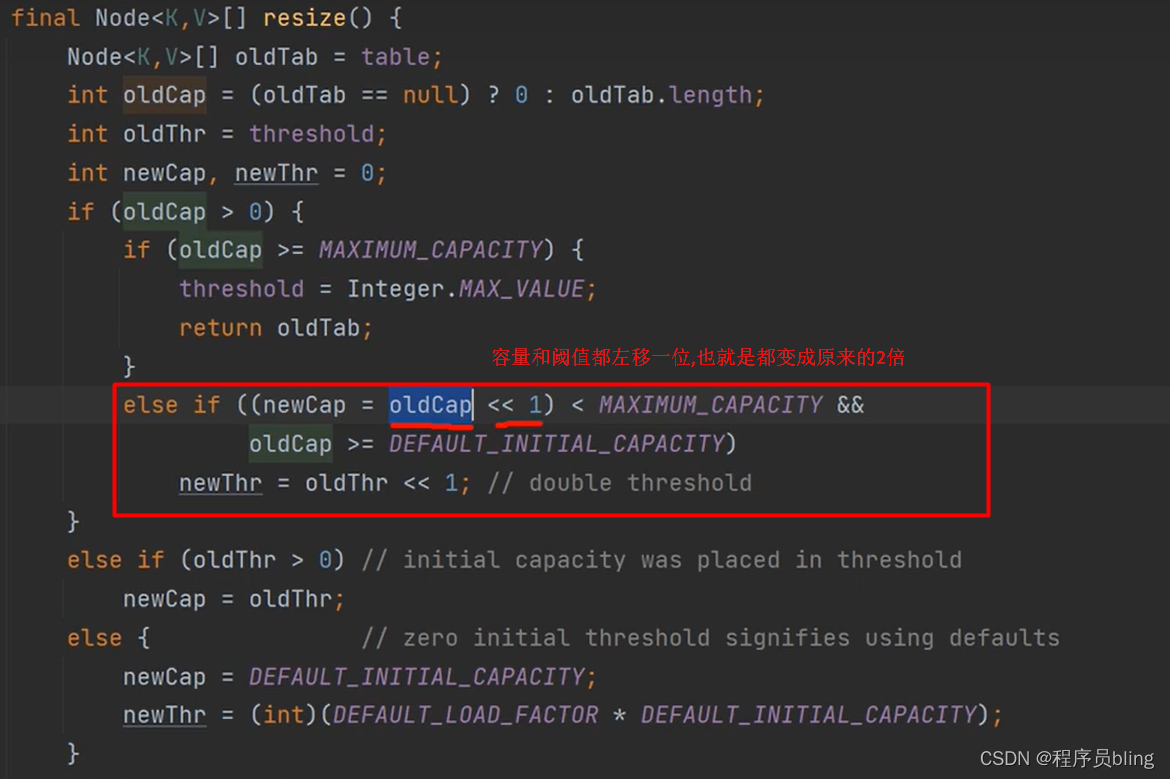
扩容方法都在resize()方法中,那会扩容多少呢? 我们先看一下resize()的前半部分,可知会扩容到原来的两倍.

那扩容要干什么? 我们先来自己思考一下这个过程.就拿从数组长度为16扩容到32 这个过程来说.

首先数组是不可变的,要扩展数组长度, 必须新建一个数组, 然后把原来数组中的数据 全部重新hash,重新计算下标值, 再移到新的数组中.

这个是我们自己直观能想到的,那真实是不是这样的呢? 需不需要全部重新计算下标值呢? 其实在源码里面没有这么做, 这里有一个很有意思的点.

这里其实有个规律,我们举个例子.还用最开始的计算hash值的方法.
index=(n-1) & hash
本来长度是16扩容到32.

这种情况下,新的下标刚好比原来的下标大了2的4次方.也就是16.

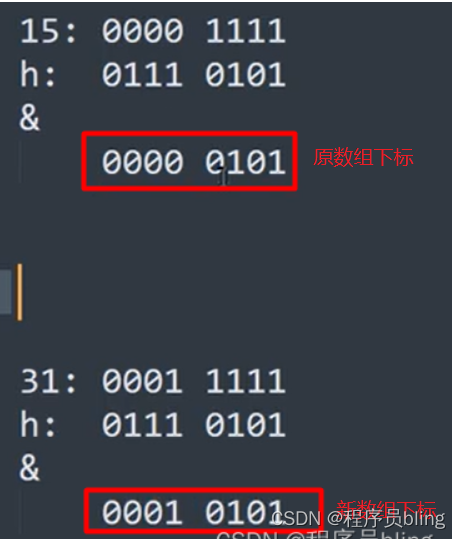
这种情况下,新下标位置和原下标位置相同.

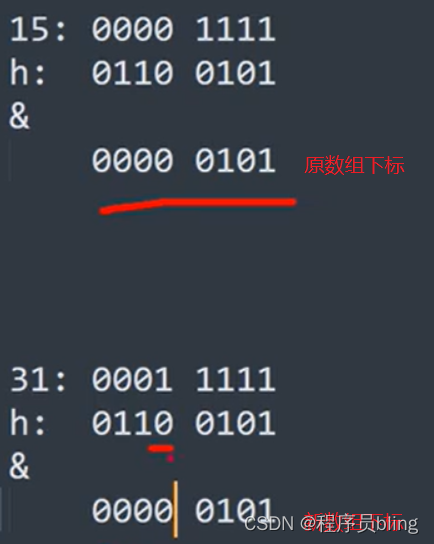
你会发现其实就只有这两种情况,

• 新下标比原下标大16,这个16刚好就是原数组的长度.
• 新下标和原下标位置一致.

因为二进制低四位都是一样的,就只有第五位不同.

也就是说第五位控制着新下标的位置,我们要判断这一位是0还是1,那怎样判断某一位是0还是1呢?

其实也比较简单, 就是和只有这个位置为1的数进行 & 操作即可. 而这个数也刚好就是原数组的长度—>16—> 0001 0000,即:

• key的hash值 & 原数组长度 == 1 时: 新下表=原下标+原数组长度
  key的hash值 & 原数组长度 == 0 时: 新下表=原下标

在源码中把这两种情况分为 高位 和 低位.

接下来一起看看源码:

链表可以转成红黑树, 那会从红黑树转成链表吗?

如果红黑树可以再转成链表,这个其实在哪方面最可能? 就是在扩容的时候.

在我们上面总结规律的时候,知道原数组的一个链表在扩容的时候,会拆成两个链表, 也就是分为高位和低位两拨, 那红黑树呢? 拆成两个红黑树? 这个其实不一定.

首先明确这个红黑树上的节点也会最终被拆分为两拨,高位和低位.

那红黑树其实还有一个点,就是在hashMap的设计原则中,链表长度>8时才应该是红黑树,所以一个红黑树拆分之后就不一定还是红黑树了,就可能变成链表.这个取决于拆分后的长度.

那具体红黑树是怎样转移到新数组的呢, 拆分过程如下 :

1. 先将红黑树拆分成两个链表
2. 根据两个链表的长度判断,需要的话将其转成红黑树
3. 将链表或者红黑树的头结点赋值给新数组

再看一下源码,也就是resize()方法中的split()方法.

扩容的时候可能将红黑树转成链表,那可能还有一种情况,就是删除元素后,红黑树中的长度小于9时,会不会退化成链表呢?

这里当长度小于9时,其实不会退化成链表,但是当满足根节点为null或根节点的右节点为null、或者根节点的左节点为null、或者根节点的左节点的左节点为null时,会退化成链表.此源码在remove( )—>removeTreeNode( ) 方法中,有兴趣的同学可以去看一下.

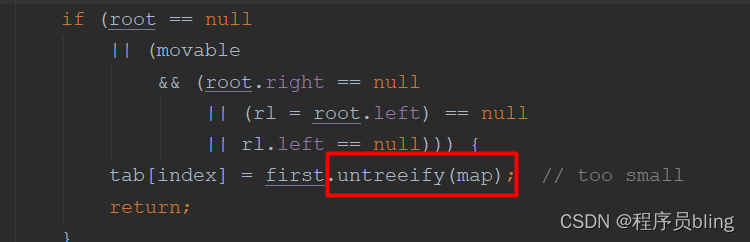
综上:

1. 扩容 resize( ) 时，红黑树拆分成的 树的结点数小于等于临界值6个，则退化成链表。
2. 移除元素 remove( ) 时，在removeTreeNode( ) 方法会检查红黑树是否满足退化条件，与结点数无关。如果红黑树根 root 为空，或者 root 的左子树/右子树为空，或者root.left.left 根的左子树的左子树为空，都会发生红黑树退化成链表。

什么时候会从链表转成红黑树

这里可能有一个误区,就是只要链表长度大于8就会转成红黑树.其实还有一个判断条件.

当链表长度>8并且数组的长度>=64的时候,如果只有链表长度>8但是数组长度小,此时会暂时先进行扩容

小总结

这里我们主要从问题出手, 剖析了HashMap的处理流程, 相信你也收获良多.

在看这个源码的时候,有两点是令我比较惊艳的:

1. 根据巧妙的长度, 利用位运算寻找计算下标,是真的6
2. 还有就是在扩容时,并没有全部重新计算下标, 而是利用规律,通过简单的判断就确认了新下标的位置, 直呼66666

这里再总结一下扩容的过程:

在扩容时,其实主要是针对原数组下标节点进行判断的,主要有以下四种情况:

1. 该下标无节点: 忽略
2. 该下标只有一个节点: 直接重新计算下标,然后赋值
3. 该下标节点包含一个链表:
   这个时候会利用规律,遍历链表上的节点,将其拆分成高位和低位两个链表,然后将两个链表的头节点赋值给新数组即可.
4. 该下标节点包含一个红黑树:
   首先明确这个红黑树上的节点也会最终被分为两拨,高位和低位.
   在hashMap的设计原则中,长度>8才应该是红黑树,所以一个红黑树拆分之后就不一定还是红黑树了,就可能变成链表.
   具体流程如下:
   (1).先拆分成两个链表,
   (2).根据两个链表的长度判断,需要的话将其转成红黑树
   (3).将链表或者红黑树的头结点赋值给新数组

今天的分享就到这里了,有问题可以在评论区留言,均会及时回复呀.
我是bling,未来不会太差,只要我们不要太懒就行, 咱们下期见.