网络分析

来自Manolis Kellis教授（MIT计算生物学主任）的课《人工智能与机器学习》
本节课主要介绍了network和graph的知识
主要内容有网络和图的基础知识（网络类型、相关算法）、网络性质（motifs性质、中心性等）、特征向量、SVD奇异值分解、PCA、Sparse PCA、t-SNE等
我觉得讲的很好！短短一个半小时讲的比我大一学的线性代数有意思多了，很有启发，尽管我的线性代数很烂但不妨碍边学边查最后大概都能听懂。
有需要视频的可以私信发油管链接

1.Introduction to networks and graph foundations and algorithms

Network types (social/bio/comp), Euler/Hamilton, Graphs (matrix/adj)

一些生物网络

1. 调控网络（Regulatory Network）: 这是一个表达基因与其他分子之间关系的网络。这些分子可以调控基因的表达，例如，转录因子（Transcription Factors, TFs）可以结合到特定的基因启动子区域，促使基因表达或抑制基因表达（网络）。
2. 代谢网络（Metabolic Network）: 这是一个描述生物体内各种代谢反应的网络。在代谢网络中，节点代表代谢物（如糖、脂肪酸等），边代表代谢反应，而催化这些反应的酶（Enzymes）通常在边上标注。这个网络可以帮助我们理解生物体内的能量流和物质流。
3. 信号传导网络（Signaling Network）: 信号传导网络描述的是细胞内部以及细胞之间的信号传递过程。例如，细胞膜上的受体蛋白可以接收到外部的信号分子，然后通过一系列的酶反应将信号传递到细胞内部，从而引发细胞的一系列反应。
4. 蛋白质功能相互作用网络（Protein Functional Interaction Network）: 这个网络描绘了蛋白质之间的功能关系。节点代表蛋白质，边代表两个蛋白质之间的功能关系，比如，一种蛋白质可以激活另一种蛋白质的活性。
5. 共表达网络（Co-expression Network）: 在这种网络中，节点代表基因，边代表两个基因的表达模式有相关性。比如，如果两个基因在各种条件下的表达水平都很相似，那么这两个基因就可能在同一个生物过程中发挥作用。

1. Element Identification: 在生物网络中，需要确定的元素可能包括基因、转录因子、代谢物等。比如，你提供的"ATTAAT"和"CGCTT"可能表示在DNA序列中寻找特定的转录因子结合位点（即调控模体，Regulatory Motifs）。
   • Regulators / Regulatory Motifs / Target genes: 在调控网络中，要识别的元素包括转录因子（Regulators），它们通过结合到调控模体（Regulatory Motifs）来调控目标基因（Target genes）的表达。
2. Using networks to Predict expression levels / predict cellular activity / Predict gene ontology (GO) functional annotation terms: 通过分析生物网络，我们可以预测基因的表达水平、细胞的活动状态，以及基因的功能注释（例如，Gene Ontology，GO，它是一个描述基因功能的标准术语体系）。
3. Inferring networks from functional data: 通过分析基因表达数据、蛋白质相互作用数据等功能数据，我们可以推断出生物网络。例如，你提供的"X=f(A, B)"和"Y=g(B)"可能表示的是如何通过数学模型来描述基因或蛋白质之间的交互关系。
   • Activity patterns / Structure / Function: 这些可能是在讨论网络的不同特性，例如，网络中的活动模式（例如，哪些基因同时被激活或抑制），网络的结构（例如，网络中节点和边的分布），以及网络的功能（例如，网络能够完成什么生物过程）。
4. Network Structure Analysis: 分析网络的结构可以帮助我们理解生物过程的组织方式。例如，网络中的Hubs（节点度分布）是那些与许多其他节点相连的节点，这些节点可能在网络中起着关键作用。Network motifs是网络中反复出现的特定模式，它们可能代表某种特定的调控策略。Functional modules则是网络中一组协同工作的节点，它们可能共同参与某个特定的生物过程。

这个领域的挑战可能包括数据的复杂性、不完整性和噪声，计算和存储需求，以及如何从复杂的网络模式中得出生物学上有意义的解释等。

• 与实际相比，网络是一个更加抽象的概念，比如边实际上并不存在，只是表示事物之间的关系，而节点某种意义上只是概率变量
• Edges Represent Relationships Between Data Points： 在更抽象的网络模型中，边可以表示数据点之间的关系。例如，在社交网络中，边可以表示人与人之间的友谊或互动。在物理学中，边可以表示粒子之间的力。在机器学习中，边可以表示样本之间的相似度。此类网络常用于如社交网络分析、系统生物学、推荐系统等领域。
• Nodes as Probabilistic Variables：在最抽象的情况下，节点本身可以被视为概率变量。这种表示在概率图模型中尤为常见，例如贝叶斯网络或马尔可夫随机场中。在这种模型中，每个节点表示一个随机变量，而边表示这些随机变量之间的概率关系。这些网络在各种复杂的预测和推理任务中都有应用，包括自然语言处理、计算机视觉和生物信息学等领域。

1. 物理网络（Physical Networks）: 在这种类型的网络中，边表示节点之间的实际物理交互。例如，在物理调控网络中，边可能代表转录因子（一个蛋白质）与DNA片段之间的物理联系，这种联系可以调控一个或多个基因的表达。这种类型的网络模型通常基于实验数据，如蛋白质-蛋白质相互作用数据或转录因子结合位点数据。
2. 相关性网络（Relevance Networks）: 在相关性网络中，边的权重表示节点间的相似性。例如，在功能调控网络中，如果两个基因在多种环境条件下表达模式相似，它们之间可能存在一条边，且这条边的权重表示它们表达模式的相似性。这种类型的网络模型通常基于计算方法，如相关性计算或互信息计算，而这些计算方法可以应用于各种类型的数据，如基因表达数据或表型数据。

每种类型的网络都有其优点和缺点。物理网络能够提供明确的生物机制信息，但可能因实验技术的限制而不完整或存在偏差。相关性网络可以提供大规模、系统级别的视角，但可能难以解释观察到的模式背后的具体机制。因此，实际的研究往往会结合这两种网络，以获得更全面和准确的理解。

概率网络和图模型是一种利用图形来表示变量间概率关系的方式。这种方法在各种数据分析和机器学习任务中都非常有用。下面是提到的两种类型的概率图模型的介绍：

1. 贝叶斯网络（Bayesian Networks）: 这是一种有向图模型，其中每个节点代表一个随机变量，每条边代表变量间的概率依赖。通常，边从因变量指向结果变量，因此这种网络可以表示为“原因-效果”的关系。例如，如果疾病引起某些症状，那么在贝叶斯网络中，从“疾病”节点到“症状”节点就会有一条边。贝叶斯网络常用于进行因果推断，预测，分类和其他任务。
2. 马尔可夫随机场（Markov Random Fields, MRFs）: 也被称为无向图模型，这是一种无向图模型，其中每个节点代表一个随机变量，每条边代表变量间的概率关系。相比于贝叶斯网络，马尔可夫随机场不强调原因-效果的关系，而是强调变量间的相互关联。例如，如果某个人的社交网络中的朋友们都喜欢某个特定的音乐风格，那么这个人可能也喜欢这个音乐风格。马尔可夫随机场常用于进行结构预测，例如图像分割和图像恢复。

图这个概念更加数学

无向图的Edge，表示是集合

无向图的Edge，表示是元组

用图表示网络，用邻接矩阵表示图

老师这里介绍了邻接矩阵*一个权重向量，类似于权重在图里的扩散，这是从来没有听到过的想法，于是问了问gpt

在图论和网络分析中，矩阵乘法和节点权重的扩散密切相关。为了形象地理解这种关系，让我们考虑一个简单的例子。

假设我们有一个由三个节点组成的网络，我们可以用一个邻接矩阵来表示这个网络，其中的元素表示节点之间的连接。例如，如果节点1和节点2之间有连接，那么在邻接矩阵的第一行第二列处就有一个值。这个值可能是1（表示有连接）或者是其他值（表示连接的强度或权重）。

假设每个节点都有一个权重，我们可以用一个向量来表示这些权重。例如，[w1, w2, w3]。

当我们将邻接矩阵乘以权重向量时，我们就得到了一个新的向量，表示了权重在网络中的扩散或传播。具体来说，新向量中的每个元素是原始权重和邻接矩阵中的相应行的点积（即每个元素相乘后的和）。这就表示了每个节点的权重如何扩散到与其相连的其他节点。

例如，如果节点1的权重是w1，那么在新的权重向量中，节点2的权重将是原来的w2加上邻接矩阵中第二行第一列（表示节点1和节点2的连接）和w1的乘积。这就表示了节点1的权重如何扩散到节点2。

通过这种方式，矩阵乘法可以用来模拟权重在网络中的扩散，这在许多应用中都非常有用，比如在社交网络中模拟信息的传播，或者在生物网络中模拟信号的传播等。

请注意，这里的解释假设了一个简单的线性扩散模型。在更复杂的情况下，扩散模型可能需要考虑其他因素，比如时间延迟、节点的容量限制等。此外，如果网络的连接是有向的，那么在计算新的权重向量时，还需要考虑连接的方向。

可以用邻接列表来表示稀疏矩阵等，更合适

Breadth-first search (shortest paths), Depth-first search (conn. compnts)

2. Emergent global / local network properties in the real world

Global: Small-world, scale-free, clustering, motifs, similarity, dynamics

你提到了几种网络的突现属性，这些属性是由网络的结构和连接方式决定的，而不是由网络的单个节点或边决定的。下面是对你提到的每种属性的解释：

1. 小世界属性（Small-world property）：这种属性描述的是大多数节点可以通过相对较短的路径连接到其他任何节点。这种属性的名字来源于著名的“六度分隔理论”，即任何两个人都可以通过六步或更少的人际关系链找到联系。这种属性的重要性在于，它说明了即使在大型网络中，也可以快速地在节点之间传播信息。
2. 无标度或幂律度分布（‘Scale-free’ or power-law degree distribution）：这种属性描述的是网络中的大多数节点有很少的连接，而少数节点（称为中心或枢纽）有很多连接。这就像是20/80法则，即80%的连接在20%的节点中。这种属性的重要性在于，它可以解释网络的鲁棒性和易受攻击的点，因为枢纽节点在网络中起着重要的作用。
3. 网络增长和优先链接（Network growth and preferential attachment）：这是一个网络动态增长的模型，其中新的节点倾向于链接到已经有较多连接的节点，这就是“富者愈富”的现象。这种模型可以解释为什么网络会呈现出无标度或幂律度分布的属性。
4. 聚集系数（Clustering coefficient）：这个指标衡量了网络中的节点的邻居之间是否也相互连接。换句话说，它度量的是网络中闭合“三角形”（互相连接的三个节点）相对于开放“三角形”（只有两条边的三个节点）的密度。这个指标可以反映网络的聚集程度和社区结构。
5. 网络模式的频率（Frequency of network motifs）：这个指标度量的是网络中某种模式（比如一个特定的子图）出现的频率，比如大小为3，4，5的子图的出现频率。这个指标可以反映网络的复杂性和多样性。

这是老师团队的一个工作：分析网络中的基本组成部分，比如有前馈环（Feed-forward loops）、反馈环（Feedback loops）、交叉调节（Cross-regulation）、**放大（Amplification）**四种类型。在基因里面就是指相互的调控。

网络往往不是随机的

生物网络是生物系统中的各种元素及其相互作用的代表。理解生物网络的属性可以帮助我们理解生物系统的结构和功能。下面是对你提到的一些生物网络属性的解释：

1. 层次结构（Hierarchical organization）：这表示网络中的节点和链接按照不同的层次进行组织。在生物网络中，如基因调控网络，“主调控者”（Master regulators）通常位于层次结构的顶层，控制一系列"局部调控者"（Local regulators）的活动。
2. 度分布（Degree distribution）：这表示网络中节点的链接数量的分布。在许多生物网络中，有一些节点（称为"中心"或"Hubs"）有大量的连接，而大多数节点只有少量的连接。"In-hubs"是指连接大部分入度的节点，"out-hubs"是指连接大部分出度的节点。
3. 直径（Diameter）：这是网络中任意两个节点之间最长最短路径的长度。在生物网络中，直径可以帮助我们理解信息或信号在网络中传播的速度和效率。
4. 信息传递（Info transfer）：这表示信息或信号在网络中的流动方式。例如，信号可能从一个节点传递到另一个节点，或者在网络中的一部分节点之间循环。
5. 模块性（Modularity）：这表示网络可以被划分成多个模块或社区，其中每个模块内部的节点之间的连接密度高于模块之间的连接密度。在生物网络中，模块性可以反映出功能上的区分和专一性。
6. 局部性（Locality）：这表示节点之间的连接主要集中在空间上的相近位置。在生物网络中，空间上相近的节点通常具有相似的功能或属性。
7. 聚类（Clustering）：这表示网络中节点的邻居之间也相互连接的程度。在生物网络中，高度的聚类通常反映了网络的稳定性和鲁棒性。
8. 子网络（Subnetworks）：这表示网络中的一部分节点和连接，它们形成了一个相对独立的系统。在生物网络中，子网络通常对应于特定的生物过程或功能。
9. 流向（Flow direction）：这表示信息或信号在网络中的流向。在生物网络中，流向通常从上游节点向下游节点，例如，从基因到蛋白质。

• 节点性质：中心性

• 节点之间：相似性

一些词语解释：

1. 同配性（Assortative mixing）：这是指具有相似属性的节点更可能相互连接。例如，在社交网络中，人们通常与有相似兴趣或背景的人建立联系。
2. 节点相似性或节点等价性（Node similarity or node equivalence）：有两种基本类型的节点相似性。结构上相似的节点共享许多相同的邻居，而规则上相似的节点则与具有相似属性的邻居共享连接。
3. 属性聚类（Property clustering）：这是指一组节点可以形成一种特定的结构，如团（Clique）、k-plex或k-core，取决于它们之间的连接方式。团是一种所有节点都相互连接的结构，k-plex是一种几乎所有节点都相互连接的结构，每个节点少于k个邻居没有连接，而k-core则是每个节点至少与k个其他节点相连的结构。
4. 定义图邻域的组件（Defining graph neighborhoods with components）：在网络中，一种常见的方式是通过组件来定义节点的邻域或社区。组件是任意两个节点至少通过一条路径相连的节点集合，而k-component则是任意两个节点之间至少有k条独立的路径的节点集合

• 图划分成组件

提到的是关于网络中连接组件和社区检测的一些概念。我将逐一解释：

1. 巨大的连接组件（Giant connected component）：在许多网络中，大部分节点都包含在一个大的连接组件中，即任何两个节点之间都存在至少一条路径。然而，这个大组件内部仍然存在子结构，比如社交网络中的朋友集群。
2. 图划分算法（Graph partitioning algorithms）：这些算法试图将图的节点分割成k个群集，使得群集内部的连接尽可能多，群集之间的连接尽可能少。图划分问题的最简单形式是图二分问题，即将图的节点分成两个等大小的群集，这是一个NP完全问题，只能通过启发式算法进行近似求解。
3. Kernighan-Lin算法：这是一种经典的图划分算法，它先随机将节点分成两个群集，然后反复调整群集的成员，以减小群集之间的连接。
4. 谱划分（Spectral partitioning）：这是一种基于图的拉普拉斯矩阵的图划分方法，它试图将图的节点分成几个群集，使得群集之间的"扩散"（即信息或信号在群集之间的传播）尽可能小。
5. 社区检测算法（Community detection algorithms）：这些算法试图在图中找到一些紧密相连的小群集，也就是社区。常用的社区检测方法有模块度最大化（modularity maximization）、基于谱的方法（spectral methods）、基于介数的方法（betweenness-based methods）等。

1. 渗流和网络韧性（Percolation and network resilience）：渗流理论用于描述网络中的随机过程，比如节点或边的随机移除对网络连接性的影响。这种理论在理解网络的韧性，即网络在面对节点或边的丢失（如路由器故障，网络攻击，或疫苗接种）时能保持多少功能，中非常有用。
2. 网络上的流行病（Epidemics on networks）：在网络上建模疾病的传播可以帮助我们理解疾病如何在人群中传播。在这种模型中，通常假设每个节点（如一个人）可以处于几种不同的状态（如易感状态、感染状态和康复状态），并且随着时间的推移，一个节点的状态可以根据一些规则（如疾病传播率）发生改变。
3. 网络上的动态系统（Dynamical systems on networks）：这涉及到在网络上建模一些时间依赖的过程，如代谢建模或信息流动。这种模型可以帮助我们理解网络中的动态行为，如稳定性、同步性等。
4. 网络搜索（Network search）：网络搜索涉及到在网络中查找特定的信息或节点。在网络搜索中，一个重要的问题是如何设计有效的搜索策略，比如在Web搜索或分布式数据库中，或者在消息传递系统中。

Local: centrality metrics (degree, betweenness, closeness, etc)

前面聊了一些网络的全局属性，现在聊一些网络局部的特性

中间绿色的几个节点，就是高中心性但是度很低，如果要分隔两个网络的话，会选择这几个进行攻击

用于衡量一个节点在网络中的重要性。下面详细解释一下这些概念：

1. 度中心性（Degree Centrality）：对于无向图，节点的度中心性是指它的连接数（即有多少邻居）。在有向图中，我们通常会分别计算入度中心性（有多少节点指向此节点）和出度中心性（此节点指向多少其他节点）。对于加权图，我们可以考虑权重度中心性，即节点连接的权重总和。
2. 介数中心性（Betweenness Centrality）：节点的介数中心性是指所有最短路径中经过该节点的路径的比例。如果一个节点的介数中心性高，那么这意味着在网络中的信息流或任何其他类型的流动中，这个节点具有重要的控制作用。边的介数中心性也是类似定义的，即所有最短路径中经过该边的路径的比例。
3. 接近中心性（Closeness Centrality）：节点的接近中心性是指到网络中所有其他节点的最短路径长度之和的倒数。如果一个节点的接近中心性高，那么这意味着它离网络中的其他节点平均距离较近，因此在传播信息或者影响网络中的其他节点时可能会更有效。
4. 特征向量中心性（Eigenvector Centrality）：它在某种程度上扩展了度中心性的概念，
5. ：一个节点的特征向量中心性等于它的所有邻居的特征向量中心性之和。换句话说，一个节点的重要性不仅取决于它有多少邻居，而且取决于这些邻居的重要性。在数学上，这个定义导致了一个涉及网络邻接矩阵的特征向量的方程。网络的邻接矩阵是一个方阵，其中的每个元素表示一个节点与另一个节点之间的连接。该方程的解就是特征向量中心性。

3. Linear Algebra Review

回顾一下线性代数的一些基础知识

Eigenvector and singular vector decomposition

这里先是从矩阵相乘的操作讲起，从代数层面过渡到了几何层面，引出了SVD奇异值分解（Singular Value Decomposition），然后才讨论特征向量（Eigenvector）

在许多计算科学、数据科学和机器学习问题中，我们经常需要计算矩阵和向量的乘法。例如，给定矩阵A和向量x，我们需要计算y = Ax。这在数学上是非常直观的，但是如果从图形的角度来理解，这个过程可能会有一些新的发现。

首先，我们可以将矩阵A看作是一个图，其中每个节点i对应矩阵的一行，每个边代表该行中的一个元素。向量x可以看作是图中每个节点的初始标签，而向量y则是经过计算后的新标签。

在图的解释中，节点i的新标签y(i)是由其邻居节点的x值（即原标签）乘以对应的边标签（即邻居节点对应的矩阵元素）得到的。这就是矩阵乘以向量的过程，从图的角度看，它是一个权重扩散或信息传播过程。

这个观察结果揭示了一个有趣的事实：密集矩阵和向量的乘法只是稀疏矩阵和向量乘法的特例。在稀疏矩阵中，大部分元素都是零，所以在图中，大部分节点只有少数的邻居。而在密集矩阵中，每个节点都与其他所有节点相连，也就是说，每个节点都从所有其他节点接收信息。所以，从图的角度看，稀疏矩阵和向量的乘法是一种更一般的计算模型，而密集矩阵和向量的乘法只是这个模型的一个特例。

矩阵在转换这个向量

当矩阵乘以一个向量时，我们可以将这个操作看作是一个线性变换。这种线性变换可以被看作是将输入向量映射到新的空间，从而改变其位置或方向。在这个过程中，向量的各个分量与矩阵的各个元素相乘，得到新的向量。这就是所谓的权重扩散。

举个例子，假设我们有一个2维向量v = (v1, v2)，和一个2x2的矩阵A = [[a11, a12], [a21, a22]]。矩阵A乘以向量v的结果是一个新的2维向量w = (w1, w2)，其中w1 = a11*v1 + a12*v2， w2 = a21*v1 + a22*v2。可以看出，新的向量w的各个分量是原向量v的各个分量通过矩阵A的元素加权得到的。

所以，当我们说矩阵乘以一个向量类似于权重的扩散，实际上是说，输入向量的各个分量在变换过程中，被矩阵中的元素加权，形成新的向量。

另外，从高维空间中点的变换的角度理解，这个线性变换就好比是空间中的旋转、缩放、倾斜或者其它形式的几何变换。这个变换会改变向量在空间中的位置和方向，但是会保持一些性质，比如向量的线性关系，即如果一个向量是另外两个向量的线性组合，在变换后，这个关系仍然保持。所以矩阵和向量的乘法，可以看作是在高维空间中进行几何变换。

• SVD奇异值分解

线性代数中的矩阵运算可以在几何上得到解释。以下是对剪切（Shearing）、旋转（Rotation）和缩放（Scaling）这三种矩阵运算的几何解释：

1. 剪切（Shearing）：在二维空间中，剪切变换会改变物体的形状，但不会改变其面积。对于给定的向量，其在某个方向（比如x方向）的坐标将会增加其在另一个方向（比如y方向）坐标的倍数。剪切矩阵有一个非对角线元素，例如

   [1, a]
   [0, 1]
   

   这个矩阵将y方向上的移动转化为x方向上的移动。

2. 旋转（Rotation）：旋转变换会使物体在平面上围绕某个点旋转一定的角度，但不会改变其形状和大小。在二维空间中，旋转矩阵可以用角度θ来表示：

   [cosθ, -sinθ]
   [sinθ, cosθ]
   

   这个矩阵将向量旋转θ角度。

3. 缩放（Scaling）：缩放变换会改变物体的大小，但不会改变其形状。在二维空间中，缩放矩阵是一个对角矩阵，可以用缩放因子a和b来表示：

   [a, 0]
   [0, b]
   

   这个矩阵将x方向上的长度放大a倍，将y方向上的长度放大b倍。

这里就很强大了，为什么呢，因为$\sum$是一个对角矩阵，其对角上的每一个值，表示每一个维度的缩放大小。然后U和V就是简单的旋转（不改变大小）

同样的，我们可以把M*x看作一个函数，函数就是先对x乘V*（旋转），然后S（缩放），最后U（旋转）。就相当于乘M矩阵的效果

因为本人的线性代数基础不是很好，SVD分解也不是三言两语就能说明白的，所以这里需要自行学习（日后我进一步理解了，也会回来补充）

---

在有了上述这些操作（剪切、旋转、缩放）的时候，老师才开始讲什么是特征向量。

这里举了一个例子，M为矩阵$$\begin{array}{cc}6& -2\\ 4& 0\end{array}$$，x为$$\begin{array}{c}1\\ 2\end{array}$$，二者相乘就相当于对x进行了一系列的操作（旋转、缩放、再旋转），但结果等价于对x进行了一个简单的线性变换（2*x）。

这个理解很amazing，也就是说在M对空间进行重塑的时候，这个x是不变的

by gpt4 :

在几何意义上，矩阵A的特征向量就是在A的线性变换下，其方向保持不变（可能会翻转），只是长度发生缩放的向量。这个缩放的因子就是对应的特征值。也就是说，如果v是矩阵A的一个特征向量，λ是对应的特征值，那么Av=λv，也就是说，线性变换A作用在特征向量v上，等同于把v沿着自身的方向拉伸或压缩λ倍。

举个简单的例子，考虑二维空间中的一个线性变换，用2x2矩阵表示。如果这个矩阵有两个线性无关的特征向量，那么它们就分别沿着x轴和y轴。对于沿着x轴的特征向量，线性变换可能会将其拉伸或压缩，但方向保持不变；对于沿着y轴的特征向量，同样的事情发生。这种变换的效果就是将整个空间拉伸或压缩，但不会改变空间的方向。

对于一个m*m的矩阵，有多少个对应的特征向量的讨论：

把矩阵看作一个个列向量，如果这些向量在空间里都不是平行的，那就会有m个特征向量，如果有平行的（线性相关），那就<m个

by gpt4 :

一个 m*m 的矩阵的特征向量的数量取决于矩阵的特性。理论上，一个满秩的 m*m 矩阵可以有最多 m 个线性无关的特征向量。这些特征向量可以构成该矩阵所在空间的一个基。

然而，具体的数量可能会少于 m。这主要是因为一个特征值可能对应着多个线性相关的特征向量，或者称为特征空间。例如，如果一个矩阵的两个特征值相同，那么它可能只有一个线性无关的特征向量，因为这两个特征值对应的特征向量可能是线性相关的。

另外，如果一个矩阵不是满秩的，那么它可能没有 m 个线性无关的特征向量。例如，如果一个矩阵是奇异的（即其行或列线性相关），那么它可能只有少于 m 的特征向量。

总的来说，一个 m*m 的矩阵的特征向量的数量取决于其特征值的数量（包括重复的）以及每个特征值对应的特征向量的线性无关性。

用一个例子来表示矩阵向量乘法和特征向量/特征值的关系，这里解释一下：

首先，给出的矩阵S有三个特征值：3, 2, 0，对应的特征向量分别为v1, v2, v3。矩阵S在每个特征向量上的作用可以看作是一个恒等变换，但在每个特征向量上的放大倍数（即特征值）是不同的。

然后，给出了一个向量x，它可以被表示为这三个特征向量的线性组合：x = 2v1 + 4v2 + 6v3。当我们对x进行矩阵S的线性变换时，因为v1, v2, v3是S的特征向量，所以每个v都只会被各自对应的特征值放大，不会改变方向。

这就意味着**，如果我们先对x做矩阵S的线性变换，再将其表示为v1, v2, v3的线性组合，结果将会等同于先将x表示为v1, v2, v3的线性组合，再对每个v分别做S的线性变换。**这就是矩阵和特征向量/特征值在几何上的意义。

对于复杂的矩阵变换问题，我们通常希望能找到这样的一组基（即特征向量），使得在这组基上的变换可以简化为对角矩阵，也就是说，每个基向量只会被各自对应的特征值放大，不会相互影响。这就是特征向量和特征值在解决实际问题中的价值。

上面加粗的字，是重点，简单来说，就是本来S*x是一系列复杂的变换，但x能表现为v1, v2, v3（S的特征向量）的线性组合(比如x = 2v1 + 4v2 + 6v3)，所以S*x =2S*v1+4S*v2+6S*v3。

因为特征向量，矩阵*特征向量=特征值*特征向量，这个就非常简单了，乘一个标量就完事了，于是S*x =2*3*v1+4*2*v2+6*0*v3=6v1+8v2

这个例子也揭示了“小”特征值的影响是有限的。在上面的例子中，因为第三个特征值为0，所以S对应于该特征值的特征向量v3的作用实际上是没有效果的：Sv3 = 0v3 = 0。这就说明，如果一个矩阵的一个特征值非常小，那么对应于这个特征值的特征向量在矩阵变换下的影响将会非常有限。反之，如果特征值较大，那么对应的特征向量在矩阵变换下的影响就会相对更大。这也是为什么在一些问题中，如主成分分析（PCA）等，我们往往只关注那些具有较大特征值的特征向量，因为它们在矩阵变换下的影响较大，包含了主要的信息。

• 前面是提到了奇异值分解（更一般的情况），在S的所有特征值都是实数且S有m个线性独立的特征向量时，我们就有特征值分解（特殊的情况）

对于一个矩阵S，如果它有m个线性独立的特征向量（也就是说，矩阵是非退化的），那么就存在一个特征值分解（或者说对角化）：S = UAU^-1。

在这个分解中：

• U是一个m x m的矩阵，它的列就是S的特征向量v1, v2, …, vm。这些特征向量通常被归一化，使得它们的长度（或者说范数）为1。
• A是一个m x m的对角矩阵，它的对角线上的元素就是S的特征值λ1, λ2, …, λm。这些特征值对应于U中的特征向量。
• U^-1是U的逆矩阵。

这个分解告诉我们，任何一个非退化的矩阵S都可以被表示为其特征向量构成的矩阵U、一个对角矩阵A和U的逆矩阵的乘积。这个分解在许多应用中都非常有用，例如在解决线性微分方程、对矩阵进行简化计算、数据降维（如PCA）等问题时。

关于Eigen/diagonal Decomposition和Singular Value Decomposition的区别和联系（by gpt4）：

特征值分解和奇异值分解（SVD）都是将矩阵分解为较简单矩阵的乘积的方法，但它们适用于不同的情况，有着不同的性质。

特征值分解

特征值分解适用于方阵，即行数和列数相同的矩阵。当一个矩阵有n个线性无关的特征向量时，就可以被特征分解为：

A = QΛQ^−1

其中Q是一个由特征向量组成的矩阵，Λ是一个对角线上是特征值的对角矩阵。需要注意的是，并非所有方阵都可以被特征分解，例如那些没有n个线性无关特征向量的矩阵。

奇异值分解

奇异值分解更为通用，适用于任何m×n的矩阵，不限于方阵。任何矩阵A都可以被分解为：

A = UΣV^T

其中U和V是正交矩阵，Σ是一个对角线上元素为非负的对角矩阵，对角线上的元素称为奇异值。

区别和联系

1. 特征值分解只适用于方阵，而奇异值分解适用于任何矩阵。
2. 特征值分解需要矩阵具有n个线性无关的特征向量，而奇异值分解对矩阵没有这个要求。
3. 特征值分解中的特征向量并非总是正交的，而奇异值分解中的U和V矩阵的列向量总是正交的。
4. 奇异值分解的奇异值总是实数且非负的，而特征值分解的特征值可以是任何复数。
5. 两种分解都能提供矩阵的重要信息。例如，特征值和特征向量可以告诉我们线性映射的“拉伸”和“旋转”方向，而奇异值分解的奇异值则给出了矩阵的主要“能量”方向。
6. 如果矩阵A是实对称矩阵，那么特征值分解和奇异值分解是等价的。在这种情况下，特征值和奇异值都是实数，特征向量和左/右奇异向量是相同的

4. Sparse Principal Component Analysis

PCA

矩阵的奇异值实际上是变化的主成分

奇异值分解（SVD）和主成分分析（PCA）都是线性降维的方法，能够在保留主要信息的同时减小数据的维度。两者有紧密的联系，实际上，PCA可以通过SVD来进行计算。

主成分分析的目标是找到一组正交基，使得数据在这组基上的投影方差最大。这组基被称为主成分。PCA通常应用于协方差矩阵，而协方差矩阵是对称正定的，可以进行特征值分解。特征值分解后，特征值大的对应的特征向量即为主成分。

然而，SVD是对任意矩阵进行的分解，可以将任意矩阵分解为UΣV^T的形式。在SVD中，左奇异向量U对应了原始数据的基，右奇异向量V对应了投影空间的基，奇异值Σ则给出了在这些基上的坐标。这和PCA很类似：PCA的主成分对应于SVD的右奇异向量，而PCA的得分（也就是数据在主成分上的坐标）对应于SVD的奇异值。

这就是为什么说奇异值实际上是变化的主成分：奇异值给出了在主成分上的坐标，而这些坐标代表了数据在这些方向上的变化量。一个大的奇异值对应了一个主要的变化方向，而一个小的奇异值则对应了一个次要的变化方向。因此，通过保留大的奇异值和对应的奇异向量，我们可以在保留数据主要变化方向的同时降低数据的维度。

举一个例子，同一个数字其主成分，在空间中是相互靠近的：

MNIST（Modified National Institute of Standards and Technology）手写数字数据集是一个非常流行的图像识别数据集，包含了0到9这10个数字的灰度手写数字图片。这个数据集的每一个样本是一个28x28像素的图像，即784维的数据。

当我们对这样一个高维数据进行分析或建模时，会面临计算量大、数据稀疏等问题。因此，需要对数据进行降维处理，而PCA（主成分分析）是一种常用的降维方法。

在对MNIST数据集进行PCA处理的时候，会首先计算出所有样本在784维空间的协方差矩阵，然后对这个协方差矩阵进行特征值分解。由于协方差矩阵是对称的，所以可以得到一组正交的特征向量，这些特征向量就是主成分。

特征值代表了对应的主成分在原始数据中的重要程度，特征值越大，代表对应的主成分越重要。通过选择前k个最大特征值对应的特征向量，我们就可以得到一个k维的新空间，然后将原始的784维数据投影到这个k维空间中，就完成了降维。

在PCA处理后的MNIST数据中，每一张手写数字的图片都被表示为k维的向量。这个k维的向量就是原始784维图片在k个主成分上的坐标。这样就大大降低了数据的维度，同时还尽可能保留了原始数据的重要信息

Sparse PCA

PCA (Principal Component Analysis) 和 SPCA (Sparse Principal Component Analysis) 是机器学习和统计分析中用来降维的技术，它们的目标是将高维数据转换到一个低维的空间中，同时保留数据中的主要变化模式或结构。

PCA的工作原理是找到数据中的主成分，这些主成分是数据中的方差最大的方向。具体来说，第一个主成分是数据方差最大的方向，第二个主成分是与第一个主成分正交且具有最大方差的方向，以此类推。通过将数据投影到这些主成分所定义的空间中，PCA可以降低数据的维度。

PCA能够减少数据中的冗余或者依赖性，是因为它将数据转换到新的坐标系中，在这个坐标系中，各个主成分之间是线性无关的，也就是说，它们是正交的。这样，PCA可以去除原始数据中的冗余信息，从而达到降维的目的。

然而，PCA的一个缺点是，所有的主成分都是原始特征的线性组合，这使得PCA产生的结果往往难以解释。Sparse PCA 是为了解决这个问题而提出的。与PCA不同，Sparse PCA试图找到一个主成分向量，这个向量在大多数维度上为零，只在少数几个维度上有非零值。这样，Sparse PCA产生的主成分就更容易理解，因为它们只涉及原始特征的一个小子集。

总的来说，PCA和Sparse PCA都是用来降维和减少数据中的依赖性的技术，它们通过找到数据的主成分并将数据投影到主成分所定义的空间来实现这个目标。PCA适用于那些我们希望最大化方差和去除冗余的情况，而Sparse PCA则更适合那些我们希望得到易于解释的主成分的情况

L1/L2 regularization

Sparse PCA的实现通常需要使用一种称为lasso（Least Absolute Shrinkage and Selection Operator）的技术。lasso是一种用于线性回归的正则化方法，它可以将回归系数向量的一部分元素压缩到零，从而达到特征选择的目的。通过在PCA的优化问题中引入lasso正则化，我们可以得到Sparse PCA。

L1和L2正则化是用于防止机器学习模型过拟合的技术。它们通过在模型的目标函数中添加一个正则化项（即模型参数的L1或L2范数）来实现这一目标。L1正则化可以使一些参数变为零，从而实现特征选择。L2正则化会让模型参数趋向于小值，防止模型过于复杂。

PCA和正则化在一些情况下可以结合使用。例如，你可以先使用PCA降低数据的维度，然后在降维后的数据上训练一个使用L1或L2正则化的模型。这种方法可以帮助你处理高维数据，并防止模型过拟合。

Non-linear embeddings

这里懒得摘录ppt了，老师翻的太快，前面所说的PCA都是线性降维的技术，是改变了空间。而也有非线性降维的技术，是通过点的邻居（数据点之间的概率相似度）来做的，那就是t-SNE。(原理就不过多介绍了)

b站学习链接：python与人工智能-数据降维-t-SNE

t-SNE，全称为t-Distributed Stochastic Neighbor Embedding，是一种机器学习算法，主要用于高维数据的可视化。特别地，它被广泛应用于将多维数据集减少到二维或三维，从而可以在平面或三维空间中进行可视化。

t-SNE的工作原理概括如下：

1. 计算高维空间中的数据点之间的概率相似度。在此步骤中，t-SNE使用高斯分布计算两个点在高维空间中的相似度。
2. 计算低维空间中的数据点之间的相似度。t-SNE使用一个叫做t分布（其实是Student’s t分布的一种形式）来计算低维空间中的相似度。
3. 优化过程。t-SNE使用一种叫做KL散度的度量方式，来最小化高维空间和低维空间中的相似度之间的差异。这是一个非线性的优化过程。

t-SNE的一个重要优点是，它能够保留数据中的局部结构，并且在一定程度上也能够保留全局结构。这意味着相似的数据点在低维空间中将会紧密地聚集在一起。

然而，t-SNE也有其局限性。例如，它的计算复杂度相对较高，对于大规模数据集可能需要较长的计算时间。此外，t-SNE的结果也受到一些超参数（例如 perplexity 和 learning rate）的影响，可能需要通过多次尝试来找到合适的参数设置。

PCA和t-SNE都是数据降维的技术，但它们的方法和优点是不同的。

PCA是一种线性降维技术，它的目标是找到数据的主要变化方向，这些方向被称为主成分。PCA试图保留数据中的最大方差，并将数据投影到由主成分定义的新的低维空间。因此，PCA通常更好地保留了数据中的全局结构，但可能在保留数据中的局部结构方面效果不佳。

与此相反，t-SNE是一种非线性降维技术，主要侧重于保留数据中的局部结构。t-SNE试图保留距离较近的点之间的相似度，并使用随机梯度下降方法来寻找最佳的低维表示。因此，t-SNE通常能够很好地保留数据的局部结构，但可能在保留全局结构方面效果不佳。

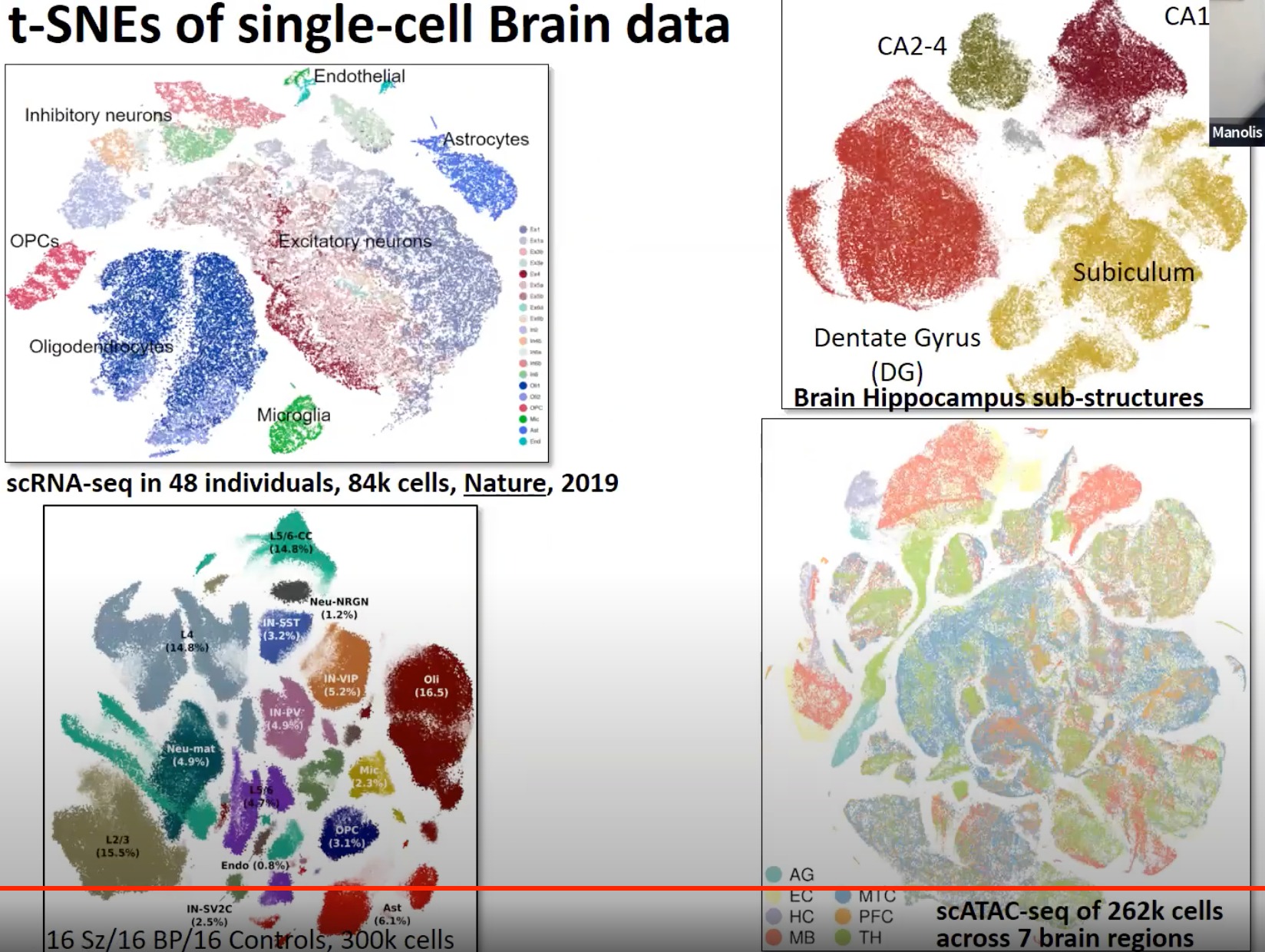
• t-SNE同样的手写数字识别的数据集，可以看出跟前面PCA的效果区别还是很明显的。t-SNE更多的是关注局部

• 在生物信息里的应用
  • 单细胞RNA测序数据可视化：t-SNE被广泛应用于单细胞RNA测序数据的降维和可视化。通过使用t-SNE，研究者可以将每个细胞的基因表达模式映射到二维或三维空间，并进一步识别出不同的细胞群落。
  • 蛋白质表达数据分析：t-SNE也可以用于分析蛋白质表达数据，以帮助研究者识别蛋白质表达模式和功能群组。
  • 疾病分类和药物反应预测：t-SNE可以帮助研究者理解疾病的生物学基础，通过将患者的基因表达模式映射到低维空间，研究者可以更好地区分不同类型的疾病，或预测患者对特定药物的反应。

还剩下以下板块没时间讲，俺有时间再补(主要涉及内容：拉普拉斯矩阵、谱聚类、Guilt by association、网络扩散核Network Diffusion Kernels、随机游走等)

• Network Communities and Modules
  • Guilt by association
  • Maximum cliques, density-based modules and spectral clustering
• Network Diffusion Kernels and Deconvolution
  • Network diffusion kernels
  • Network decorvorution

网络社区和模块

网络社区和模块指的是网络中的节点群组，它们与群组内的其他节点的连接比与网络其余部分的连接更为紧密。识别这些结构是网络分析的重要任务，因为这可以帮助理解网络所代表的系统的底层机制。

例如，在蛋白质-蛋白质相互作用网络中，密集连接的社区可能代表蛋白质复合物或功能单元。同样，在社交网络中，社区可能代表朋友群或有相似兴趣的人。

罪恶关联 Guilt by association

"罪恶关联"是生物学中常用的概念，表示相互关联或相互作用的基因（或蛋白质）可能参与同一生物过程。因此，如果一个未知功能的基因经常与已知功能的基因相关联，可以推断该未知基因也可能参与该功能。

最大团，基于密度的模块和谱聚类

这些都是用来识别网络中社区或模块的方法：

• 网络中的一个团是一组节点的子集，这些节点中的任意两个节点都相互连接。最大团是网络中最大的团。
• 基于密度的模块指的是子网络，其中内部连接密度（实际连接与潜在连接的比率）高。
• 谱聚类是一种使用网络的拉普拉斯矩阵的特征向量来聚类节点的技术。

网络扩散核和反卷积

网络扩散核代表了网络中两个节点之间的随机游走的可能性。它们可以捕获网络的连接结构，并可以用于节点分类或链接预测等任务。

网络反卷积是一种用于移除网络中间接关联（即，两个节点之间的关联是由于它们都与第三个节点连接而产生的关联）的方法，以突显直接连接。