39. 组合总和

思路

我举过例子，如果是一个集合来求组合的话，就需要startIndex，例如：77.组合，216.组合总和III 。

如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：17.电话号码的字母组合

剪枝优化：对于sum已经大于target的情况，其实是依然进入了下一层递归，只是下一层递归结束判断的时候，会判断sum > target的话就返回。
其实如果已经知道下一层的sum会大于target，就没有必要进入下一层递归了。
那么可以在for循环的搜索范围上做做文章了。
对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。

代码

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startidx) {
        if(sum > target) return;

        if(sum == target) {
            result.push_back(path);
            return;
        }

        for ( int i = startidx; i < candidates.size(); i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates,target,sum,i);
            sum -= candidates[i];
            path.pop_back();
        }
        
    }

public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        result.clear();
        path.clear();
        backtracking(candidates,target,0,0);
        return result;
    }
};

总结

在求和问题中，排序之后加剪枝是常见的套路！

40.组合总和II

思路

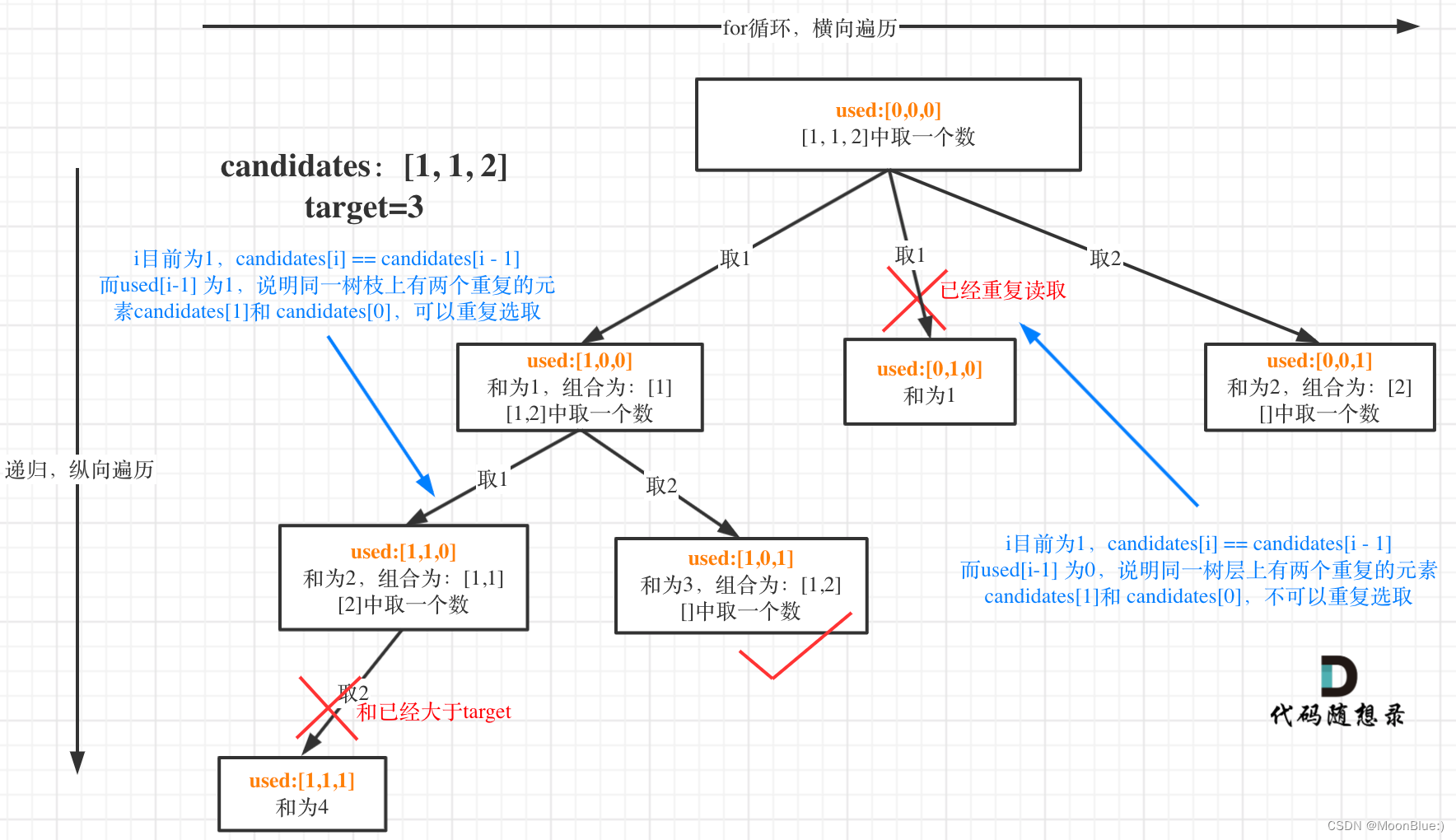
树层去重的话，需要对数组排序！
在这里插入图片描述

代码

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startidx, vector<bool>& used ) {
        if(sum > target) {
            return;
        }
        if(sum == target) {
            result.push_back(path);
            return;
        }

        for(int i = startidx; i < candidates.size() && sum + candidates[i] <= target; i++) {
            if(i>0 && candidates[i] == candidates[i-1] && used[i-1] == false) {
                continue;
            }

            sum += candidates[i];
            used[i] = true;
            path.push_back(candidates[i]);
            backtracking(candidates,target,sum,i+1,used);
            // 回溯
            sum -= candidates[i];
            used[i] = false;
            path.pop_back();
        }

    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        result.clear();
        path.clear();
        vector<bool> used(candidates.size(),false);

        // 要先排序，让相同的元素挨在一起
        sort(candidates.begin(),candidates.end());

        backtracking(candidates,target,0,0,used);
        return result;
    }
};

总结

直接用startIndex来去重也是可以的，就不用used数组了。剩下一个数组的空间
注意排序
树层去重与树枝去重的区别

131.分割回文串

思路

切割问题，有不同的切割方式
判断回文

切割问题实际上也是一种组合问题

回文问题的优化：给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。
大家如果熟悉动态规划这种算法的话, 我们可以高效地事先一次性计算出, 针对一个字符串s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤
优化后的回文判断方法代码：

 void computePalindrome(const string& s) {
        // isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串 
        isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小
        for (int i = s.size() - 1; i >= 0; i--) { 
            // 需要倒序计算, 保证在i行时, i+1行已经计算好了
            for (int j = i; j < s.size(); j++) {
                if (j == i) {isPalindrome[i][j] = true;}
                else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}
                else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}
            }
        }
    }

代码

class Solution {
private:
    vector<vector<string>> result;
    vector<string> path;

    void backtracking (string s, int startidx) {
        if(startidx >= s.size()) {
            result.push_back(path);
            return;
        }

        for(int i = startidx; i < s.size(); i++ ){
            if(isPalindrome(s,startidx,i)) {
                string str = s.substr(startidx, i - startidx + 1);
                path.push_back(str);
            }
            else {
                continue;
            }

            backtracking(s,i+1);
            path.pop_back();
        }
    }

    bool isPalindrome(string& s, int start, int end) {
        for ( int i = start, j = end; i < j; i++, j--) {
            if(s[i] != s[j]) {
                return false;
            }
        }
        return true;
    }
public:
    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        backtracking(s,0);
        return result;
    }
};